9.7. Собственные векторы линейного оператора
В векторном пространстве V над произвольным полем P задан линейный оператор .
Определение 9.13. Ненулевой вектор x называется собственным вектором линейного оператора с собственным значением λ, если (х) = λx.
Говорят, что вектор x принадлежит собственному значению λ.
При этом λ называется не только собственным значением вектора x, но и собственным значением линейного оператора .
Пример 9.5. 1) Любой ненулевой вектор является собственным вектором оператора гомотетии.
2) Рассмотрим оператор дифференцирования в пространстве дифференцируемых функций. Вектор f = е3х является собственным вектором этого оператора с собственным значением 3, так как f ' = 3е3х = 3f.
3) Для
линейного оператора, заданного матрицей
M() = 
собственным
является
вектор
c = (1,
2, 0), так как (с) = 2с.
Проверим это:
[(с)] = M()[c] = 
= 
= 2
= 2[с].
9.7.1. Свойства собственных векторов
1. Каждый собственный вектор принадлежит только одному собственному значению.
Доказательство. Пусть x собственный вектор с двумя собственными значениями 1 и 2. Тогда (x) = 1х и (x) = 2x. Отсюда 1х = 2x (1 – 2)x = 0 и так как вектор x ненулевой, то (1 – 2) = 0 1 = 2.
2. Если вектор x – собственный вектор линейного оператора с собственным значением λ, то вектор y = kx (k 0) тоже собственный с тем же собственным значением λ.
Доказательство. (y) = (kx) = k(x) = k(x) = (kx) = y. Следовательно, вектор y – собственный вектор оператора с собственным значением .
3. Множество собственных векторов с одним и тем собственным значением λ при добавлении нулевого вектора образует подпространство пространства V.
Доказательство. Обозначим это множество символом L(). Докажем, что множество L() {o} образует подпространство пространства V, для чего проверим его замкнутость относительно сложения векторов и умножения их на элемент поля.
Пусть x, y L() {o}, тогда (x) = х, (y) = y. Найдем (x + y): (x + y) = (x) + (y) = х + y = (х + y), значит (х + y) L() {o}.
Пусть x L() {o}, k P, (x) = х, тогда (kx) = k(x) = k(х) = (kх), значит kх L() {o}.
4. Собственные векторы с попарно различными собственными значениями линейно независимы.
Следствие. Линейный оператор, заданный в n-мерном линейном пространстве, не может иметь более чем n различных собственных значений.
9.7.2. Характеристический многочлен матрицы
Дана матрица A Рnn (или A Rnn).
Определение 9.14. Характеристическим многочленом матрицы A называется многочлен, зависящий от λ и равный |A – E|, т. е. многочлен f(λ) = |A – E|, где E – единичная матрица таково же порядка что и А.
Пример 9.6.
Найти
характеристический
многочлен матрицы
A =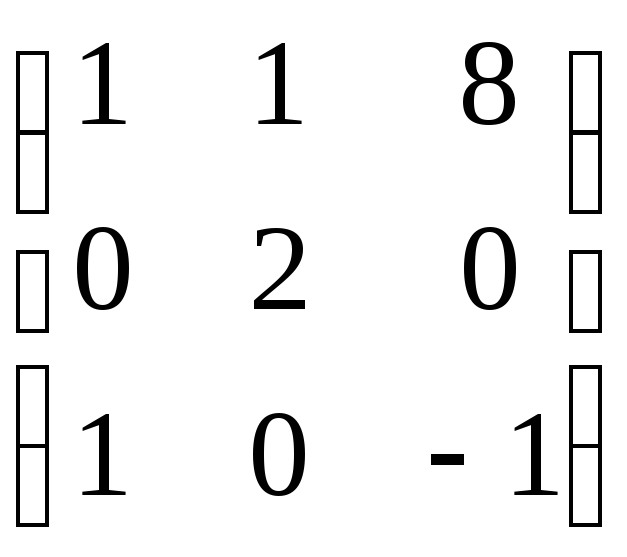 
.
Решение. Составим определитель матрицы A – E и вычислим его
|A – E| = 
= 
=
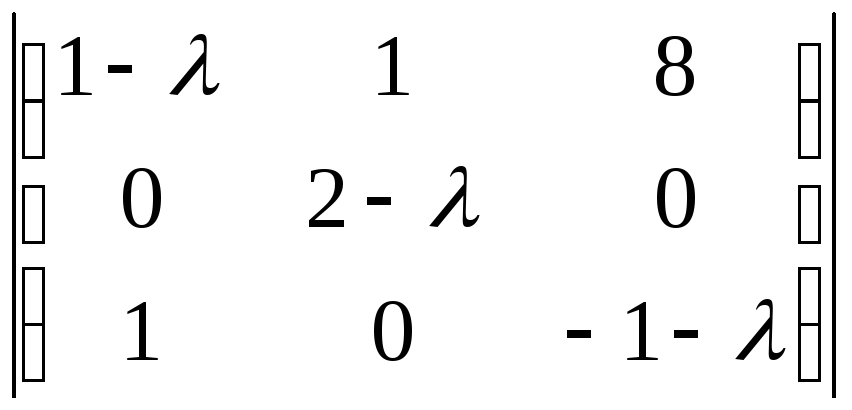= (2 – λ)(–1)2 + 2
·
= (2 – λ)((1 – )(–1 – ) – 8) =
= (2 – λ)(λ – 3)(λ + 3).
Определение 9.15. Характеристическим уравнением матрицы A называется уравнение |A – E| = 0.
Определение 9.16. Собственными значениями (собственными числами) матрицы A называются корни ее характеристического уравнения.
Найдем собственные значения матрицы из примера 9.6: (2 – λ)(λ – 3)(λ + 3) = 0. Получим: 1 = 2, 2 = 3, 3 = –3.
Теорема 9.12. Характеристические многочлены подобных матриц равны.
Доказательство. Пусть матрицы А и В подобны, то есть А = T –1ВТ. Тогда
|A – E| = |T –1ВТ – T –1ЕТ | = |T –1(В – Е)Т | = |T –1||В – Е||Т | = = |T –1||Т ||В – Е| = |T –1Т ||В – Е| = |E||В – Е| = 1|В – Е| = |В – Е|.
Так как характеристические многочлены равны, то совпадают и множества собственных значений подобных матриц А и В.
Следствие. Характеристический многочлен матрицы линейного оператора не зависит от базиса, в котором найдена эта матрица (матрицы линейного оператора, найденные в различных базисах, подобны).