2. КВАНТОВОЕ ОПИСАНИЕ РАССЕЯНИЯ

2.1 Пределы классического описания

Приведенное в Приложении классическое описание процесса рассеяния в терминах частиц и траекторий движения является очень наглядным и справедливым во многих ситуациях как для нерелятивистских, так и релятивистских частиц. В обоих случаях конечная судьба частиц после столкновения определяется потенциалом взаимодействия, начальным импульсом налетающей частицы и прицельным расстоянием, которые однозначно задают траектории движения. Неоднозначность появляется только для пучка частиц, что и приводит к понятию о дифференциальном сечении рассеяния. Из квантовой механики известно, однако, что при определенных условиях знакомые понятия частиц, траекторий движения и прицельных расстояний следует видоизменить, чтобы учесть волновые свойства частиц. Приведенное в предыдущих разделах описание рассеяния оправдано в тех случаях, когда можно пренебречь влиянием квантового принципа неопределенности. Общие методы квантовой теории позволяют исследовать процесс рассеяния и в тех случаях, когда волновые свойства частиц начинают играть существенную роль. Замечательной особенностью квантовой теории рассеяния является то, что изменяется только метод расчета физических величин, например, дифференциальных и полных сечений, в то время как само понятие дифференциального сечения имеет тот же смысл, что и в классической физике.

С учетом волновых свойств частиц необходимо сразу ответить на вопрос о том, когда можно пренебречь влиянием принципа неопределенности и при выполнении каких условий остается применимым классическое описание, приведенное в предыдущих разделах. Как известно, только для идеальной плоской волны, существующей с равной вероятностью во всем

пространстве, можно однозначно задать некоторый волновой	вектор k и
вектор импульса p = k . Во всех остальных практически	реализуемых

ситуациях частицу приходится рассматривать как волновой пакет, содержащий компоненты с разными волновыми векторами и частотами. Под скоростью частицы v в этом случае подразумевают групповую скорость распространения всего пакета волн. Согласно принципу неопределенности ширина такого пакета ∆x в некотором выделенном направлении x связана с

разбросом импульсов составляющих его волн ∆px	в этом же направлении
соотношением
∆x∆px ≥ .	(2.1)

Аналогично классическому, при квантовомеханическом описании столкновений можно ввести относительную систему отсчета. Рассеяние

∆x }∆px

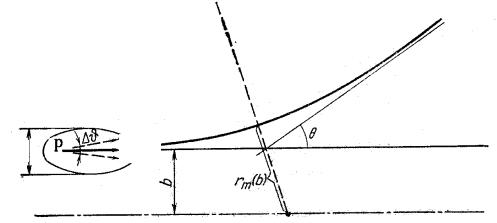
Рис.2.1 Условная пространственная конфигурация волнового пакета и неподвижногоцентрарассеяниявотносительнойсистемеотсчета

волнового пакета в относительной системе отсчета, для которой центр рассеяния неподвижен и p = µv , схематически изображено на рис.2.1.

Возможность квазиклассического описания рассеяния с использованием представления о налетающей частице с определенным прицельным расстоянием b и импульсом p должна формулироваться в виде условий для

обоих этих параметров.

Понятно, что о прицельном расстоянии можно говорить только в том случае, если поперечные размеры пакета волн существенно меньше некоторого характерного размера рассеивающего центра. В противном случае никогда нельзя сказать (с большей или меньшей определенностью), на каком расстоянии от центра рассеяния пролетает частица. В качестве такого параметра, характеризующего эффективные поперечные размеры рассеивателя при заданном прицельном расстоянии частицы, можно выбрать расстояние максимального сближения rm :

∆x << rm (b, Eотн ) .

(2.2)

При необходимости условию (2.2) всегда можно удовлетворить экспериментально соответствующим выбором пучка частиц с определенными волновыми свойствами.

В соответствии с соотношением неопределенностей (2.1) ограничение (2.2) для волнового пакета в пространстве можно записать в виде ограничения на неопределенность в распределении поперечного импульса в волновом пакете:

	∆p		≥		>>				.	(2.3)
		x		∆x		r (b, E	отн	)
						m

С другой стороны, неопределенность импульса (2.3) означает, как видно из рис.2.1, изначальную угловую неопределенность ∆ϑ в направлении распространения падающих частиц, поэтому

∆ϑ ≈ tg∆ϑ =	∆px >>				.	(2.4)
		pr (b, E		)
	p		отн
		m

Здесь фактически предполагается, что неопределенность угла мала.

Легко видеть, что о рассеянии частиц в его классическом понимании и об асимптоте траектории движения с заданным углом рассеяния ϑ имеет смысл говорить только тогда, когда этот угол существенно больше первоначальной неопределенности углов в направлении распространения падающих частиц:

	ϑ >> ∆ϑ ≈	∆px	(2.5)
		p

Условие (2.5) на импульсы частиц совместно с неравенством (2.4) приводит к окончательному условию справедливости квазиклассического рассмотрения процессов рассеяния:

				<<ϑ .	(2.6)
pr	(b, E	отн	)
m

Если критерий применимости (2.6) выполняется в относительной системе отсчета, то можно воспользоваться известными соотношениями, связывающими углы рассеяния и импульсы частиц в лабораторной системе отсчета с p и ϑ , и получить аналогичный критерий квазиклассичности

рассеяния в лабораторной системе отсчета. В частности, из выражения (П.37) следует, что при не слишком больших углах рассеяния ϑ <1 в соотношении

(2.6) можно произвести простую замену импульсов и углов p и ϑ на p1 и ϑ1 независимо от соотношения масс сталкивающихся частиц. Иными словами, если при ϑ <1 условие (2.6) квазиклассического описания выполняется в

относительной системе отсчета, то в лабораторной системе отсчета оно будет справедливым для импульса p1 и угла рассеяния ϑ1 . Отметим также, что угол

рассеяния ϑ можно выразить и через энергию E2′, передаваемую частице-

мишени в лабораторной системе отсчета, тогда из условия (2.6) получается интервал энергий отдачи, для которого справедливо классическое описание.

Неравенство (2.6) можно переписать также, используя де-бройлевскую длину волны = 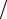p относительного движения:

			<<ϑ .	(2.7)
r (b, E	отн	)
m

Неравенство (2.7) имеет прозрачный физический смысл. Если де-бройлевская длина волны частицы мала по сравнению с размерами препятствия, то рассеяние только для очень малых углов нельзя рассматривать классически (для таких углов всегда будут иметь место дифракционные явления, которые нужно учитывать). В электродинамике подобная квазиклассическая ситуация при рассеянии электромагнитных волн называется приближением геометрической

оптики. В обратном предельном случае пренебречь волновыми эффектами нельзя ни для каких углов рассеяния.

Из двух величин ϑ и b в неравенстве (2.7) в качестве независимой переменной можно выбрать любую, поскольку они связаны соотношением (П.24). Поэтомусловияу (2.6) и (2.7) представляют собой ограничение либо на углы рассеяния, либо на прицельные расстояния, для которых применимо классическое описание. С помощью формулы (П.24), дающей явную зависимостьϑ =ϑ(b, Eотн ) , из условия

(2.7) можно найти, например, область на плоскости (b, Eотн ) , в которой возможно

классическое описание при заданной начальной энергии падающей частицы и конкретном виде потенциала взаимодействия. Малым углам рассеяния ϑ соответствуют, как правило, относительно большие прицельные расстояния, так что произведение ϑrm (b, Eотн ) может по-разному вести себя с ростом

прицельного параметра. Классическое описание при больших b несправедливо только тогда, очевидно, когда произведение ϑrm (b, Eотн ) с ростом b стремится к

нулю.

В то же время с ростом прицельного расстояния уголрассеяния,оставаясьмалым, убывает для реалистических потенциалов очень медленно, в результате чего произведение ϑrm (b, Eотн ) остается конечным и достаточно большим, что

обеспечивает квазикласичность рассеяния. Этот вывод можно переформулировать и в терминах орбитального момента движения l падающих частиц. При больших прицельных расстояниях для оценки величины орбитального момента можно воспользоваться приближенным равенством prm = µvrm ≈ µvb = kb = l. Тогда

условие (2.6) приобретает вид сильного неравенства

1 <<ϑl ,

из которого следует, что при больших значениях орбитального момента движение можно считать квазиклассическим.

2.2 Стационарнаятеориярассеяния

При рассмотрении процессов рассеяния в рамках квантовой механики дифференциальное сечение по-прежнему является той физической величиной, которую необходимо определить. Обобщение понятия дифференциального сечения рассеяния при рассмотрении методами квантовой механики легко получается, как отмечалось выше, с помощью соотношения (1.3), записанного в виде

σ(ϑ) = lim	Φr r2	,	(2.8)
r→∞	Φ

где r - расстояние до центра рассеяния, Φr - радиальная плотность потока

рассеянных частиц и Φ - плотность потока падающих частиц. В такой постановке задача сводится к вычислению сечений с помощью уравнения Шредингера путем

определения потоков частиц до и после рассеяния.

В нашем случае независящее от времени (стационарное) уравнение Шредингера в относительной системе отсчета следует записать для частиц с

приведенной массой µ , полной энергией Eотн = p2 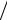2µ и импульсом p = kt . Тогда при заданном потенциале взаимодействия V (r ) с неподвижным центром рассеянияуравнение Шредингера имеет вид:

	2
−		∆ψ(r ) +V (r )ψ(r ) = E			ψ(r ) .	(2.9)
	2µ				отн

На бесконечности, где потенциал обращается в нуль, асимптотическое поведение волновой функции ψ(r ) , дающей полную информацию о состоянии частицы,

описывается выражением

	ik r		eikr
ψ(r ) = C{e t		+ f (ϑ,ϕ)	r }.

(2.10)

Оно имеет ясный физический смысл– бесконечно удаленными от центра рассеяния являются как падающие, так и рассеянные частицы, поэтому стационарное асимптотическое решение (2.10) представляет собой суперпозицию плоских падающих волн (первое слагаемое) и сферически расходящихся после рассеяния волн (второе слагаемое). При упругом рассеянии модули волновых векторов падающих и рассеянных волн совпадают и равны:

kt = ks = k = 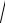2µEотн .

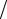Величина f (ϑ,ϕ) называется амплитудой рассеяния и для сферическисимметричных потенциаловV (r ) =V (r) не зависит от азимутального углаα .

Вектор плотности потока частицв квантовой механике дается выражением

	j(r ) = −i		(ψ ψ −ψ ψ ) .		(2.11)
		2µ

Интеграл от этого вектора по любой поверхности показывает вероятность того, что частица пересечет эту поверхность за единицу времени. Если подставить в выражение (2.11) первое слагаемое из (2.10), то получим величину плотности падающего потока:

j	t	= v		C		2 .	(2.12)

Легко заметить, что при выборе нормировочной константы в виде C = n выражение (2.12) в точности совпадет с классическим определением величины

полного потока: jt ≡ Φ = vn . С учетом такой нормировки второе слагаемое в

выражении (2.10) при подстановке в формулу (2.11) дает выражение для величины плотностирассеянного потока:

js = Φr = vn			f (ϑ,ϕ)		2	.	(2.13)
			r2

Заметим, что подстановка волновой функции в общее выражение (2.10)по частям при вычислении плотности потока не является, строго говоря, корректной. При этом не учитываются перекрестные произведения для падающих и рассеянных частиц или, иначе, не учитывается интерференция между падающей и рассеянной волнами. На практике, однако, падающий пучок частиц и рассеянные частицы можно в принципе отделить друг от друга с помощью соответствующих коллиматоров. Тогда указанные интерференционные явления будут существенными только для очень малых углов рассеяния (рассеяние вперед).

Как видим, отношение js 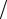jt равно отношению рассеянного и падающего

потоков частиц, поэтому из определения (2.8) после подстановки (2.12) и (2.13) получаем дифференциальное сечение рассеяния квантовой теории:

σ(ϑ,ϕ) =		f (ϑ,ϕ		2 .	(2.14)

Таким образом, решение задачи о вычислении амплитуды рассеяния для асимптоты волновой функции (2.10) дает полную информацию о дифференциальном сечении рассеяния. Асимптотическое поведение волновой функции действительно определяет дифференциальное сечение рассеяния, но его нельзя найти,не решив уравнение Шредингера (2.9) во всем пространстве.

2.3 Методпарциальных волн

Как известно, общего метода решения волновых уравнений, в том числе и уравнения Шредингера, не существует. Однако существенного упрощения можно добиться, если учесть, что для многих практически важных случаев потенциалы взаимодействия являются сферически-симметричными. Тогда переменные волновой функции в сферических координатах разделяются, что дает возможность найти некоторое общее выражение для амплитуды рассеяния в асимптотическом представлении (2.10) и соответствующее ему выражение для сечения рассеяния. На практике такой способ решения, который называют методом парциальных волн, особенно хорошо подходит для малых начальных энергий. В обратном предельном случае потенциал взаимодействия можно рассматривать как малое возмущение, что дает возможность воспользоваться результатами стационарной теории возмущений и так называемым борновским приближением теории рассеяния. Это приближение дополняет метод парциальных волн на случай больших по сравнению с энергией взаимодействия начальных энергий.

Если потенциал V (r) сферически-симметричен, то зависимость волновой

функции от угловых переменных сводится к зависимости только от угла ϑ , а общее решение уравнения Шредингера можно искать в виде

ψ(r ) =ψ(r,ϑ) = ∑R (r)P (cosϑ),			(2.15)
∞
l=0	l	l
где Pl (cosϑ) - полином Лежандра порядка		l . По физическому	смыслу

выражение (2.15) представляет собой сумму парциальных волн, различающихся орбитальным моментом движения l . При этом уравнение для радиальной функции Rl (r) имеет вид

∂2 (rR )	+[k 2 −	l(l +1)	− k 2	V (r)	](rR ) = 0 .	(2.16)
l
∂r2		r2		Eотн	l

Из уравнения (2.16) сразу вытекает, что при r → ∞ асимптотическое решение для рассеянных частиц действительно нужно выбирать в виде (2.10).

Точные решения уравнения (2.16) в отсутствие потенциала известны. Одно из них представляет собой так называемую сферическую функцию

	Бесселя jl (kr). Асимптотически на		больших расстояниях	сферическая
	функция Бесселя порядка l имеет вид стоячей волны
	jl (kr)	1	sin(kr −l π ) .	(2.17)
		kr
			2

Формально существует еще одно решение уравнения (2.16) – сферическая функция Неймана, асимптотика которой на больших расстояниях оказывается пропорциональной косинусу. Однако решение в виде функции Неймана не подходит из-за того, что оно расходится при r → 0 , а искомая волновая функция должна быть справедливой не только на больших расстояниях, но во всем пространстве, включая начало координат.

Отсюда следует, что с учетом решения (2.17) асимптотическое поведение волновой функции (2.15) описывается выражением

ψ(r,ϑ) = ∑R (r)P (cosϑ)

∑ al

sin(kr −l π +δ )P (cosϑ) ,

∞

∞

l

l

l

l

l=0

l=0 kr

2

которое можно представить в виде

ψ(r,ϑ) ∑

l

P (cosϑ){(−i)

e

iδ

l e

ikr

−i

e

−iδ

l e

−ikr

}.

(2.18)

∞

a

l

l

l=0

2ikr

l

Постоянные разложения al

следует

выбрать

так,

чтобы функция

ψ(r,ϑ)

асимптотически вела себя на больших расстояниях так же, как волновая функция (2.10). Фазовый сдвиг δl l -й парциальной волны представляет собой

разность фаз между асимптотическим решением уравнения (2.16) в присутствии потенциала и асимптотическим решением (2.17) в его отсутствие. Иными словами, влияние потенциала взаимодействия в методе парциальных волн сводится к появлению дополнительной фазы у каждой парциальной составляющей.

Теперь нужно лишь приравнять выражения (2.18) и (2.10), разложив предварительно выражение (2.10) по полиномам Лежандра:

ψ(r,ϑ) = C{exp(ikr cosϑ) + f (ϑ) exp(ikr)} = r

		C	∞	(2l +1)P (cosϑ)[(−1)l+1 e−ikr + eikr ] + C		∞
	=		∑			∑ f P (cosϑ)eikr ,		(2.19)
		2ikr l=0		l	r	l=0	l l

где коэффициенты разложения fl называются парциальными амплитудами рассеяния. Сравнив (2.19) с (2.18), получаем

	a		= C(2l +1)il exp(iδ		) ,	(2.20)
		l		l
	fl =		1	(2l +1)[exp(2iδl ) −1].		(2.21)
		2ik

В результате зависимость амплитуды рассеяния от фазовых сдвигов δl описывается выражением

f (ϑ) =	1 ∑(2l +1)(S			−1)P (cosϑ) ,	(2.22)
		∞
			l	l
	2ik l=0

а полная волновая функция приобретает вид

	ψ(r,ϑ)	1	∞	(2l +1)P (cosϑ){(−1)l+1 e−ikr + S		eikr }.	(2.23)
			∑
		2ikr l=0		l	l

Здесь введена величина

Sl = exp(2iδl ) ,

которая является диагональным матричным элементом так называемой

матрицы рассеяния.

Подставляя (2.22) в (2.14), приходим к следующему выражению для дифференциального сечения рассеяния

σ(ϑ) = k −2		∞	(2l +1)eiδl sin δ	P (cosϑ)		2
						.
		∑
		l=0	l	l

Если проинтегрировать это выражение по всем углам рассеяния, то получим полное сечение рассеяния. Тогда с учетом условия нормировки полиномов Лежандра

∫ Pl (cosϑ)Pm (cosϑ)sinϑdϑ = 2			δlm
π
0		2l +1
получаем	4π ∑(2l +1)sin2		δl ≡ ∑σl .	(2.24)
σ = 2π ∫σ(ϑ)sinϑdϑ =
π	∞		∞
0	k 2 l=0		l=0

Каждый из членов этой суммы представляет собой парциальное сечение для рассеяния частиц с заданным орбитальным моментом l . Выражение (2.24) в полной мере иллюстрирует волновой характер процесса рассеяния при квантовом описании. В частности, при больших значениях l , как отмечалось