3.РАССЕЯНИЕ ЧАСТИЦ НА АТОМАХ

3.1Столкновения электронов с атомами

Как отмечалось в разделе 1, в процессе торможения кинетическая энергия заряженных частиц может идти на возбуждение и ионизацию атомов среды, что является главным механизмом потерь энергии при прохождении любой заряженной частицы через вещество. Понятно, что ввиду равенства масс при взаимодействии первичного падающего электрона с электроном атомной оболочки передача энергии может быть особенно эффективной. Более подробно вопрос об ионизационном торможении и δ -электронах будет рассмотрен в связи ионизационными потерями при прохождении заряженных частиц. В этом разделе при рассмотрении облучения вещества высокоэнергетичными заряженными частицами, например электронами, главное внимание уделяется их взаимодействию с атомными ядрами (ядерное торможение). В общем случае это взаимодействие приводит, с одной стороны, к упругому и неупругому рассеянию на ядрах, а с другой стороны, при достаточно большой передаче энергии может стать непосредственной причиной структурных дефектов из-за вылета из молекул атомов отдачи.

Рассмотрение начнем с упругих столкновений с ядрами быстрых электронов. В пренебрежении экранированием ядер атомными электронами взаимодействие между электроном с зарядом −e и атомным ядром с зарядом

z2e описывается кулоновским потенциалом притяжения V (r) = − z2e2 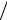r . Для

получения соответствующего классического (нерелятивистского) дифференциального сечения рассеяния необходимо установить зависимость угла рассеяния от параметров сталкивающихся частиц, в частности, от прицельного расстояния. Угол рассеяния в относительной системе отсчета, который дается формулой (П.24), определяется в этом случае табличным интегралом, вычисление которого приводит к общему выражению вида:

ϑ =π − 2b	∞ 1−	C1	− b2	−1 2	dr = 2arcsin	С1	2bEотн	,	(3.1)
	∫	Eотнr	r2		r2	[1+ (С1	2bEотн )2 ]1 2
	rm

где для рассматриваемой задачи C1 = −z2e2 < 0 , а расстояние максимального сближения определяется из уравнения

1−

C

−

b2

= 0

1

E

отн

r

r 2

и равно

m

m

C

C

2

1 2

rm = b

1

+ 1+ (

1

)

,

(3.2)

2bEотн

2bEотн

Непосредственно из выражения (3.1) получаем

sin

ϑ

=

С1

2bEотн

2

[1+ (С

2bE

отн

)2

]1 2

или

1

ϑ

C1

tg

=

.

(3.3)

2

2bEотн

Приведенные выражения справедливы при любом знаке постоянной C1

и, в частности, для таких отрицательных значений, при которых не происходит захвата частицы. В случае отталкивания, когда C1 > 0,

минимальное из расстояний максимального сближения R(Eотн ) получается, очевидно, из формулы (3.2) при подстановке b = 0 и равно R(Eотн ) = C1 Eотн = = C1 (m1 + m2 )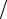E1m1 , в соответствии с чем для угла рассеяния имеем:

tg(ϑ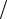2) = R(Eотн )2b.

Из определения дифференциального сечения рассеяния получаем

b

db

C

2

1

0 ≤ϑ ≤π

при C1

> 0

σР (ϑ) =

1

,

. (3.4)

=

4

при C1

< 0

sinϑ

dϑ

4Eотн

sin

(ϑ 2)

−π ≤ϑ ≤ 0

Сечение (3.4), которое представляет собой общее сечение Резерфорда, не зависит от знака C1 и угла ϑ , поэтому оно пригодно как для кулоновских

потенциалов отталкивания, так и для потенциалов притяжения. В рассматриваемом случае рассеяния электрона с массой m1 = me << m2 на ядре

величина Eотн = µv2 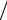2 ≈ mev2 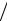2 = E1 , поэтому

	z2e		2		2	1			z2e	2		2	1			1	(z2e	2	)	2	1
														=								. (3.5)
σР (ϑ) =	4E					sin4 (ϑ	2)		2m v2				sin4 (ϑ 2)		16 E			2			sin4 (ϑ 2)
		отн							e						1

Дифференциальное сечение передачи энергии получается из выражения (3.5) по общей формуле:

σР (T; E1 ) =σ(ϑ) 4π

C1

2

4πTm π me

(z2e

)

2

1

.

(3.6)

=

2

T

4E

T 2

m E

T 2

m

отн

2

1

Здесь и далее используются общепринятые в ядерной физике обозначения T и

Tm вместо E2′ и E2′max . Из

выражения

(3.6)

следует,

что

существенно

преобладают, как показано на рис.3.1, малые значения передаваемой энергии, соответствующие рассеянию вперед. Такая особенность рассеяния связана с дальнодействующим характером кулоновских сил, из-за которого налетающие электроны практически всегда проходят через области действия слабых сил, передают относительно небольшую энергию и рассеиваются на малые углы.

При небольших углах рассеяния и малых передаваемых энергиях

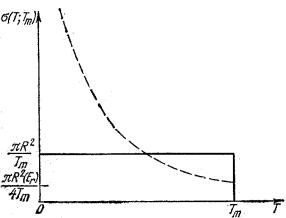
2

1

Рис.3.1 Дифференциальное сечение передачи энергии: 1 – потенциал жесткой сердцевины; 2 – кулоновский потенциал.

дифференциальные сечения (3.5) и (3.6) расходятся так сильно, что полное сечение, строго говоря, оказывается бесконечным. В действительности при столкновениях с атомными системами пользоваться простым потенциалом 1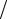r

не следует, его нужно видоизменить при больших r на какой-либо экранированный. Необходимо подчеркнуть, что при малых углах рассеяния такое поведение для потенциала 1r сохраняется и при квантовом описании,

которое приводит в точности к той же самой формуле (3.5), что и классическая теория. С помощью условия (2.6) квазиклассичности описания рассеяния несложно убедиться, что рассеяние потенциалом 1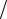r можно

рассматривать с помощью классической механики только для малых кинетических энергий, когда углы рассеяния оказываются достаточно большими.

Несмотря на расходимость дифференциальных сечений рассеяния (3.5) и (3.6), с их помощью можно оценить полное сечение процессов, сопровождающихся появлением атомов отдачи в результате упругого рассеяния высокоэнергетичных электронов на ядрах. В действительности быстрый электрон, как будет показано ниже, теряет на ионизацию, возбуждение атомов и некоторые другие процессы, типа тормозного излучения в поле ядра, практически всю свою энергию, которая в конечном счете превращается в тепло. Однако та малая доля энергетических потерь, которая идет на упругие столкновения с атомными ядрами, объясняет появление структурных дефектов во многих материалах. В Cu для электронов с энергией 3МэВ доля потерь энергии на образование структурных дефектов составляет всего 10-5.

Чтобы оценить полное сечение таких процессов, учтем, что существует некоторое пороговое значение Td переданной энергии, которое не может быть

меньше, чем энергия связи атома в молекуле или в кристаллической решетке.

Истинное среднее значение Td еще выше и включает в себя затраты энергии

на преодоление потенциального барьера (атома в решетке или в молекуле) и неупругие потери на возбуждение атомных электронных оболочек. В результате путем интегрирования выражения (3.6) получаем следующее парциальное сечение образования атомов отдачи:

me (z2e2 )2 Tm dT

me

(z2e2 )2

1

1

σ(Td ; E1 ) =π

∫

2 =π

−

,

(3.7)

m2

E1

m2

Td T

E1 Td

Tm

где Tm = 4me E1

m2 , а макроскопическое сечение получается умножением на

концентрацию

атомов мишени:

Σ2 (E1 ) = n2σ(Td ; E1 ).

Множитель

me m2 в

формуле (3.7) поясняет малость этого сечения даже при столкновениях с самыми легкими атомами водорода в молекулах воды. Для образования же структурных дефектов в конденсированных средах, связанных с отдачей атомов, необходимо также, чтобы электроны имели энергию E1 ≥0,2-0,5МэВ,

поскольку из-за малой массы они всегда характеризуются малой передачей энергии ядру. Такая высокая энергия, с одной стороны, дает электрону возможность проникнуть через электронные оболочки атома и, следовательно, оправдывает пренебрежение экранированием ядер. С другой стороны, это говорит о необходимости использовать релятивистское описание рассеяния, поскольку в этом случае кинетическая энергия электрона сравнима с его энергией покоя и β = v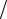1 c ≈1.

3.2 Релятивистское и квантовое сечения рассеяния электронов

Релятивистские сечения Дарвина-Резерфорда, соответствующие приведенным выше нерелятивистским резерфордовским сечениям, описываются при z2 <<137 простым выражением

2

z2e

2

2

1− β

2

σ ДР (ϑ) = (1− β

)σ

ДР (ϑ)

=

2m v

sin4 (ϑ 2)

=

2

e

1

z2

2

e

2

2

1− β

2

1

,

(3.8)

= 4

β4

sin4 (ϑ 2)

m c2

e

где e2 m c2

= 2,8 10−13

см – классический радиус электрона. Выражение (3.8)

e

получается при замене массы покоя электрона в (3.5) релятивистской массой

m (1− β 2 )1 2

. Аналогичным образом релятивистское сечение отдачи

e

4π

z2e

2

2

(1

− β

2

)Tm

σ ДР (T; E1 ) =σ(ϑ)

,

(3.9)

T

2m v

T 2

= 4π

2

m

e

1

в котором максимальная передаваемая энергия описывается формулой (П.56)

T	=αE	1	+ E	2m c2	≥αE ,	α = 4m m (m		+ m )	2	,
			1	e
				2m c2
m	1 1+α E				1	e 2	e	2
			1	e

и выражается через релятивистскую кинетическую энергию электрона в

лабораторной	системе	отсчета	E	= m c2[(1− β2 )−1 2	−1].	Кроме	выполнения
неравенства	me << m2		1	e
		будем	также полагать, что кинетическая энергия
электрона мала по сравнению с				энергией покоя	ядра	E << m		c2 . Тогда
максимальная передаваемая энергия принимает вид						1	2
		T	= 2 me m c2[(ε +1)2 −1],					(3.10)
		m		e
				m2

где ε = E1 mec2 и mec2 = 0,511МэВ – энергия покоя электрона. Понятно, что при E1 << mec2 выражение (3.10) и сечение рассеяния (3.9) сводятся к

соответствующим резерфордовским выражениям.

В действительности взаимодействие электрона с ядром является существенно квантовым, в чем легко убедиться, если получить условие применимости классической релятивистской механики. Как показано выше, классическое описание предполагает, что де-бройлевская длина волны электрона мала по сравнению с классическим расстоянием максимального

сближения r (0, E	отн	) = z	e2	E	отн	. Для релятивистского электрона де-
m		2

бройлевская длина волны должна определяться из соотношения (П.42), поэтому при v ≈ c получаем условие

	z α = z		e2	≈ z		1	>>1,	(3.11)
		2 c			2 137
	2

где α - постоянная тонкой структуры. Для реальных элементов это условие не выполняется, очевидно, никогда, поэтому корректным является только квантовое описание рассеяния быстрых электронов на ядрах.

Квантовое сечение рассеяния электрона на точечном ядре с определенным зарядом z2 вычислил Мотт с использованием релятивистской

квантовой теории Дирака для электронов (квантовая электродинамика). Аналитически получающиеся в результате бесконечные ряды для сечений были оценены Мак-Кинли и Фешбахом. Эти аналитические выражения удобно представить в виде отношения точного в заданном по z2α и β

приближении квантового сечения к релятивистскому сечению ДарвинаРезерфорда. В частности, при z2α <<1 с точностью до членов порядка β2 и z2αβ справедливо выражение

σМФ (ϑ)

=1

− β

2

sin

2

ϑ

+ z2αβπ sin

ϑ

−sin

ϑ

,

(3.12)

σ ДР (ϑ)

2

1

2

2

которое пригодно для

элементов

с z2 < 30 .

Если

подставить

в (3.12)