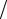
σtot =σe +σr = 2πR2 .

Отметим также, что частицы, образующиеся в результате прямых ядерных реакций, рассеиваются преимущественно вперед.

Интересно, что выражение для полного сечения упругого рассеяния можно получить и прямым вычислением с использованием асимптотического выражения для амплитуды рассеяния (2.29) либо ее представления (2.31). Задача в рассматриваемом случае полностью аналогична фраунгоферовской дифракции света на абсолютно черном шарике, характеризующейся малыми углами рассеяния. Соответствующая амплитуда дифракционного рассеяния нейтрона имеет вид

f (ϑ) = i	R J	(kRϑ) ,	(2.38)
	ϑ 1

и приводит к тому же результату (2.37) для полного упругого рассеяния. Заметим, что приведенный расчет можно обобщить и на случай быстрых тяжелых заряженных частиц, способных к сильному неупругому взаимодействию с ядрами. Для таких частиц при l ≤ kR можно по-прежнему полагать Sl = 0 , а при l > kR учесть упругое рассеяние в кулоновском поле,

для которого Sl = exp(2iδl ) .

2.6 Виды потенциалов взаимодействия

Для иллюстрации и ради последующих приложений приведем несколько примеров конкретных потенциалов взаимодействия, часть из которых можно рассмотреть точно по крайней мере в классической теории рассеяния. В частности, столкновение двух абсолютно жестких непроницаемых сфер с радиусами r1 и r2 часто хорошо подходит для описания взаимодействия

нейтральных частиц с атомами. Взаимодействие равно нулю на расстояниях r > r1 + r2 и резко возрастает, когда две сферы достигают расстояния r = r1 + r2 .

Для описания рассеяния в этом случае часто используют потенциал жесткой сердцевины (см. рис.2.2), который имеет вид:

∞	при r ≤ R = r1	+ r2	,	(2.39)
V (r) =	при r > R .
0

Легко видеть, что в потенциал (2.39) радиусы сталкивающихся частиц входят лишь в виде суммы, поэтому вместо двух сфер с тем же успехом можно рассматривать взаимодействие точечной массы, налетающей на непроницаемую сферическую мишень с радиусом R = r1 + r2 . Величину R

называют радиусом жесткой сердцевины.

Степенной потенциал вида

V (r) = C1 r

(2.40)

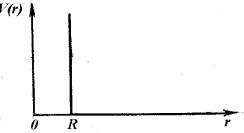
Рис.2.2 Потенциал жесткой сердцевины

хорошо известен по кулоновскому рассеянию. При кулоновском взаимодействии константа

C1 = (z1e)(z2e)

описывает взаимодействие двух точечных зарядов z1e и z2e , где e -единичный заряд и z1 , z2 - зарядовые числа. Потенциал (2.40) соответствует притяжению при C1 < 0 и отталкиванию при C1 > 0 .

Непосредственным обобщением потенциала (2.40) является степенной потенциал

V (r) = C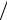rn ,

где C и n – варьируемые параметры. Этот потенциал, параметры рассеяния для которого табулированы, использовался, например, в работах по кинетике газов. В частности, степенной потенциал с n = 6 применяется для описания ван-дер-ваальсовых сил, которые заставляют атомы притягиваться друг к другу. Такие силы притяжения возникают из-за наличия взаимодействия между флуктуирующими электрическими диполями, образованными электронным облаком и положительно заряженным ядром каждого атома. Однако два атома могут сближаться лишь до тех пор, пока их электронные облака не начнут перекрываться. Дальнейшее сближение приводит к сильному взаимному отталкиванию, которое в конденсированных средах, включая твердые тела, часто описывают при помощи потенциала Ленарда-Джонса

V (r) = C2 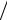r12 −C1 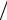r6 .

В результате конкуренции между притяжением и отталкиванием устанавливается некоторое оптимальное равновесное расстояние D , как показано на рис.2.3, что приводит к понятию эффективного радиуса атома.

Наибольшие проблемы возникают при рассмотрении упругих столкновений составных частиц, например межатомных столкновений или столкновений тяжелых заряженных частиц с атомами. Понятно, что описание потенциалов взаимодействия быстрого иона из падающего извне пучка или атома отдачи с большой энергией внутри образца с атомом вещества

Рис.2.3 Форма межатомного потенциала и положение равновесного расстояния D, равного для твердых тел величине порядка 2-3Å

представляет большой интерес при рассмотрении взаимодействия излучения с различными мишенями. Поэтому далее кратко остановимся для обсуждения вопроса, можно ли правильно описать взаимодействие двух сталкивающихся составных частиц с помощью того или иного потенциала и если можно, то в каком аналитическом виде следует выбирать такой потенциал взаимодействия.

При рассмотрении динамики столкновения необходимо корректно учесть прежде всего два наиболее важных фактора – зависимость характера столкновения от относительной скорости взаимодействующих составных частиц и возможность сопутствующих неупругих процессов, в частности, возбуждения атомных электронов и ионизацию. Если относительная скорость налетающей частицы невелика по сравнению со скоростями орбитальных электронов, то параметры столкновения определяются потенциалом взаимодействия фактически нейтральных атомов. Такое взаимодействие становится сильным только при непосредственном сближении ядер, а неупругие потери энергии, связанные с ионизацией и возбуждением атомов, незначительны по сравнению с кинетической энергией налетающего атома. Именно в этой ситуации рассеяние, сопровождающееся образованием структурных дефектов, вполне корректно считать упругим (атомы в основном состоянии) и описывать с помощью соответствующего короткодействующего потенциала.

Единой аналитической формулы для межатомного потенциала, пригодной для любых атомов и любых расстояний между ними, не существует. Существует, однако, эмпирическое правило, в соответствии с которым столкновения, приводящие к заметному рассеянию, определяются потенциалом на расстояниях порядка половины равновесного расстояния D между ближайшими соседями или меньших (для твердых тел r ≤1Å). На таких малых расстояниях можно пренебречь дальнодействующими межатомными силами притяжения, определяющими силы связи и сами

равновесные расстояния, как показано на рис.2.3. Это означает, что потенциал, описывающий процесс рассеяния, всегда является потенциалом чистого отталкивания и зависит в основном от электронов внутренних оболочек атомов. Отсюда вытекает, что потенциал взаимодействия зависит от расстояния максимального сближения, которое в свою очередь определяется кинетической энергией налетающей частицы. При значительных кинетических энергиях имеется глубокое взаимное проникновение электронных оболочек сталкивающихся атомов.

Заметим, что даже в тех случаях, когда рассеяние атомов можно рассматривать классически, потенциал их взаимодействия должен определяться с помощью квантового рассмотрения самих атомов. Наиболее простыми моделями, которые позволяют вычислить межатомный потенциал, являются квантовые статистические модели атома Томаса-Ферми и Томаса- Ферми-Дирака. В модели Томаса-Ферми атом представляет собой положительное ядро, окруженное непрерывно распределенными электронами. Эта модель является статистической потому, что распределение электронов получают с помощью квантовой статистики с учетом принципа запрета Паули, причем точность модели повышается с увеличением атомного номера. Модель атома Томаса-Ферми-Дирака учитывает эффекты обменного взаимодействия между электронами. В более сложных теориях принимают во внимание оболочечную структуру реальных атомов и используют суперпозицию электронных плотностей отдельных оболочек, определенных по методу Хартри-Фока.

Преимуществом потенциала взаимодействия в модели Томаса-Ферми, благодаря которому он широко используется при расчетах атомного рассеяния, является его универсальность при описании взаимодействия между любыми двумя атомами. Потенциал Томаса-Ферми между двумя атомами с зарядами ядер z1e и z2e записывают в виде

V (r) = z z		e2 ϕ(r aТΦ ) .	(2.41)
1	2	r

По существу это экранированный кулоновский потенциал с некоторой функцией экранирования Томаса-Ферми ϕ(r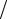aТΦ ) , где r - расстояние между

ядрами, а aТΦ - характерная длина экранирования, которую можно выразить через боровский радиус aH = 2 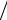mee2 = 0,53Å первой электронной орбиты в

атоме водорода. В частности, в качестве характерной длины экранирования выбирают, как правило, величины:

a	= (9π 2	128)1 3 a	H	(z 2 3	+ z 2 3 )−1 2	= (z 2 3	+ z 2 3 )−1 2	0,47 Å,	(2.42)
ТΦ				1	2	1	2
a	= (9π 2	128)1 3 a	H	(z 1 2	+ z 1 2 )−2 3	= (z 1 2	+ z 1 2 )−2 3	0,47 Å.
ТΦ				1	2	1	2

При большой относительной скорости налетающая составная частица становится точечным зарядом z1e, взаимодействие которого только с

электронами атомов вещества имеет кулоновский характер и описывается степенным потенциалом вида (2.40). Взаимодействие же такой частицы, например, протона, дейтрона или α -частицы, с ядром можно приближенно описать потенциалом Томаса-Ферми для отдельного атома-мишени, в результате чего длина экранирования зависит только от z2 :

aΦ = (9π 2 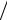128)13 aH z2 −13 = z2 −13 0,47 Å.

Функция экранирования Томаса-Ферми ϕ(x) табулирована и в зависимости от

задачи используются ее различные приближенные аналитические выражения. Для них известны численные значения таких параметров рассеяния, как угол рассеяния, расстояние максимального сближения, передача энергии и даже дифференциальные сечения рассеяния.

Ни при каких расстояниях между сталкивающимися атомами статистическая теория Томаса-Ферми неприменима в случае малых зарядовых чисел z , поэтому в интересующем нас диапазоне расстояний между ядрами потенциал Томаса-Ферми более других подходит для описания взаимодействия между достаточно тяжелыми ядрами. Это обстоятельство подтверждается экспериментально. Если отвлечься от статистических теорий атома, то для построения межатомных потенциалов, описывающих процессы рассеяния, можно использовать различные эмпирические и полуэмпирические функции и физические соображения. Понятно, например, что кулоновское взаимодействие заряженных ядер наиболее сильно видоизменяется из-за экранирования атомными электронами на больших расстояниях, поэтому для очень малых расстояний между ядрами Бор предложил кулоновский потенциал с экспоненциальным экранированием:

V (r) = z z					e2	exp(−r aБ ) .	(2.43)
			1	2		r
Параметром экранирования в потенциале Бора служит величина
a	Б	= a	H	(z 2		3 + z 2 3 )−1 2 ,	(2.44)
					1	2

а сама экспоненциальная функция в формуле (2.43) представляет собой грубое приближение к функции экранирования Томаса-Ферми ϕ(r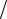aΦ ) .

Чисто экспоненциальное экранирование приводит к более быстрому убыванию потенциала (2.43) с ростом r по сравнению с потенциалом ТомасаФерми (2.41). Именно из-за слишком быстрого убывания с увеличением расстояния потенциал (2.43) неудовлетворительно описывает взаимодействие для больших расстояний между ядрами, например, больших 1Å в твердых телах, когда становятся существенными внешние электронные оболочки. Поэтому для описания взаимодействия часто используют, например, чисто экспоненциальный потенциал Борна-Майера:

V (r) =V0 exp(−r aБМ ) ,

(2.45)

который хорошо описывает отталкивание ионов с замкнутыми оболочками. Потенциал (2.45) используется также для приближенного

аналитического описания сложного межатомного потенциала, получающегося в модели Томаса-Ферми-Дирака. Кроме того, с его помощью можно построить иные достаточно интересные потенциалы. Например, известна следующая интерполяционная формула, которая при малых r сводится к кулоновскому потенциалу, а при больших – к потенциалу Борна-Майера:

V (r) =	z z	e2	exp(−r a	БМ	)	,	(2.46)
	1 2
	a
			1−exp(−r a)

где aБМ и a – подгоночные параметры. В то же время одна весьма

существенная черта, характерная для атомов, отсутствует у всех приведенных потенциалов, которые можно записать более или менее точно в аналитическом виде. Эти потенциалы не отражают оболочечную структуру атомов, которая приводит к выраженной немонотонной зависимости взаимодействия от зарядовых чисел z . А такая зависимость, как показывают эксперименты, существует.

Как было показано, за исключением очень малых расстояний, где неэкранированный и экранированные потенциалы совпадают, все потенциалы дают разную зависимость на различных расстояниях. В частности, потенциал Борна-Майера непригоден для малых расстояний, поскольку неспособен описать сильное кулоновское взаимодействие, тогда как кулоновский потенциал слишком велик на больших расстояниях, когда взаимодействие экранировано, что отражает по существу большой вклад в общее взаимодействие отталкивания электронных оболочек. Здесь преимущества имеет потенциал Борна-Майера. Следовательно, выбор потенциала взаимодействия в большой мере зависит от расстояния максимального сближения между атомами, которое в свою очередь зависит от заданной кинетической энергии.

Отметим, что силами чистого отталкивания хорошо описываются столкновения со значительной кинетической энергией. Однако окончательная судьба сталкивающихся частиц в конденсированных средах определяется в конце концов и силами, содержащими также компоненты притяжения, поскольку эти силы ответственны за силы связи. Это утверждение относится не только к твердым тел ам, но и к биологическим объектам, и имеет определенное значение для них при определении структуры радиационных дефектов и их устойчивости.

Задачи

Задача 2.1. Найти условие квазиклассического описания рассеяния в лабораторной системе, если известно, чтопри ϑ <1 выполняется условие (2.6)

квазиклассического описания в относительной системе отсчета. Решение. Условие (2.6) можно записать в виде

sin					<< sinϑ <1.	(2.47)
	pr	(b, E	отн	)
	m

Понятно, что при ϑ <1 выполнение этого сильного неравенства возможно

только тогда, когда аргумент синуса в левой части также много меньше единицы. Поэтому синус можно заменить его аргументом и переписать выражение (2.47) в виде

			<< p sinϑ .	(2.48)
r (b, E	отн	)
m

Расстояние максимального сближения не зависит, очевидно, от системы отсчета, поэтому искомое условие для лабораторной системы отсчета можно получить из неравенства (2.48) при помощи выражения (П.37) для угла рассеяния и определения импульса частицы с приведенной массой µ . Тогда

находим

m1m2

m1

p sinϑ < µvsinϑ = m

+ m

v1tgϑ1 m

+ cosϑ =

1

2

2

m1 + m2 cosϑ

< p1tgϑ1 .

(2.49)

= p1tgϑ1

m

+ m

1

2

Следовательно, выполняется сильное неравенство

<< tgϑ1 .

(2.50)

p1rm (b, Eотн )

Теперь учтем, что при любом отношении масс сталкивающихся частиц уголϑ1

всегда меньше углаϑ , поэтому из условия

ϑ1

<

ϑ

<1 вытекает,

что величина tgϑ1

по порядку величины равна единице. Но отсюда сразу следует, что в левой части неравенства должна фигурировать величина много меньше единицы, которую можно заменить ее тангенсом. В результате получаем сильное неравенство

tg p1rm (b, Eотн ) << tgϑ1 ,

непосредственно из которого при ϑ1 <1 вытекает искомое условие квазиклассического описания рассеяния в лабораторной системе отсчета

p1rm (b, Eотн ) <<ϑ1 ,

повнешнемувидувточностиповторяющееусловие(2.6).

Задача 2.2. Получить выражение (2.12) плотности потока частиц в падающей плоской волне.

Решение. Непосредственно из выражения (2.12) следует, что для решения задачи достаточно вычислить только мнимую часть одного из слагаемых в выражении (2.11):

	j(r ) =		Im(ψ ψ) .	(2.51)
		µ

Теперь находим i -ю компоненту градиента волновой функции плоской волны

C

∂

exp(ik

x

) = iCk

exp(ik

x )

∂xj

=

∂x

∂x

i

t j

j

t j

t l l

i

= iCk

t j

δ

ij

exp(ik

t l

x ) = iCk

t i

exp(ik

x ) → iCk

t

exp(ik

r ),

(2.52)

l

t l l

t

где δij - символ Кронекера, а по дважды повторяющемуся индексу как всегда подразумевается суммирование от 1 до 3. В результате находим

jt (r ) =		C		2	kt	= n	p	= nv .
				µ		µ

Задача 2.3. Получить выражение (2.13) плотности потока частиц в рассеянной сферически расходящейся волне.

Решение. Аналогично (2.52) находим

∂

1

− 2xjδij

1

2x

δ

exp(ik

x

2

) =

exp(ik

x

2

) +

ik

il

exp(ik

x

2

) =

l

l

l

m

∂xi

2(xk 2 )3 2

xj 2

xj 2

2

xk 2

ikr −1 r

ik

xj

2

−1 x

=

exp(ik

x

2

)

→

exp(ikr) .

i

xm

2

xk

2

l

r2

r

Подставляя это выражение в (2.51), получаем

2

f (ϑ,ϕ

r

ks

f (ϑ,ϕ

′

f (ϑ,ϕ

js (r ) =

C

(k

) = n

= nv

.

µ r2

r

µ

r2

r2

Отсюдасучетомравенства v′ = v вытекаетвыражение(2.13).

Задача 2.4. Доказать справедливость выражения (2.21) для парциальной амплитуды рассеяния.

Решение. Приравнивая выражения (2.18) и (2.19), можно получить функциональное равенство для рядов, представляющих собой разложения по полиномам Лежандра. Ввиду ортогональности полиномов, для выполнения равенства рядов необходимо равенство коэффициентов разложения, поэтому

al [(−i)l eiδl eikr −il e−iδl e−ikr ] = C(2l +1)[(−1)l+1 e−ikr + eikr ] + 2ikCfl eikr .

(2.52)

То же замечание об ортогональности относится и к экспоненциальным функциям в равенстве (2.52), имеющим разный знак показателя. Следовательно, можно требовать также равенства коэффициентов при каждой из экспонент по отдельности, что приводит к системе двух уравнений с двумя неизвестными al и fl :

		a (−i)l eiδl	= C(2l +1) + 2ikCf			l	,
		l
		− alil e−iδl	= C(2l +1)(−1)l+1 .
Второе из этих уравнений сразу дает выражение для коэффициентов
разложения al
	al	= −C(2l +1)(−1)i2li−l eiδl = C(2l +1)il eiδl .
Подстановка величины al в первое из ур				авнений системы позволяет
определить парциальную амплитуду рассеяния:
fl =	1	(2l +1)[il eiδl (−i)l eiδl −1] =		1	(2l +1)(e2iδl −1).
	2ik
				2ik

Задача 2.5. Получить выражение (2.24) для полного сечения рассеяния в методе парциальных волн.

Решение. Из выражения (2.23) с учетом условия нормировки полиномов Лежандра получаем

σ(k) = 2πk −2

∞

π

(cosϑ)Pm

(cosϑ)sinϑdϑ =

∑(2l

+1)(2m +1)ei(δl −δm ) sinδl sinδm

∫ Pl

m,l=0

0

∞

2

= 2πk −2

∑(2l +1)(2m +1)ei(δl −δm ) sinδ

sinδ

δ

=

l

m 2l +1

lm

m,l=0

∞

= 4πk −2 ∑(2l +1)sin2 δl

l=0

Задача 2.6. В борновском приближении получить выражение для амплитуды рассеяния на сферически-симметричном потенциале.

Решение. Формулу (2.28) можно записать в виде, где явным образом показаны интегралы по угловым переменным в сферической системе координат с осью z , направленной вдоль вектора рассеяния q :

f (ϑ) = −	µ	∞ π 2π	′	′	′	′	′ ′ ′2	′	.
	2π 2	∫∫ ∫V (r )exp{−iqr			cosθ }dϕ		sinθ dθ r	dr
		0 0 0

Тогда после интегрирования по азимутальному углу получаем

f (ϑ) =

µ

∞ π

′

′

′

′

′2

dr

′

.

(2.53)

2

∫∫V (r )exp{−iqr

cosθ }d(cosθ )r

0 0

После интегрирования в выражении (2.53) по полярному углу θ′ остающийся

интеграл по радиальной координате приобретает вид:

µ

∞

′

exp(iqr′) −exp(−iqr′)

′2

′

2µ ∞

′

f (ϑ) =

∫V (r )

r

dr

= −

∫V (r )

2

−iqr′

2

0

0

sin(qr′) r′2dr′. qr′