выше, движение можно считать квазиклассическим. Тогда путем подстановки классического выражения для орбитального момента l = bp в классическую

формулу для числа падающих частиц (1.2) находим парциальное сечение числа частиц в пучке, обладающих орбитальным моментом в интервале значений ∆l = k∆b :

σ(∆l) = ∫2πbdb 2π		l	∆l = π		2l∆l = π ∑2l .
b+∆b	2
b	p2			k 2		k 2	∆l

Сравнивая полученное выражение с формулой (2.24), можно прийти к выводу, что число частиц, рассеянных с моментом l , может оказаться в 4 раза большим числа таких частиц в падающем потоке. Это обстоятельство является чисто квантовым эффектом, связанным с интерференцией рассеянных волн.

Исследуя δl для больших значений l , можно показать также, что точное полное сечение рассеяния (2.24) остается конечным, если рассеивающий потенциал убывает при больших r быстрее, чем 1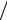r2 . Вычисление фазовых сдвигов δl в случае произвольных потенциалов представляет собой очень

трудную задачу, поэтому может показаться, что представление (2.24) для σ(ϑ) практически бесполезно. Фазовые сдвиги, однако, можно вычислить для

заданного потенциала численным интегрированием уравнения Шредингера и с помощью различных приближенных методов. Кроме того, найти полное сечение рассеяния (2.24) тем легче, очевидно, чем меньше слагаемых дают существенный вклад в сумму. Утверждение о существовании некоторого максимального орбитального момента рассеяния, ограничивающего суммирование в (2.24), аналогично утверждению о том, что частица испытывает существенное рассеяние только при b < rc . В частности, если

потенциал V (r) обращается в нуль за пределами расстояния rc , то

существенный вклад в сумму (2.24) вносят, очевидно, лишь слагаемые, соответствующие интервалу от l = 0 до l = kb < krc . Следовательно, чем

меньше величина krc , тем легче применять метод парциальных волн, так что

наиболее полезным он оказывается именно при малых энергиях. При учете лишь одного члена с l = 0 дифференциальное сечение рассеяния не зависит от угла рассеяния, в результате чего рассеянная волна обладает сферической симметрией. Это так называемое s -рассеяние или изотропное рассеяние.

2.4 Борновское приближение

Как отмечалось выше, если энергия налетающей частицы Eотн достаточно велика, то потенциал V (r) в уравнении Шредингера (2.9) можно

рассматривать как некоторое малое возмущение. В этом случае уравнение Шредингера решают методом последовательных приближений, разлагая искомую волновую функцию ψ(r ) в ряд по степеням потенциала. Для

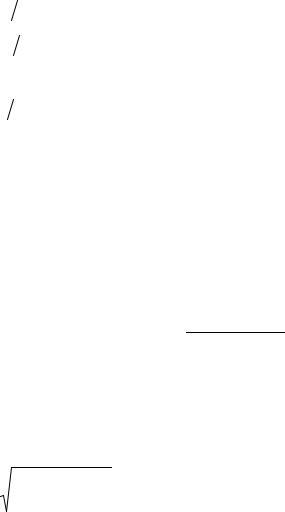
наглядности малого параметра разложения удобно ввести его в явном виде, заменяя в уравнении Шредингера потенциал V (r) на произведение λV (r) и

считая малым параметром именно величину λ . Тогда приближения различного порядка по возмущению будут определяться коэффициентами при соответствующих степенях λ . В окончательном же ответе достаточно положить λ равным единице.

Всоответствии с изложенным выше волновую функцию можно записать

ввиде разложения

ψ(r ) =ψ (0) (r ) + λψ (1) (r ) + λ2ψ (2) (r ) +....	(2.25)
Подставляя разложение (2.25) в уравнение (2.9) с потенциалом	λV (r) и

приравнивая величины при одинаковых степенях λ , получаем бесконечную систему зацепляющихся уравнений:

[( 2	2µ)∆ + Eотн ]ψ (0)	= 0,
[( 2	2µ)∆ + Eотн ]ψ (1)	=V (r )ψ (0) ,	(2.26)
………..…..….........		= …. …...,
[( 2	2µ)∆ + Eотн ]ψ (n)	=V (r )ψ (n−1) ,

Решение нулевого приближения, для которого возмущение в виде потенциала взаимодействия отсутствует, должно описывать, очевидно, падающую плоскую волну, поэтому

ψ =ψ (0) = C exp(ikt r ).

Это решение необходимо подставить в правую часть второго уравнения системы (2.26). Используя известную функцию Грина для волновых уравнений, получаем

(0)

(1)

µ

′

exp(ik

r − r′

)

ikt r′

′

ψ ≈ψ

+ψ

= C{exp(ikt r ) −

2π 2

∫V (r )

e

dr }, (2.27)

r

− r′

где член ψ (1) называют первым борновским приближением.

Асимптотическое поведение волновой функции (2.27) на больших расстояниях r >> r′ получается, если представить показатель подынтегральной экспоненты в виде

ik

= ikr

1

− 2

rr′

+

r′2

−

rr′

′,

r

− r′

r2

r2

ikr 1

r2

= ikr −iks r

где ks = k r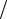r - волновой вектор рассеянной волны. Подставляя это выражение в формулу (2.27), находим

	µ	eikr	′	i(kt −ks )r′	′
ψ ≈ C{exp(ikt r ) −		r	∫V (r )e		dr }.	(2.28)
	2π 2

Сравнение асимптотической формулы (2.28) с аналогичным асимптотическим выражением (2.10) показывает, что в первом борновском приближении амплитуда рассеяния равна

	µ		′	−iqr′		′
f (ϑ) = −			∫V (r )e		dr		,	(2.29)
	2π 2
где q = ks − kt - изменение импульса			частицы				или	вектор рассеяния,

абсолютная величина которого равна q = 2k sin(ϑ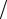2).

Далее, несложно получить выражение для амплитуды рассеяния на сферически-симметричном потенциале. После интегрирования по угловым переменным в (2.28) получаем

	2µ	′	sin qr′		′2	′
f (ϑ) = −		∫V (r )		r		dr	.	(2.30)
	2		qr′

Отметим, что выражения типа (2.29) и (2.30) обладают очень широким спектром применений в физике и используются, например, при описании рассеяния света и дифракционного рассеяния рентгеновского излучения (дифракционная томография), лежат в основе рентгеноструктурного анализа твердых тел, биологических макромолекул в кристаллической форме и т.д.

Можно установить прямую связь введенной ранее амплитуды рассеяния (2.22) с амплитудой рассеяния (2.29) в борновском приближении и получить таким образом зависимость диагонального матричного элемента матрицы рассеяния от потенциала взаимодействия, как функции прицельного расстояния b = r , где r - составляющая радиус-вектора частицы,

перпендикулярная к направлению x ее движения в падающем пучке волн. Для этого нужно учесть, что при больших значениях энергии наибольший вклад в сумму (2.22) вносят большие значения орбитального момента и малые углы рассеяния. Первое дает возможность перейти от суммирования по l к интегрированию, а второе позволяет представить в интегральном виде полиномы Лежандра. Тогда при непосредственном сравнении получающегося интегрального выражения с интегральным представлением (2.29) находим

	ik			−iqb
f (ϑ) =		∫[1	− S(b)]e		db ,	(2.31)
	2π

S(b) =1− iµ2k ∞∫V (b, x)dx .

−∞

В заключение отметим, что из решения системы уравнений (2.26) могут быть получены и более высокие приближения, что позволяет представить в виде ряда амплитуду рассеяния и диагональный матричный элемент матрицы рассеяния. Особое значение при этом имеет вопрос о сходимости ряда БорнаНеймана (2.25) и точности борновского приближения, поскольку вычислять следующие члены рядов становится все труднее.

2.5 Квантовое описание неупругого рассеяния

До сих пор при описании рассеяния предполагалось, что его можно рассматривать как результат процесса столкновения частиц друг с другом независимо от их реальной внутренней структуры и природы. Понятно, что такое описание справедливо только при определенных условиях и для определенного круга физических ситуаций. Однако общие методы квантовой теории позволяют исследовать рассеяние частиц и в тех случаях, когда начинают играть существенную роль процессы, приводящие, например, к изменениям внутреннего состояния сталкивающихся частиц и к неупругим потерям энергии, сопровождающим такие изменения. В общем случае под неупругими каналами реакции понимают самые разные процессы, включая процессы с изменением самого типа частиц. Характерным примером такого рода являются, например, прямые ядерные реакции, при которых падающая частица взаимодействует не с ядром, как целым, а с одним или несколькими нуклонами из приповерхностной области ядра. Для тяжелых падающих частиц прямые ядерные реакции начинают превалировать при энергии больше нескольких МэВ, что приводит к расщеплению легких ядер атомов мишени, реакции передачи нуклонов и другим процессам без образования промежуточного составного ядра.

Из формулы (2.22) видно, что полному отсутствию рассеяния (упругого и неупругого) с орбитальным моментом l соответствует равенство Sl =1. В

этом случае в полную волновую функцию (2.23) дают вклад только частицы с моментом l из падающего пучка волн. Из вида полной волновой функции также следует, что обратный предельный случай Sl = 0 соответствует полному

поглощению частиц в том смысле, что вообще отсутствует парциальная расходящаяся волна с моментом l , которая была в падающем пучке. Интересно, что в предельном случае полного поглощения только половина числа частиц с моментом l участвует собственно в неупругих процессах по всем возможным каналам. Вторая половина при этом обязательно претерпевает упругое рассеяние.

Действительно, уменьшение интенсивности парциальной расходящейся

волны, которая описывается величиной		Sl		2 , связано с неупругими

процессами, поэтому полное сечение неупругих процессов дается выражением

	σr =	π	∞	(2l +1)(1−		Sl		2 ) .	(2.32)
			∑
		k 2
			l=0

При этом выражение (2.24) по-прежнему описывает полное сечение упругого рассеяния

	σe =	π	∞	(2l +1)		1− Sl		2 ,	(2.33)
			∑
		k 2
			l=0

так что полное сечение рассеяния дается выражением

σtot =σe +σr =	2π ∑(2l +1)(1− Re Sl ) .
	∞
	k 2 l=0

Из выражений (2.32) и (2.33) сразу следует, что при Sl = 0 всегда выполняется

равенство σe =σr .

Выше отмечалось, что применение метода парциальных волн для практических оценок наиболее эффективно при малых относительных энергиях. Можно показать, что в этом случае

δl k 2l+1 .

Сучетом этого соотношения при k → 0 наибольший вклад вносит, очевидно, изотропное s-рассеяние с l = 0 , для которого получаем

S0 = exp(2iδ0 ) 1− 2iδ0 =1− 2ika =1+ 2ka2 − 2ika1 ,	(2.34)
где a - длина рассеяния, комплексная часть которой a2 ≤ 0	описывает

процессы неупругого рассеяния. Подстановка формулы (2.34) в (2.32) и (2.33) приводит к полным сечениям для упругого и неупругого рассеяния

σe = 4π					a		2 ,			(2.35)
σr =	4π				a2				,	(2.36)
	k

первое из которых не зависит от энергии, а второе описывает известный закон 1v для неупругих процессов.

Величину длины рассеяния a и ее мнимой части можно оценить для каждого конкретного механизма взаимодействия отдельно. В частности, если речь идет об упоминавшихся выше прямых ядерных реакциях, инициируемых,

например, нейтронами, то оказывается, что модуль длины рассеяния a = R , где R - радиус ядра, а величина a2 пропорциональна ширине d области

размытия ядерной поверхности. Такой результат сильно отличается от выражений, которые получаются в частном случае рассеяния на тяжелом ядре

срадиусом R быстрых нейтронов: kR >>1. Ввиду большой энергии нейтрона

иограниченного радиуса действия ядерных сил здесь обычно полагают, что нейтроны полностью поглощаются тяжелыми ядрами только при прямом попадании. Иными словами, нейтрон испытывает полностью неупругое рассеяние при b ≤ rc = R и l ≤ kR , поэтому для таких значений орбитального

момента имеем Sl = 0 .	Наоборот,			при l > kR	рассеяния нет вовсе:					Sl =1. В
соответствии с этим непосредственно из (2.32) и (2.33) находим										(2.37)
σr =σe	= π ∑(2l +1) 2π ∑l =				2π	k	2	R	=πR2 ,
			kR	kR
		k 2	l=0	k 2 l=0	k 2		2