1.4. Дискретизация сигналов. Теорема отсчетов. Сигналы с ограниченными и полосовыми спектрами

С целью упрощения задач анализа сигналов в инженерных расчетах учитывают только ту часть спектра, в которой сосредоточено до 80…95 % энергии сигнала. Поэтому чаще всего большинство сигналов рассматривают как сигналы с ограниченными спектрами. Для их анализа наряду с разложением Фурье широко применяют разложение Котельникова.

Рассмотрим основные особенности этого разложения.

Ортогональное разложение Котельникова для непрерывных сигналов с ограниченными спектрами позволяет представлять их в виде импульсных последовательностей. Теоретической основой разложения служит теорема Котельникова (теорема отсчетов): любая непрерывная функция S(t), не содержащая частот выше F, полностью определяется последовательностью значений в моменты, отстоящие друг от друга на время Dt=1/2F.

Общее число отсчетов n для сигнала длительностью Т будет равно n=T/Dt=2FT=n. Число n называют базой сигнала.

Для сигнала S(t), спектр которого лежит в интервале [0,F], ортогональное разложение Котельникова имеет вид

где S(kDt)=S_k – отсчет сигнала в момент времени t_k ;

[sin2pF(t-kDt)]/[2pF(t-kDt)] – базисная система ортогональных функций с общей нормой ½F; Dt=1/2F-интервал дискретизации, равный норме базисных функций. Функции g_k=[sin2pF(t-kDt)]/[2pF(t-kDt)] называют функциями отсчетов, а значения S(kDt) – отсчетами. График функции отсчетов имеет вид, представленный на рисунке ниже.

Ортогональность функций отсчетов проверяют путем вычисления интеграла

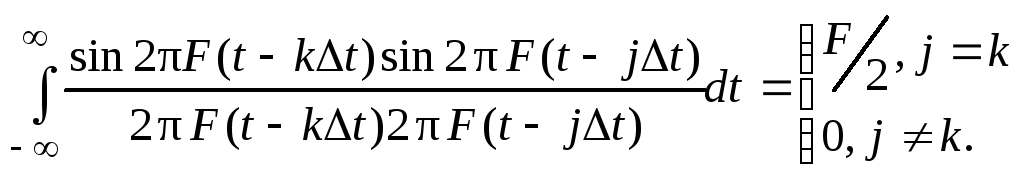
Интервал дискретизации не превышает половины периода наиболее высокой частоты спектра сигнала, что уменьшает число членов в данном разложении по сравнению с разложением Фурье при одинаковой точности аппроксимации. Точность аппроксимации так же, как и в случае разложения Фурье, определяется количеством учитываемых отсчетов. При этом мощность сигнала через заданную последовательность временных выборок выражается равенством Парсеваля:

- энергия сигнала

Е=;

-мощность сигнала за период колебания

P=.

Из последнего выражения следует, что средняя за период Т мощность непрерывного сигнала равна среднему квадрату выборки. Усреднение производится по всем интервалам, число которых 2FT.

Достоинства ортогонального разложения следующие: базисная система ортогональных функций выбрана так, что ряд Котельникова носит формальный характер, т. е. в любой момент отсчета t_k он дает одно значение S_k, остальные составляющие ряда вырождаются в нуль; коэффициенты ряда Котельникова можно не вычислять; их определяют путем измерения значений сигнала или из его аналитической формы; зная длительность сигнала Т и граничную частоту F, определяют требуемое число отсчетов n=2FT и энергию сигнала; относительная простота реализации как разложения (т. е. дискретизации) непрерывного сигнала в импульсную последовательность, так и последующего его восстановления.

Остановимся более подробно на последней особенности. Для этого рассмотрим физический смысл разложения Котельникова. Каждый член ряда представляет собой отклик идеального фильтра нижних частот g_k с частотой среза F на очень короткий импульс, приходящий в момент t_k=kDt и имеющий площадь S(kDt). Поэтому при дискретной передаче сигнала S(t) с ограниченным спектром необходимо через равные интервалы времени Dt брать отсчеты мгновенных значений сигнала и передавать по каналу последовательность достаточно коротких импульсов длительностью t, причем t/Dt<<1. Амплитуду импульсов A_k в момент времени t_k=kDt выбирают так, чтобы A_kt=S(kDt)=S_k. В приемном устройстве выделенная последовательность видеоимпульсов пропускается через фильтр нижних частот, на выходе которого восстанавливается переданный непрерывный сигнал. Длительность импульсов t может быть сколь угодно малой, но выбирают ее исходя из полосы прозрачности канала связи. Частота дискретизации ( тактовая частота ) равна 2F.