Бакалов В.П. Основы теории цепей_2007

ò. å. åäиничнàя импульснàя функция рàâ-

R

íà произâîäíîé åäиничной функции. Тàê

u1 =U

C

uC =u2

êàê ðàññìàòðèâàåìàÿ öåïü ïðåäïîëàãàåòñÿ

линейной, то соотношение (8.1) сохрàíÿ-

åòñÿ è äля импульсных

и перехоäíûõ

Ðèñ. 8.1

ðåàêöèé öåïè

h (t ) =

dg ( t )

= g¢(t ),

(8.2)

dt

т. е. импульснàÿ õàðàктеристикà ÿâляется произâîäной от перехоä- íîé õàðàктеристики цепи.

Óðàâнение (8.2) спрàâåäëèâî äëÿ ñëó÷àÿ, êîãäà g(0) = 0 (íóëå- âûå íà÷àльные услоâèÿ äëÿ öåïè). Åñëè æå g(0) ¹ 0, òî ïðåäñòàâèâ

g(t) â âèäå g(t) = g1 ( t ) + g ( 0 )1(t ) , ãäå g1 ( 0 ) = 0, получим урàâ- нение сâÿçè äëÿ ýòîãî ñëó÷àÿ:

h (t ) = g′ (t ) = g1′ (t ) + g ( 0 ) d (t ).

(8.3)

Äëÿ íàõîæäения перехоäных и импульсных хàðàктеристик цепи можно использоâàòü êàê êëàссический, тàê è îïåðàторный метоäы. Сущность клàссическоãî ìåòîäà состоит â îïðåäелении âременной реàêöèè öåïè (â форме нàпряжения или токà â îòäельных âåòâÿõ öåïè) íà âîçäåéñòâèå åäиничной 1(t) или импульсной d(t) функции. Обычно клàссическим метоäîì óäîáíî îïðåäелять перехоäíóþ õàðàктеристику g(t), à импульсную хàðàктеристику h(t) íàõîäить с помощью урàâнений сâÿçè (8.2), (8.3) èëè îïåðàторным метоäîì.

Пример. Íàéäåì êëàссическим метоäом перехоäíóþ õàðàктеристику по нàпряжению äля цепи, изобрàженной нà рис. 8.1. Численно gu(t) äëÿ äàííîé öåïè ñîâïàäàåò ñ íàпряжением нà емкости при поäключении ее â момент t = 0 к источнику нàпряжения U1 = l Â:

gu ( t ) = uC ( t ) U1=1( t ) .

Çàкон изменения нàпряжения uC(t) îïðåäеляется урàâнением (6.27), ãäе необхоäимо положить U = l Â:

gu ( t ) = 1 − e−tτ.

Ïðè íàõîæäåíèè õàðàктеристик g(t) è h(t) îïåðàторным мето- äом пользуются изобрàжениями функций 1(t), d(t) è ìåòîäèêîé ðàñ÷åòà перехоäных процессоâ, изложенных â ãë. 7.

Пример. Îïðåäåëèì îïåðàторным метоäом перехоäíóþ õàðàктеристику gu(t) RÑ-öåïè (ñì. ðèñ. 8.1). Äëÿ äàííîé öåïè â ñîîòâåòñòâèè ñ çàконом Омà â îïåðàторной форме (7.35) можем зàïèñàòü:

gu ( t ) UC ( p ) U1( p )=1p = I ( p ) pC1 ,

201

ãäå

I ( p ) =	U1 ( p )	=		1	=		C		(8.4)
								.
	Z ( p )		p ( R + 1 pC )				RCp + 1
Окончàтельно получàåì
	UC ( p ) =			1		.
				p ( RCp + 1)

Îòñþäà по теореме рàзложения (7.31) нàõîäèì

UC ( p ) gu ( t ) = 1 − e−1τ,

ò. å. òî æå çíàчение, что и полученное клàссическим метоäîì.

Ñëåäует отметить, что âеличинà I(ð) â óðàâнении (8.4) численно рàâíà изобрàжению перехоäíîé ïðîâîäимости. Анàëîãичное изобрàжение импульсной хàðàктеристики численно рàâíî îïåðàторной проâîäимости цепи

hY (t ) I ( p )

U1 ( p )=1

=

1

= Y ( p ).

Z( p )

Íàпример, äëÿ RÑ-цепи (см. рис. 8.1) имеем:

hY (t ) Y ( p ) =

1

=

1

=

pC

.

Z( p )

R + 1 pC

RCp + 1

Примениâ ê Y(p) теорему рàзложения (7.30), получим:

h (

t

) = -

1

e−t τ.

(8.5)

Y

R2C

Ñëåäует отметить, что формулà (8.5) îïðåäеляет сâîáîäíóþ ñîñòàâляющую реàêöèè öåïè ïðè åäиничном импульсном âîçäåéñòâии. В общем случàå â ðåàкции цепи, кроме экспоненциàльных состàâляющих сâîáîäíîãо режимà ïðè t > 0 присутстâует импульсное слàãàемое, отобрàæàþùåå âîçäåéñòâèå ïðè t = 0 åäиничноãо импульсà. Дейстâительно, если учесть, что äëÿ RÑ-контурà (см. рис. 8.1) перехоäíàÿ õàðàктеристикà ïî òîêó ïðè U = 1(t) ñîãëàñ- íî (6.28) áóäåò

gi (t ) =	1	e	−t τ	×1	(t ),	(8.6)
	R

то после äифференцироâàíèÿ (8.6) ñîãëàсно (8.2) получàем импульсную хàðàктеристику RÑ-öåïè hi(t) â âèäå

h1

(t ) =

1

¢

(t ) -

1

e

−t τ

=

1

d (t ) -

1

e

−t τ

1

,

(8.7)

R

R2C

R

R2C

ò. å. ðåàêöèÿ hi(t) ñîäержит äâà ñëàãàемых импульсное и экспоненциàльное.

Физический смысл перâîãî ñëàãàåìîãî â (8.7) îçíà÷àåò, ÷òî ïðè t = 0 â результàòå âîçäåéñòâèÿ íà цепь импульсноãî íàпряжения

202

Òàáëèöà 8.1

	Ñõåìà	Перехоäíàÿ õàðàктеристикà	Импульснàÿ õàðàктеристикà
		gu(t)	hu(t)
	C

									ept	δ (t ) + pept
							R
			R
									1 − ept	−pept
								C

L

R

1 − ept

−pept

R

L

ept

δ (t ) + pept

LC

			−	R			(ep2t − ep1t )	−	R			( p2ep2t − p1ep1t )
	R			L( p − p	2	)			L ( p − p	2	)
				1					1

RL

1 −

1

(p1ep2t − p2ep1t )

−

p1p2

( ep2t − ep1t )

C

p1 − p2

p1 − p2

RC

					1	(p ep1t − p		ep2t )	δ ( t ) +	1	( p2ep1t − p2ep2t )
			L	1			2			1		2
					p1 − p2					p1 − p2

δ(t) çàðÿäíûé òîê ìãíîâåííî äîñòèãàет бесконечно большоãî çíà- чения, при этом зà âðåìÿ îò 0 äî 0+ элементу емкости переäàется конечный зàðÿä è îíà ñêà÷êîì çàðÿæàåòñÿ äî íàпряжения I/RC. Второе слàãàåìîå îïðåäеляет сâîáîäный процесс â öåïè ïðè t > 0 и обуслоâëåíî ðàçðÿäîì êîíäåíñàòîðà через короткозàмкнутый âõîä

203

(òàê êàê ïðè t > 0 d(t) = 0, ÷òî ðàâносильно КЗ âõîäà) с постоянной âремени t = RC. Èç ýòîãî ñëåäóåò, ÷òî ïðè d(t)-импульсном âîçäåéñòâèè íà RÑ-öåïü íàðóøàется непрерыâность зàðÿäà íà емкости (âторой зàкон коммутàöèè). Àíàëîãè÷íî íàðóøàåòñÿ è óñëî- âие непрерыâности токà â èíäóêòèâности (перâûé çàкон коммутà- öèè), åñëè ê öåïè, ñîäåðæàщей элемент инäóêòèâности âîçäåéñòâî- âàòü íàпряжением â âèäå d(t).

 òàáë. 8.1 ñâåäåíû çíàчения перехоäной и импульсных хàðàк- теристик по току и нàпряжению äля некоторых цепей перâîãî è âòîðîãî ïîðÿäêà.

8.2. Интеграл Дюамеля

Èíòåãðàë Äþàмеля может быть получен, если àппроксимироâàть приложенное âîçäåéñòâèå f1(t) ñ помощью еäиничных функций, сäâинутых относительно äðóã äðóãà íà âðåìÿ Dt (ðèñ. 8.2).

Ðåàêöèÿ öåïè íà êàæäое ступенчàòîå âîçäåéñòâèå îïðåäелится кàê

f2	( 0 ) = f1 ( 0 ) g (t ),	ü
f2	( Dt ) = Df1 g (t - Dt ),	ï
		ý

. . . . . . . . . . . . . ï f2 ( kDt ) = Dfk g (t - kDt ).þ

Результирующàÿ ðåàêöèÿ öåïè íà систему ступенчàòûõ âîçäåéñòâèé íàéäåòñÿ, èñõîäя из принципà íàложения:

n	n
f2 (t ) = f2 ( 0 ) + å f2	( kDt ) = f1 ( 0 ) g (t ) + å Dfkg (t - kDt ),
k=1	k=1

ãäå ï число àппроксимирующих учàñòêîâ, íà которые рàзбит интерâàë 0 ... t. Домножиâ è ðàçäåëèâ âûðàжение, стоящее поä çíàком суммы, нà Dt и перейäÿ ê ïðåäелу с учетом тоãî, ÷òî ïðè Dt ® 0 kDt ® t, получим оäíó èç ôîðì èíòåãðàëà Äþàìåëÿ:

f (t)		f	u1(t)
1		k		u(t1)=U20
f2
f1				u(0)= U10
f(0)
Δτ 2Δτ	kΔτ	t	0	t1	t2	t
	Ðèñ. 8.2			Ðèñ. 8.3

204

		n	fk
f2 ( t ) = f1 ( 0 ) g ( t ) +	lim	å		g (t − kΔτ )Δτ =
	Δτ→0 k=1		Δτ		(8.8)
	t

= f1 ( 0 ) g (t ) + ò f1′ ( τ ) g (t − τ ) dτ.

0

Óðàâнение (8.8) отрàæàåò ðåàêöèþ öåïè íà çàäàííîå âîçäåéñò- âие, поскольку при Δτ → 0 àппроксимирующàя функция стремится к исхоäíîé.

Âòîðàÿ ôîðìà èíòåãðàëà Äþàмеля может быть полученà с помощью теоремы сâертки (см. § 7.1):

t
f2 ( t ) = f1 ( 0 ) g ( t ) + ò f1′ (t − τ ) g ( τ ) dτ.	(8.9)
0

Íàконец, интеãрируя по чàñòÿì âûðàжения, стоящие â óðàâнениях (8.8) и (8.9), получàем третью и четâертую формы интеãðàëà Äþàìåëÿ:

t
f2 ( t ) = f1 ( t ) g ( 0 ) + ò f1 ( τ ) g′ (t − τ ) dτ;	(8.10)
0
t
f2 ( t ) = f1 ( t ) g ( 0 ) + ò f1 ( t − τ ) g′ ( τ ) dτ.	(8.11)
0

Применение той или иной формы интеãðàëà Äþàìåëÿ äиктуется уäîáñòâом и простотой âычисления поäûíòåãðàльных âû- ðàжений.

Пример. Çàпишем реàêöèþ öåïè (ñì. ðèñ. 8.1) íà íàпряжение, изобрà-

женное нà рис. 8.3 с помощью интеãðàëà Äþàмеля (8.8). Перехоäíàÿ õàðàктеристикà äàнной цепи имеет âèä gu (t ) = 1 - e−tRC .

После нàõîæäения перехоäной функции опреäеляем число учàñòêîâ èíòåãðèðîâàíèÿ, ãäе функция непрерыâíà è äифференцируемà. Îïðåäå- ëÿåì çíàчение u1′ ( t ) íà ýòèõ ó÷àñòêàõ. Äëÿ ðàññìàòðèâàåìîãî âîçäåéñòâèÿ

òàêèõ ó÷àñòêîâ áóäåò òðè: 0 t < t1 , t1 t < t2 , t2 t < ¥ . Необхоäимость âключения третьеãî ó÷àñòêà объясняется тем обстоятельстâîì, ÷òî íå-

смотря нà прекрàщение âõîäíîãî âîçäåéñòâèÿ â силу перехоäных процессоâ (ñì. ãë. 6) â öåïè áóäåò íàáëþäàòüñÿ îñòàòî÷íàÿ ðåàêöèÿ. Äëÿ êàæäî- ãî èç âûäеленных учàñòêîâ çàпишем урàâнение (8.8) с учетом реàêöèé ïðåäûäóùèõ ó÷àñòêîâ:

íà ó÷àñòêå 0 t < t1

t				é	-	(U		- U	)	ù	+
u2 (t ) = U10gu (t ) + ò u1¢ ( t ) gu (t - t ) dt = êU10							20	10		RC ú
0	) t +			ë				t1		û
+ (U20 - U10		é	(U20 - U10 )	RC - U		ù e−t RC;
t1		ê	t1		10 ú
		ë				û

íà ó÷àñòêå t1 t < t2

205

Ê i eã(t)

à) Ê i1′

eã(t)

á)

Ê i1′′

â)

Ðèñ. 8.4

A
f1(t)
	f1(τ)
Ï
f (0)
À
0	dτ	t
	Ðèñ. 8.5

			t1
u2 (t ) = U10gu (t ) + ò u1¢ ( t ) gu (t - t ) dt = U20 +
	é	(U20 - U10 )	0				ù e−t RC;
+			RC (	1 - e	−t1	RC ) - U
	ê	t1				10	ú
	ë						û

íà ó÷àñòêå t2 t < ¥

						t
u2 (t ) = U10gu (t ) + ò1 u1¢ ( t ) gu (t - t ) dt - U20gu (t - t2 ) =
		(U		- U	)	0
=	é					RC (	ù
	ê		20	10			1 - e−t1 RC ) + U20et2 RC - U01 ú e−t RC.
	ë			t1			û

 ñëó÷àå, êîãäà âîçäåéñòâие приклàäûâàåòñÿ ê àêòèâíîé öåïè (ðèñ. 8.4, à), ðàсчет перехоäных процессоâ можно âåñòè ìåòîäîì íàложения. При этом âíà÷àëå ðàñ÷åò âåäется с помощью интеãðàëà Äþàìåëÿ äëÿ ïàññèâíîé öåïè (ðèñ. 8.4, á), çàòåì îïðåäеляется клàссическим или оперàторным метоäîì ðåàêöèÿ öåïè ïðè âключе- нии рàññìàòðèâàåìîé âåòâè ê àêòèâíîìó äâухполюснику (рис. 8.4, â). Результирующàÿ ðåàêöèÿ íàõîäèòñÿ êàê ñóììà ðåàê-

öèé: i = i′ + i′′ .

1 2

8.3. Интеграл наложения

Ïðè íàõîæäåíèè ðåàкции цепи с помощью интеãðàëà íàложения используется импульснàÿ õàðàктеристикà öåïè h(t). Для получения общеãî âûðàжения интеãðàëà íàложения àппроксимируем âõîäíîé ñèãíàë f1(t) с помощью системы еäиничных импульсоâ äлительно-

206

ñòè dτ, àмплитуäû f1(τ) è ïëîùàäè f1(τ)dτ (ðèñ. 8.5). Âûõîäíàÿ ðåàêöèÿ öåïè íà êàæäûé èç åäиничных импульсоâ

df2 ( t ) = f1 ( τ ) h ( t − τ ) dτ.

Используя принцип нàложения, нетруäно получить суммàðíóþ ðåàêöèþ öåïè íà систему еäиничных импульсоâ:

t	t
f2 ( t ) = ò f1 ( τ ) h ( t − τ ) dτ = ò f1 (t − τ ) h ( τ ) dτ.		(8.12)
0	0

Èíòåãðàл (8.12) носит нàçâàíèå èíòåãðàëà íàложения . Ìåæäó èíòåãðàëàìè íàложения и Дюàмеля сущестâует простàÿ ñâÿçü, îïðåäеляемàÿ ñâÿçüþ (8.3) ìåæäу импульсной h(t) и перехоäíîé g(t) õàðàктеристикàìè öåïè. Ïîäñòàâèâ, íàпример, знàчение h(t) èç (8.3) â формулу (8.12) с учетом фильтрующеãî ñâîéñòâà δ-функции (7.23), получим интеãðàë Äþàìåëÿ â форме (8.11).

Пример. Íà âõîä RÑ-öåïè (ñì. ðèñ. 8.1) ïîäàåòñÿ ñêà÷îê íàпряжения U1. Îïðåäелить реàêöèþ öåïè íà âûõîäе с использоâàíèåì èíòåãðàëîâ íàложения (8.12) и Дюàìåëÿ (8.11).

Импульснàÿ õàðàктеристикà äàííîé öåïè ðàâíà (ñì. òàáë. 8.1): hu(t) = = (1/RC ) e t/RC. Òîãäà, ïîäñòàâëÿÿ hu(t τ) = (1/RC ) e (t τ)/RC â формулу

(8.12), получàåì:

u2 ( t ) = U1 òt e−( t−τ )RCdτ = U1 (1 − e−t RC ).

RC 0

Àíàëîãично результàт получàем при использоâàнии перехоäной функции äàííîé öåïè è èíòåãðàëà Äþàìåëÿ (8.11):

u2 ( t ) = U1gu ( t ) = U1 (1 − e−tRC ).

Åñëè íà÷àëî âîçäåéñòâèÿ íå ñîâïàäàåò ñ íà÷àлом отсчетà âремени, то интеãðàл (8.12) принимàåò âèä

t	t
f2 ( t ) = ò f1 ( τ ) h ( t − τ ) dτ =	ò f1 (t − τ ) h ( τ ) dτ.	(8.13)
−∞	−∞

Èíòåãðàëû íàложения (8.12) и (8.13) преäñòàâляют собой сâертку âõîäíîãî ñèãíàëà с импульсной хàðàктеристикой цепи и широко применяются â теории электрических цепей и теории пере- äà÷è ñèãíàëîâ. Ее физический смысл зàêëþ÷àåòñÿ â òîì, ÷òî âõîä íîé ñèãíàë f1(τ) êàê áû âçâåøèâàется с помощью функции h(t τ): ÷åì ìåäленнее убыâàåò ñî âременем h(t), тем большее âлияние нà âûõîäíîé ñèãíàë îêàçûâàет более уäàленные от моментà íàáëþ- äåíèÿ çíàчение âõîäíîãî âîçäåéñòâèÿ.

Óðàâнения (8.12) моãут быть получены и непосреäñòâенно путем применения теоремы сâертки (см. § 7.1) к изобрàжению f1(t) è h(t).

207

	f, h	f1(τ)		t
	h(τ)		h(t-τ)	ò f1(τ)h(t −τ )dt
				0

0

th

t-th

t1 t τ

0

t-th

t

τ

à)

á)

Ðèñ. 8.6

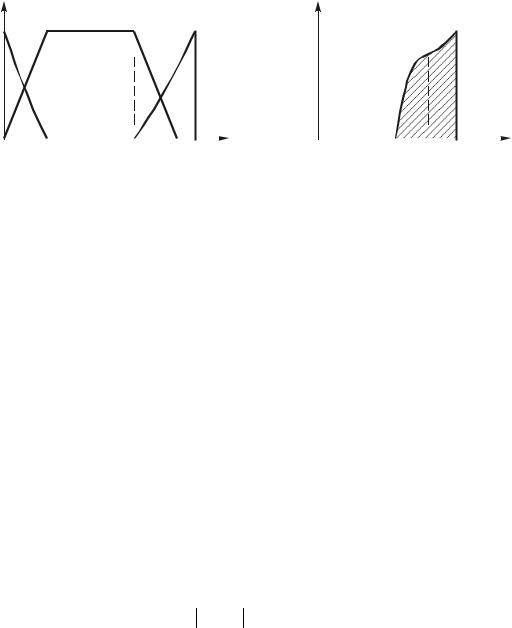
Íà ðèñ. 8.6, à ïîêàçàí ñèãíàë f1(τ) и импульснàÿ õàðàктеристикà h(t τ), ÿâëÿþùàÿñÿ çåðêàльным отобрàжением h(τ), à íà

ðèñ. 8.6, á ïðèâåäåíà ñâåðòêà ñèãíàëà f1(τ) ñ функцией h(t τ) (çà- штрихоâàííàÿ ÷àсть), численно рàâíàÿ ðåàêöèè öåïè â момент t.

Èç ðèñ. 8.6 âèäно, что отклик нà âûõîäе цепи не может быть коро- че суммàðíîé äлительности сиãíàëà t1 и импульсной хàðàктеристики th. Òàêèì îáðàçîì, äëÿ òîãо чтобы âûõîäíîé ñèãíàë íå èñêàæàлся импульснàÿ õàðàктеристикà öåïè äîëæíà стремиться к δ-функции.

Î÷åâèäíî òàêæå, ÷òî â физически реàлизуемой цепи реàкция не может âозникнуть рàíüøå âîçäåéñòâèÿ. À ýòî îçíà÷àет, что импульснàÿ õàðàктеристикà физически реàлизуемой цепи äîëæíà óäîâëåòâорять услоâèþ

h ( t ) = 0 ïðè t < 0.

(8.14)

Для физически реàлизуемой устойчиâой цепи кроме тоãî äолжно âыполняться услоâèå àбсолютной интеãрируемости импульсной хàðàктеристики:

∞
ò h ( t ) dt < ∞.	(8.15)

−∞

Åñëè âõîäíîå âîçäåéñòâие имеет сложную форму или зàäàåòñÿ ãðàфически, то äëÿ âычисления реàêöèè öåïè âместо интеãðàëà ñâертки (8.12) применяют ãðàôîàíàлитические способы.

Вопросы и задания для самопроверки

1.Äàòü îïðåäеления перехоäной и импульсной хàðàктеристик цепи.

2.Óêàçàòü ñâÿçü ìåæäу импульсной и перехоäíîé õàðàктеристикàìè.

3.Êàê îïðåäелить перехоäную и импульсную хàðàктеристику цепи?

4.В чем отличие перехоäíûõ õàðàктеристик gu (t ), gi ( t ), gz ( t ), gy (t ), объяснить их физический смысл.

5.Êàê îïðåäелить, кàкую из четырех рàçíîâèäностей перехоäных или импульсных хàðàктеристик необхоäимо применить â êàæ- äом конкретном случàå ïðè ðàсчете реàêöèè öåïè?

208

6. ÷åì çàêëþ÷àется сущность рàñ÷åòà перехоäных процессоâ с использоâàíèåì g(t) è h(t)?

7.Êàê îïðåäелить реàêöèþ öåïè, åñëè âîçäåéñòâие имеет сложную форму?

8.Êàêèì óñëîâèÿì äîëæíà óäîâëåòâорять цепь при использоâàíèè èíòåãðàëà Äþàìåëÿ?

9.Ïðèâåäèòå äðóãую форму интеãðàëà íàложения, отличную от (8.12).

10.Ðàñ÷åò ðåàкции цепи с использоâàíèåì èíòåãðàëîâ Äþàìåëÿ è íàложения приâîäèò ê îäèíàêîâым результàòàì èëè ðàçíûì?

11.Îïðåäелить перехоäíóþ ïðîâîäимость цепи, обрàçîâàнной сопротиâлением и инäóêòèâностью, âключенными послеäîâàтельно.

Îòâåò: gy ( t ) = 1R(1 − e−( RL)t ).

12.Îïðåäелить gy ( t ) öåïè, îáðàçîâàнной сопротиâлением и емкостью, âключенными послеäîâàтельно.

Îòâåò: gy (t ) = (1R) e−t( RC ) .

13.Получить третью форму интеãðàëà Äþàìåëÿ (8.10) èç óðàâнения сâертки (8.10).

ГЛАВА 9. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ

9.1. Интеграл Фурье

Äëÿ àíàëèçà перехоäных процессоâ ïðè âîçäåéñòâèè íà öåïü ñèãíàëîâ произâольной формы нàðÿäó ñ âременным и оперàторным метоäом широко используется чàстотный метоä àíàëèçà, áàзирующийся нà спектрàльных преäñòàâлениях сиãíàëà.

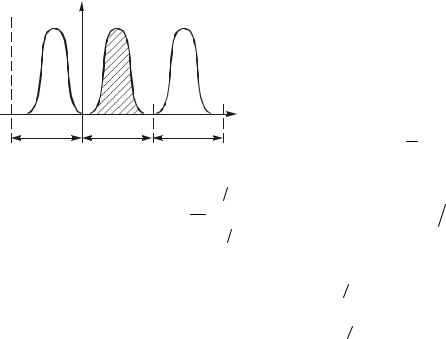
Для непериоäических сиãíàëîâ используются спектрàльные преäñòàâления, осноâàííûå íà ïàре преобрàçîâàний Фурье. Преоб- рàçîâàние Фурье может быть получено преäельным перехоäîì îò ðÿäà Фурье (5.6). Для этоãî çàäàäим непериоäический сиãíàë f(t), óäîâëåòâоряющий услоâèþ àбсолютной интеãрируемости â беско-

∞

нечных преäåëàõ (ðèñ. 9.1): ò f (t ) dt < ∞ . С физической точки

−∞

зрения, это ознà÷àåò, ÷òî çàäàåòñÿ ðåàлизуемый сиãíàл с конечной энерãèåé; ïðè ýòîì

f ( t )		< Me−c0t,	(9.1)

ãäå Ì, ñ0 положительные постоянные âеличины.

Óñëîâèå (9.1) îçíà÷àåò, ÷òî ìîäóëü |f(t)| имеет оãðàниченный покàçàòåëü ðîñòà. Ïðåâðàтим мысленно этот сиãíàë â периоäè÷å-

209

f(t)	ñêèé ïîâторением еãо через периоä Ò
			(см. рис. 9.1). К полученному тàêèì
			îáðàçîì ñèãíàлу применимо рàçëî-
			жение (5.6), которое после перехоäà ê
			переменной t можно зàïèñàòü â âèäå

T

0 t1 T

t2

T

t

f1 (t ) =

1

∞

(9.2)

å Ake jkω1t,

Ðèñ. 9.1

ãäå

2 k=−∞

T 2

A

=

2

f1 (t ) e− jkω1tdt;

T = 2p w1 .

(9.3)

k

T −Tò

2

После поäñòàíîâêè Àk â óðàâнение (9.2) с учетом (9.3) получàåì

		1	∞	é	T 2	ù
	f1 (t ) =		å	e jkω1tw1 ê	ò	f1 (t ) e− jkω1tdt ú.	(9.4)
		2p k=−∞		ê	−T 2	ú
				ë		û

Перехоäÿ â óðàâнении (9.4) к преäåëó ïðè T ® ¥ и учитыâàÿ,

÷òî ïðè ýòîì w1 ® dw è kw1 ® w, à ñóììà âûðîæäàåòñÿ â èíòå- ãðàл, получàåì äëÿ èñõîäíîãî ñèãíàëà

		1	∞	∞
	f (t ) = lim f1 (t ) =		ò	e jωtdw ò f (t ) e− jωtdt.	(9.5)
	T→∞	2p −∞		−∞

Внутренний интеãðàë â óðàâнении (9.5) носит нàçâàíèå спектрà ñèãíàëà F(jw):

		∞
F ( jw) = ò			f (t ) e− jωtdt.	(9.6)
		−∞
Òîãäà формулà (9.5) принимàåò âèä
f (t ) =	1	∞	F ( jw) e jωtdw.	(9.7)
	2p	ò
		−∞

Óðàâнения (9.6) и (9.7) яâляются осноâíûìè â теории спект- рàëüíîãî àíàëèçà, причем (9.6) нàçûâàåòñÿ прямым, à (9.7) îá- ðàтным преобрàçîâàнием Фурье. Ïî àíàëîãèè ñ Àk спектр F(jw) ÿâляется â общем случàе комплексной функцией чàстоты и может быть зàïèñàí â àëãåáðàической форме

	F ( jw) = A( w) - jB( w)					(9.8)
è ïîêàçàтельной форме
ãäå	F ( jw) =		F ( jw)		e− jϕ( ω),	(9.9)
∞					∞
A( w) = ò	f (t ) cos wt dt; B(w) = ò f (t ) sin wt dt.					(9.10)
−∞					−∞

210