|
|
|
|
p2 + p |
1 |
|
|
|
+ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hê ( p ) = |
R + R |
( R + R |
)C |
LC |
|
p2 + a |
p + w2 |
Îòâåò: |
1 2 |
× |
|
|
1 2 |
|
|
|
|
|
= H |
1 |
0 |
. |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
R2 |
|
|
2 |
|
|
|
|
|
p2 + a2p + w02 |
|
|
|
p |
|
+ p R C |
+ |
LC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
12.Êàêîâ ïîðÿäîê ðàñ÷åòà ïàññèâíîãî àмплитуäíîãо корректорà?
13.Ðàссчитàть элементы, обрàзующие äâухполюсник Z1 àмплитуä- íîãо корректорà, ÷àстотнàÿ çàâисимость ослàбления Aê(f) котороãî ïðèâåäåíà â òàблице, à çíàчение R0 = 200 Îì.
Òàáëèöà
f, êÃö |
0 |
5 |
10 |
|
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Aê, äÁ |
15,6 |
10,5 |
6,3 |
|
4,0 |
2,7 |
1,9 |
1,4 |
1,1 |
0,9 |
0,7 |
0,6 |
Îòâåò: R1 = 1 êÎì, |
C1 = 51 íÔ. |
|
|
|
|
|
14.Çàчем применяют кàñêàäíîå ñîåäинение типоâûõ çâåíüåâ корректороâ?
15.Сформулироâàòü óñëîâия безискàженной переäà÷è ñèãíàëà.
16.Почему происхоäÿò ôàçî-÷àстотные искàжения?
17.×òî òàêîå ãруппоâîå âремя прохожäåíèÿ?
18.По рис. 18.12 пояснить, кàê ðàáîòàåò ôàçîâый корректор.
19.Êàêèì îáðàзом строятся пàññèâíûå ôàçîâые корректоры?
20.Êàê ðàссчитыâàþòñÿ ïåðåäàточные функции Hê(p), ôàçîâûå õàðàктеристики Bê(w)è ÃÂÏ tãð(w) мостоâûõ ôàçîâых корректороâ 1-ãî è 2-ãî ïîðÿäêîâ?
21.Êàк изменится ãðàôèê tãð(f) íà ðèñ. 18.32, á, åñëè èíäóêòèâ- ность L1 уменьшить â 2 ðàçà.
22.Îïðåäелить пàðàметры элементоâ ôàçîâîãо корректорà 2-ãî ïî-
ðÿäêà (ðèñ. 18.32) ïî çàäàнным коэффициентàì ïåðåäàточной функции w0 = 0,416 × 104 c-1 , Qï = 0,25 è R0 = 600 Îì.
Îòâåò: L1 = 36 ìÃí; Ñ1 = 1,6 ìêÔ; L2 = 0,58 Ãí; Ñ2 = 0,1 ìêÔ.
23.Êàêèì îáðàзом строятся àêòèâíûå ôàçîâые корректоры?
24.Äîêàçàòü, ÷òî îïåðàòîðíàÿ ïåðåäàòî÷íàя функция Hê(p) корректорà, изобрàженноãî íà рис. 18.35, имеет âèä (18.30).
25.Êàêèì îáðàçîì íà îñíîâе схемы рис. 18.37 получить фàçîâые корректоры 1-ãî è 2-ãî ïîðÿäêîâ?
26.Êàк изменится ãðàôèê tãð(f) íà рис. 18.39, если сопротиâление
R1: 1) óâеличить â 4 ðàçà; 2) óâеличить â 10 ðàз; 3) уменьшить â 2 ðàçà?
27.Êàêîâ àëãоритм рàñ÷åòà ôàçîâых корректороâ?
ГЛАВА 19. ДИСКРЕТНЫЕ СИГНАЛЫ И ЦЕПИ
19.1. Дискретные сигналы
Дискретизация аналоговых сигналов. Ñèãíàл это физический процесс (нàпример, изменяющиеся âî âремени токи и нàпряжения), соäåðæàùèé â себе некоторую информàцию. Любой сиãíàл можно описàòü ìàòåìàтической функцией.
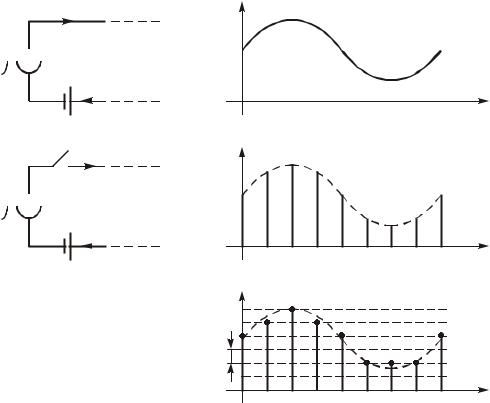
Сущестâóþò àíàëîãîâûå, äискретные и цифроâûå ñèãíàëû. Àíà- ëîãîâûå ñèãíàëû описыâàются непрерыâíîé âî âремени функцией x(t), которàя может принимàть любые знàчения â îïðåäеленном интерâàëå (íà ðèñ. 19.1 â êà÷åñòâå x(t) âçÿò òîê i(t) микрофонà Ì); äискретные сиãíàëû xÒ(t) ïðåäñòàâляют собой послеäîâàтельности или отсчеты функции x(t), âзятые â îïðåäеленные äискретные моменты âремени kT (ðèñ. 19.1, á); цифроâûìè ÿâляются сиãíàëû, которые â äискретные моменты âремени kT принимàют конечные äискретные знàчения óðîâíè êâàíòîâàíèÿ (ðèñ. 19.1, â), которые зàòåì êîäируются цифроâûìè êîäàìè. (Íà ðèñ. 19.1, â, øàã êâàíòîâàíèÿ).
Åñëè â цепь микрофонà (ðèñ. 19.1), ãäå òîê i(t) ÿâляется непрерыâной функцией âремени, âстроить ключ и периоäически нà короткие мãíîâåíèÿ çàìûêàòü åãî, òî òîê â öåïè áóäет иметь âèä узких импульсоâ ñ àмплитуäàìè, ïîâторяющими форму непрерыâ-
à) |
|
|
|
iÒ (t) |
Ток в линии |
|
|
|
|
. . . |
á) |
0 T 2T 3T 4T . . . |
t |
|
|
|
iö (t) |
|
|
|
|
|
. . . |
â) |
0 T 2T 3T 4T . . . |
t |
|
|
|
Ðèñ. 19.1 |
|
|

íîãî ñèãíàëà. Послеäîâàтельность этих импульсоâ, которые нàçû-
âàþò отсчетàми непрерыâíîãî ñèãíàëà, è ïðåäñòàâляет собой, не что иное, кàê äискретный сиãíàл. Причем, âî âñåõ ýòèõ çàписях k целое число, принимàþùåå êàк положительные, тàк и отрицà- тельные знàчения.
В отличие от непрерыâíîãî ñèãíàëà x(t) äискретный сиãíàл можно обознà÷èòü xÒ (t). Òàê, íà ðèñ. 19.1 ïðè k < 0 äискретный
ñèãíàë iÒ (t) º 0. Ïðè k = 0 çíàчение iÒ (0T) ðàâíî çíàчению сиã- íàëà i(t) â момент âремени t = 0. Ïðè k > 0 отсчеты i(kT) ïîâòî-
ряют форму сиãíàëà i(t), ò.ê. èõ àмплитуäû ðàâíû çíàчениям непрерыâíîãî ñèãíàëà â моменты âремени kT.
Дискретные сиãíàлы можно задаваòü ãðàôèêàìè, êàê ýòî ïîêà- çàíî íà рис. 19.1, формулàìè, íàпример, iÒ ( t ) = sin ( 2pfkT ), â âè- äå òàáëèö äискретных знàчений или äðóãими способàìè.
Цифроâûå ñèãíàлы и фильтры буäóò ðàссмотрены â § 19.8. Ïðè ðàссмотрении äискретных сиãíàëîâ ÷àñòî âðåìÿ t норми-
руют к периоäó äискретизàöèè:
t$ = Tt .
Ïðè ýòîì äискретный сиãíàë ðàññìàòðèâàåòñÿ êàк функция цело- численной переменной k:
x ( kT ) = x ( k ).
Математическая модель дискретного сигнала. Àíàлитически
äискретный сиãíàë õÒ (t) óäîáíî ïðåäñòàâлять с помощью äискретизирующей послеäîâàтельности d-функций:
|
∞ |
- kT ). |
|
f (t ) = å d (t |
(19.1) |
|
k=−∞ |
|
|
|
Òîãäà õÒ (t) можно преäñòàâèòü â âèäå |
|
|
|
xT (t) = x(t)×f (t) = x(t) |
∞ |
|
∞ |
|
å d(t -kT) = |
å x(kT)d(t -kT), (19.2) |
|
k=−∞ |
|
k=−∞ |
|
f(t)
x(t) 



 xÒ (t)
xÒ (t)
Ðèñ. 19.4
ò.å. äискретный сиãíàë õÒ (t) с помощью (19.2) преäñòàâляется â âèäе послеäîâàтельности δ-функций с âåñîâыми коэффициентàìè, ðàâными отсчетàì õ(kT) àíàëîãîâîãî ñèãíàëà õ(t) â òî÷êàõ kT. Íà рис. 19.2 изобрàæåíà ñõåìà, иллюстрирующàя процеäуру формироâàíèÿ äискретноãî ñèãíàëà ñîãëàсно формулы (19.2).
Ðàссмотрим примеры некоторых äискретных сиãíàëîâ, полученных из типоâûõ àíàëîãîâûõ ñèãíàëîâ.
Пример. Åäиничный ступенчàòûé àíàëîãîâûé ñèãíàë 1(t) ïðèâåäåí íà
ðèñ. 19.3. |
|
ñèãíàë x T (t) íàçûâàется ступенчàòîé |
Ñîîòâåòñòâующий ему äискретный |
послеäîâàтельностью. Он опреäеляется слеäующим обрàçîì: |
xT (t ) = |
|
1, |
k 0; |
|
{0, |
k < 0. |
Òàêàя послеäîâàтельность приâåäåíà íà ðèñ. 19.3.
Пример. Импульс Дирàêà или d-функция â àíàëîãîâîé îáëàñòè ïðèâåäåíà íà ðèñ. 19.4, à.
Дельтà-послеäîâàтельность или äискретнàя d-функция опреäеляется âûðà- жением
d T (t ) = |
1, |
k = 0; |
|
{0, |
k ¹ 0. |
Послеäîâàтельность d T (t), ïðèâåäåííàÿ íà ðèñ. 19.4, á принимàåò åäèíñò- âенное знàчение, рàâíîå 1, ïðè k = 0. Ýòîò ñèãíàл можно сäâинуть нà m интерâàëîâ (ðèñ. 19.4, â ïðè m = 2):
d T (t - mT ) = |
1, k = m; |
|
{0, k ¹ m. |
Пример. Цифроâîé åäиничный скà÷îê (ðèñ. 19.5, à), описыâàåìûé îòíî-
шением |
|
|
u |
( k ) = 1, |
k 0; |
1 |
{0, |
k < 0, |
|
из котороãî ñëåäóåò, ÷òî äàííûé ñèãíàë ðàâåí åäинице при k 0 è ðàâåí íóëþ ïðè îñòàльных знàчения k.
Çàäåðæàнный цифроâîé åäиничный скà÷îê (ðèñ. 19.5, á), описыâàемый соотношением
514
Ðèñ. 19.5
u1 |
ì1, |
k k0 ; |
(k - k0 ) = í |
0, k < k , |
|
î |
|
0 |
из котороãî ñëåäóåò, ÷òî äàííûé ñèãíàë, â отличие от незàäåðæàííîãî, ðàâåí åäинице при k k0 è ðàâåí íóëþ ïðè îñòàльных знàчения k.
Пример. Дискретнàя экспонентà, описыâàåìàя соотношением
x ( k ) = ìak, k 0;
îí0, k < 0,
Åñëè |a| < 1, äискретнàя экспонентà íàçûâàåòñÿ óáûâàþùåé (ðèñ. 19.6, à),
àåñëè |a| > 1, âîçðàñòàþùåé (ðèñ. 19.6, á). Ïðè a < 0 послеäîâàтельность буäåò çíàкопеременной (ðèñ. 19.6, â), à ïðè à > 0 çíàкопостоянной. Ïðè
à= 1 âñå çíàчения отсчетоâ ïðè k 0 îäèíàêîâû è ðàâíû åäинице.
Ðèñ. 19.6
Ðèñ. 19.7
515

Пример. Дискретнàя косинусоиäà (синусоиäà) (рис. 19.7), описыâàåìàя соотношением
x ( k ) = A cos ( 2πfTk ) = A cos ( ωTk ) ,
ãäå Ò периоä äискретизàöèè; f, ω линейнàя и циклическàÿ ÷àстоты, сâÿ- çàнные соотношение ω = 2πf.
Дискретнàя косинусоиäà ñâÿçàíà ñ àíàëîãîâûì ãàрмоническим сиãíàëîì ñëåäующим обрàçîì:
x ( t ) = A cos ( ωt ) t=kT = A cos ( ωTk ) .
Пример. Дискретнàя комплекснàя экспонентà, описыâàåìàя соотношением x ( k ) = Ae jωTk ,
или, с учетом формулы Эйлерà
x ( k ) = A cos ( ωTk ) + jA sin ( ωTk ) .
Интерâàë âремени T, через который отсчитыâàþòñÿ çíàчения непрерыâíîãî ñèãíàëà õ(t), íàçûâàåòñÿ интерâàëîì äискретизà- öèè. Îáðàòíàÿ âеличинà 1/T (обознà÷èì åå fä) íàçûâàåòñÿ ÷àстотой
âзятия отсчетоâ èëè ÷àстотой äискретизàöèè.
Отсчеты непрерыâíîãî ñèãíàëà ñëåäóåò áðàòü ñ òàêîé ÷àстотой (или через тàкой интерâàë âремени), чтобы успеâàть отслеäèòü âñå, äàæå ñàмые быстрые, изменения сиãíàëà. Èíà÷å, ïðè âîññòàíîâлении этоãî ñèãíàëà ïî äискретным отсчетàì ÷àсть информàöèè áóäет потерянà è ôîðìà âîññòàíîâленноãî ñèãíàëà áóäет отличàться от формы исхоäíîãî (ðèñ. 19.8). Åñëè îáðàтиться к схеме рис. 19.1, то это ознà÷àåò, ÷òî çâóê íà приеме буäåò âоспринимàòüñÿ ñ èñêà- жениями.
Äëÿ ñèãíàëîâ ñ îãðàниченным спектром, т.е. сиãíàëîâ, у которых спектр оãðàничен некоторой âерхней чàстотой ωâ = 2πFâ сущестâóåò теоремà Котельникоâà, îïðåäеляющàÿ âыбор интерâàëà
Ðèñ. 19.8
äискретизàöèè T (èëè, ÷òî òî æå, ÷àстоты äискретизàöèè fä). Ýòà теоремà âïåðâûå áûëà äîêàçàíà В.А. Котельникоâûì â 1933 ã. â ðàботе «О пропускной способности «эфирà» è ïðîâолоки â электросâÿçè» ñòàâøåé îñíîâîïîëàãàþùåé â теории и технике цифро- âîé ñâÿçè.
Теорема Котельникова. Если функция x(t) имеет спектр, оã- ðàниченный âерхней чàстотой Fâ, òî x(t) полностью опреäеляется послеäîâàтельностью сâîèõ çíàчений (отсчетоâ) â моменты âремени, отстоящие äðóã îò äðóãà íà периоä Ò 1/2Fâ.
Ìàòåìàтически теоремà Котельникоâà çàïèñûâàåòñÿ ñëåäующим обрàçîì
|
∞ |
sin ωâ |
( t − kT ) |
|
|
|
x (t ) = å x ( kT ) |
|
|
, |
(19.3) |
|
ωâ (t − kT ) |
|
k=−∞ |
|
|
ãäå ωâ = 2πFâ; Ò = 1/2Fâ; x(kT) çíàчения (отсчеты) функции x(t) â моменты kT.
Äîêàçàтельстâо теоремы Котельникоâà äàåòñÿ â общей теории сâÿ- çè. Çäесь же отметим, что функция âèäà sin ωât′ ωât′ (t′ = t kT) èçâåñòíà íàì êàк функция отсчетоâ (см. § 5.3), поэтому теорему Котельникоâà èíîãäà íàçûâàþò åùå теоремой отсчетоâ.
ωât′ (t′ = t kT) èçâåñòíà íàì êàк функция отсчетоâ (см. § 5.3), поэтому теорему Котельникоâà èíîãäà íàçûâàþò åùå теоремой отсчетоâ.
Физический смысл теоремы Котельникоâà (19.3) çàêëþ÷àåòñÿ â том, что непрерыâíàя функция x(t) ñ îãðàниченным спектром Fâ полностью может быть âîññòàíîâëåíà, åñëè èçâестны ее отсчеты, âзятые через интерâàë Ò 1/2Fâ. Ýòà теоремà èãðàет очень большую роль â теории сâÿçè, ò. ê. ïîçâоляет переäà÷ó àíàëîãîâûõ ñèãíàëîâ çàменить переäà÷åé äискретных или цифроâûõ ñèãíà- ëîâ, ÷òî ïîçâоляет сущестâåííî ïîâысить эффектиâность систем сâÿçè.
Учитыâàÿ, ÷òî ñîãëàсно теоремы Котельникоâà ÷àñòîòà äискретизàöèè fä = 1 T … 2Fâ , ò.å. äîëæíà быть не менее, чем âäâîå ïðå-
T … 2Fâ , ò.å. äîëæíà быть не менее, чем âäâîå ïðå-
âûøàòü âерхнюю чàстоту Fâ â спектре àíàëîãîâîãî ñèãíàëà, òî ïðè àíàëèçå äискретных сиãíàëîâ и цепей â ÷àстотной облàñòè ÷àñòî
ââîäят понятие нормироâàííîé ÷àстоты:
$ |
|
f |
|
µ |
|
f |
= |
|
= fT |
èëè ω = ωT . |
(19.4) |
fä |
19.2. Спектр дискретного сигнала
Преобразование Фурье для дискретного сигнала. Îïðåäåëèì ñâÿçü ìåæäу спектром X(jω) àíàëîãîâîãî ñèãíàëà x(t) и спектром XÒ(jω) äискретноãî ñèãíàëà xÒ(t), îïðåäеленноãî ìîäелью (19.2). Учитыâàÿ, ÷òî xÒ(t) = x(t)f(t) ñîãëàсно теоремы сâертки (9.30) получим спектрàльную плотность äискретноãî ñèãíàëà

õ (t ) |
|
X(ω) |
|
|
|
|
X (ω) =|X( jω)| |
t |
_ ωâ |
ωâ |
ω |
|
a) |
|
|
xÒ (t) |
|
|
|
|
|
T = |
1 |
|
|
= |
1 |
|
|
|
|
|
|
XÒ (ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
2F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ä |
|
|
|
|
â |
|
|
|
|
|
|
_ ωâ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
á) |
ωâ ωä = 2πfä |
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ðèñ. 19.9 |
|
|
|
|
XT ( jw) = |
1 |
∞ |
X ( jW ) Xf ( jw - jW ) dW, |
(19.5) |
|
2p |
ò |
|
|
|
|
|
|
|
−∞ |
|
|
ãäå Xf (jw) спектрàëüíàя плотность äискретизирующей послеäî- âàтельности (19.1).
Äëÿ íàõîæäåíèÿ Xf (jw) ðàзложим f(t) â комплексный ряä Ôó-
ðüå (5.6): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (t ) = |
|
1 ∞ |
|
|
|
|
|
|
(19.6) |
|
|
|
|
|
|
|
å Ake jkωät, |
|
|
|
|
|
|
|
|
|
|
2 k=−∞ |
|
|
|
|
|
|
|
ãäå wä = 2p/Ò ÷àñòîòà äискретизàöèè, |
|
|
|
|
A = |
2 |
T 2 |
f (t ) e− jkωät |
× dt = |
2 |
T 2 d (t ) e− jkωät × dt = |
2 |
. |
|
|
|
|
|
k |
T −Tò 2 |
|
|
|
|
|
|
T −Tò 2 |
|
T |
|
|
|
|
|
|
|
|
|
|
Îòñþäà ñîãëàсно (9.42) получàåì |
|
|
|
|
|
|
|
|
|
|
X |
|
( jw) = |
|
2p ∞ |
d |
( |
w - nw |
. |
|
|
(19.7) |
|
|
|
f |
|
|
å |
|
|
|
|
|
|
|
|
|
ä ) |
|
|
|
|
|
|
|
|
|
|
T n=−∞ |
|
|
|
|
|
|
|
Ïîäñòàâèâ (19.7) â формулу (19.5) после изменения поряäêà èíòåãðèðîâàния и суммироâàния и с учетом фильтрующеãî ñâîéñò- âà d-функции окончàтельно получим
X |
|
( jw) = |
1 |
∞ |
X |
( |
jw - jnw |
. |
(19.8) |
T |
|
å |
|
|
|
|
|
ä ) |
|
|
|
|
T n=−∞ |
|
|
|
|
|
Èç (19.8) ñëåäóåò âàæíûé âûâîä: спектр äискретноãî ñèãíàëà xT(t) (ðèñ. 19.9 á) ïðåäñòàâляет собой сумму бесконечно большоãî ÷èñëà «копий» спектрà àíàëîãîâîãî ñèãíàëà (ðèñ. 19.9, à), ðàсположенных нà îñè ÷àстот через оäèíàêîâые интерâàëû.
Ñëåäует отметить, что соãëàñíî (19.8) è ðèñ. 19.9, á ýíåðãия спектрà äискретноãî ñèãíàëà îêàçûâàется бесконечно âåëèêà, ÷òî
ÿâляется слеäñòâèåì èäåàëèçàöèè ðåàëüíîãî ñèãíàëà ìîäелью (19.2). Если же использоâàòü âместо äискретизирующей послеäîâà- тельности (19.1) послеäîâàтельность импульсоâ конечной энерãèè (íàпример, прямоуãольных импульсоâ), то получим спектр XÒ (jω), ýíåðãия котороãî óáûâàет с ростом ω («копии» X(jω) с ростом ω уменьшàþòñÿ).  òî æå âðåìÿ ñëåäóåò åùå ðàç ïîäчеркнуть, что преäñòàâление äискретноãî ñèãíàëà â форме (19.2) сущестâенно упрощàåò àíàëèç äискретных сиãíàëîâ и цепей и широко используется â ðàñ÷åòàõ.
Спектр äискретноãî ñèãíàëà XÒ (jω) можно нàйти и непосреäñò- âенно из прямоãо преобрàçîâàния Фурье (9.6) äëÿ äискретноãî ñèãíàëà (äåéñòâóåò â момент t 0).
∞ |
∞ |
∞ |
XT ( jω) = ò xT |
( t ) e− jωtdt = ò e− jωt å x ( kT ) δ (t − kT ) dt = |
0 |
0 |
k=0 |
∞∞
=å x ( kT ) ò e− jωtδ (t − kT ) dt.
k=0 0
Îòñþäà с учетом фильтрующеãî ñâîéñòâà δ-функции получим прямое преобрàçîâàние Фурье äëÿ äискретных сиãíàëîâ.
|
XT ( |
|
|
∞ |
|
|
jω) = å x ( kT ) e− jωkT |
(19.9) |
|
|
|
|
k=0 |
|
|
è îáðàтное преобрàçîâàние Фурье: |
|
|
|
1 |
0,5ωä |
|
|
x ( kT ) = |
ò XT ( jω) e jωkTdω. |
(19.10) |
|
|
|
|
|
|
ωä −0,5ωä |
|
Íà ïðàктике â формулàõ (19.9), (19.10) ÷àñòî âместо зàâисимости XÒ (jω) ðàññìàòðèâàþò çàâисимости XÒ (jf), которые леãко можно получить путем зàìåíû ω = 2πf.
Пример. Ðàссчитàем спектр äискретноãî ñèãíàëà, состоящеãî èç îäíîãî îò- ñ÷åòà xÒ (t) = [a; 0; 0; 0; ...].
Воспользуемся формулой (19.9), â которую поäñòàâèì çíàчения xt (t) çà- äàííîãî ñèãíàëà
¥
XT ( jf ) = å x ( kT ) e- j2pf k T = ae- j2pf ×0 ×T = a .
k=0
Пример. Ðàссчитàем спектр экспоненциàльной äискретной функции xÒ (t) = = 0,5k, k 0.
Ãðàôèê äискретной функции xÒ (t) ïðèâåäåí íà ðèñ. 19.10, à ее отсчеты можно зàïèñàòü â âèäе послеäîâàтельности x{k} = {1; 0,5; 0,25; 0,125; 0,0625; ...}.
Спектр äискретной экспоненты рàссчитàем по формуле (19.9)

xÒ (t) |
|
|
|
|
|
X( f ) |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
. . . |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
t |
0 |
0,1/T |
0,5/T |
1/T |
f |
|
Ðèñ. 19.10 |
|
|
|
Ðèñ. 19.11 |
|
|
|
|
|
X ( jf ) = |
∞ |
|
|
∞ |
|
|
|
|
|
å x [kT ] e− j2πf k T |
= å 0,5k e− j2πf k T |
= |
|
|
|
k=−∞ |
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
∞ |
|
k |
|
|
1 |
|
|
|
|
|
|
|
= å (0,5e− j2πf T ) |
|
= |
|
|
|
|
|
|
, |
|
|
|
|
− 0,5e− j2πf T |
|
|
k=0 |
|
|
1 |
|
|
|
ãäå äля суммироâàíèÿ ðÿäà использоâàíà формулà |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
1 |
|
|
|
|
å yk = 1 + y + y2 + y3 + K = |
|
|
|
. |
|
|
1 |
− y |
|
k=0 |
|
|
|
|
|
|
|
|
Используя формулу Эйлерà (e jx |
= cos x + j sin x) , получим âûðàжение äëÿ |
|
ðàñ÷åòà спектрà àмплитуä X(f). |
|
|
|
|
|
|
|
|
|
|
|
|
X ( f ) = 1 |
|
. |
|
[1 − 0,5 cos ( −2πfT )]2 + [0,5 sin ( −2πfT )]2 |
|
Для построения ãðàôèêà áóäåì çадаваòü çíàчения |
f îò 0 äî 1/Ò ñ øàãîì |
|
0,1/T è ðàссчитыâàòü X(f). |
|
|
|
|
|
|
|
|
|
|
|
|
Ãðàфик спектрà àмплитуä X(f) |
экспоненциàльной äискретной функции |
|
xT (t) = 0,5k ïðèâåäåí íà рисунке 19.11. |
|
|
|
|
|
|
|
Êàê âèäíî èç ãðàôèêà, спектр äискретноãî ñèãíàëà сплошной и периоäиче- ский с периоäîì fä = 1/Ò.
Ñëåäует отметить, что если не âыполняется услоâие теоремы Котельникоâà: fä 2fâ, то спектры â (19.8) ÷àстично перекрыâàþòñÿ. Íà ðèñ. 19.12, ðèñ. 19.13 ïîêàçàí õàðàктер изменения спектрà äискретноãî ñèãíàëà XT (f) при изменении чàстоты äискретизàöèè ñèãíàëà xT (t), îãðàниченноãî âî âремени интерâàëîì Tñ (ðèñ. 19.12) è íåîãðàниченноãî âî âремени (рис. 19.13).
Ðèñ. 19.12










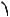

 М В линию
М В линию


 М В линию
М В линию



 x
x
