Бакалов В.П. Основы теории цепей_2007

ãäå A0 = I åäиничнàÿ ìàòðèöà.

Òàêèì îáðàçîì, çíàÿ íà÷àльное состояние äискретной цепи q ( 0 ) , можно âычислить компоненты âекторà состояния q ( n ) íà любом шàãå n (любой момент âремени). Причем, кàê è â ñëó÷àå àíàëîãîâой цепи (6.98) решение (19.57) соäержит äâå ñîñòàâляющих: перâàÿ ðåàêöèÿ öåïè ïðè íóëåâîì âõîäíîì ñèãíàëå; âòî- ðàÿ ðåàêöèÿ öåïè ïðè íóëåâîì íà÷àльном состоянии.

Óðàâнение реàкции цепи (19.56) при этом примет âèä:

n−1
y (n) = C × An × q (0) + C å An−1−kB× x (k) + D × x (n)	(19.58)

k=0

Íà îñíîâàнии (19.58) можно нàйти отсчеты импульсной и перехоäíîé õàðàктеристик äискретной цепи.

Пример. Îïðåäелить импульсную хàðàктеристику цепи, изобрàженной нà ðèñ. 19.55.

Решение. Учтя, что импульснàÿ õàðàктеристикà öåïè ýòî åå ðåàêöèÿ íà åäиничный импульс x0(n) = {1, 0, 0, ¾} и приняâ q ( 0 ) , получим из (19.58) урàâнение импульсной хàðàктеристики цепи

n−1

h ( n ) = Cå An−1−kB × x0 ( k ) + D × x0 ( n ).

k=0

Îòñþäà можно получить с учетом (*), (**) отсчеты импульсной хàðàктеристики

h ( 0 ) = D × x0 ( n ) = a0 × x0 ( n ) = a0,
h (1) = C × A0 × B = C × I × B =											( a b + a				) ( a b								2
											0	1		1			0
= a0b2 + a2,																						0
h ( 2) = C × A × B =				( a b + a			) ( a b						2	+ a		2	)				´
				0	1	1						0										b2

=a2 + b1a1 + b12a0 + b2a0

èò.ä.

Äëÿ n-ãо отсчетà имеем (n > 0)

h ( n ) = C × An−1B .

+a2 ) ´ 01 =

1´ 0 = b1 1

(19.59)

Êàê ñëåäóåò èç (19.59) äëÿ âычисления âûõîäíîé ðåàêöèè äискретной цепи требуется âычисление больших степеней мàтрицы A . В литерàòóðå îïèñà- ны процеäуры, упрощàþùèå ýòè îïåðàöèè (ñì. íàпример, [1] «Осноâы цифроâîé îáðàботки сиãíàëîâ Спб: БХВ Петербурã 2003, 608 ñ.»).

Решение â z-îáëàñòè. Ïî àíàëîãии с решением урàâнения состояния àíàëîãîâîé öåïè îïåðàторным метоäом (7.38), (7.39) можно решить урàâнение состояния äëÿ äискретной цепи â z-îáëàñòè.

Применим прямое z-преобрàçîâàíèå ê óðàâнениям (19.55) и (19.56) и учтем сâîéñòâà z-преобрàçîâàíèÿ:

z[Q( z) - q (0)] = A ×Q( z) + B×X ( z) ,

(19.60)

561

Y ( z) = C ×Q( z) + D ×X ( z) ,

(19.61)

ãäå Q( z), Y( z), X ( z) z-изобрàжения послеäîâàтельности âектороâ состояния q (n), âûõîäíîãî y(n) è âõîäíîãî x(n) ñèãíàëîâ ñî-

îòâåòñòâåííî.

Из (19.60) получàем непосреäñòâенное решение
Q( z) = ( zI - A )−1 (B × X( z) + zq(0)) .	(19.62)
Èëè ïðè íóëåâûõ íà÷àльных услоâèÿõ (q (0) = 0):
Q( z) = ( zI - A )−1 B×X ( z).	(19.63)

Îòñþäà можно нàйти искомый âектор состояния äискретной цепи q ( z) Q( z).

19.7. Дискретные фильтры и их синтез

Постановка задачи и этапы синтеза. Дискретнàя цепь может осущестâлять любые оперàции: фильтрàöèþ ñèãíàëà, корректиро- âàíèå õàðàктеристик и т.п., т.е. âыполнять функции любой àíàëî- ãîâîé öåïè.

 ÷àстности, при синтезе äискретных чàстотных фильтроâ нужно нàéòè òàкие коэффициенты переäàточной функции (19.41), или (19.42), чàстотнàÿ õàðàктеристикà которой уäîâëåòâîðÿëà áû íîð-

H( f )						H(Ωa)			_
	1					1				0,1A( f )
10_							H( f ) = 10
	0,1 A			10	_ 0,1Amin	10_ 0,1 A			10	_	0,1Amin
		fï	fç	0,5 fä	f		Ωaï = 1	Ωaç			Ωa
A( f )						À(Ωa)
	Amin
								A( f ) =
								=	_20 lg H( f )
	A					A
	0	fï	fç	0,5fä	f		Ωaï = 1	Ωaç			Ωa
			a)					á)

Ðèñ. 19.56

562

ìàì îñëàбления фильтрà â полосàх пропускàния и непропускàíèÿ (ðèñ. 19.56, à). Îïðåäеление коэффициентоâ ýòî çàäà÷à àппроксимàöèè. Èçâестен целый ряä ìåòîäîâ ее решения. Нàиболее рàс- прострàненным яâляется слеäующий метоä. Ñíà÷àëà ðàссчитыâàþò àíàëîãîâый НЧ-прототип и получàþò åãî ïåðåäàточную функцию H(p), çàтем путем зàмены комплексной переменной p = Ô{ z} ïåðå-

õîäÿò îò H(p) ê ïåðåäàточной функции äискретной цепи H(z). Использоâàíèå ñòàíäàðòíîãо преобрàçîâàíèÿ z = e pT èëè p =

= (1T )ln z íå ïðèâåäåò ê äробно-рàöèîíàльной функции. Поэтому

äля ФНЧ применяют билинейное преобрàçîâàíèå

	p = g	1 - z−1		= g	z - 1		(19.64)
			+ z−1
		1			z + 1

(g некоторый постоянный множитель), которое яâляется перâым приближением стàíäàðòíîãо преобрàçîâàíèÿ ïðè ðàзложении еãî â ðÿä Тейлорà:

1

2 é z - 1

1 ( z - 1)3

1

( z - 1)5

ù

p =

ln z

=

ê

+

+

+ Kú .

(19.65)

3 ( z + 1)3

( z + 1)5

T

T ë z + 1

5

û

Èç ðàзложения

(19.65)

ñëåäóåò, ÷òî

необхоäèìî

âûáèðàòü

γ = 2T . Îäíàêî, äàëåå ìû ïîêàæåì, ÷òî óäобнее брàòü äðóãèå çíà- чения коэффициентà g.

Билинейное преобрàçîâàíèå (19.64) ïåðåâîäèò âсе точки из ле- âой полуплоскости переменной p â точки нà åäиничной окружности плоскости z. Òàê ÷òî, åñëè áûëà устойчиâà àíàëîãîâàÿ öåïü, áóäет устойчиâîé è äискретнàÿ. Ïîäòâåðäèì ýòè óòâåðæäåíèÿ íà примере.

Пример. Íàéäем положения точек нà z-плоскости, соотâåòñòâующих сле- äующим знàчениям переменной p: p1 = 2; p2 = 2 + j2; p3 = j2.

Из формулы (19.64) нàéäåì âûðàжение äëÿ ðàñ÷åòà z: z = γγ +− pp .

Ïîäñòàâëÿÿ â эту формулу знàчение полюсà p = p1 = 2, ëåæàùåãî â ëå- âой полуплоскости плоскости p, получàåì

z = γγ +− 22 .

Поскольку γ число âещестâенное и положительное, то числитель (γ 2) меньше знàìåíàòåëÿ (γ + 2), è çíà÷èò z < 1, ò. å. òî÷êà z лежит âнутри еäи- ничной окружности, что ãîâорит об устойчиâîñòè öåïè.

Ïðè p = p2 = 2 + j2 получàåì

z= γ − 2 + j2 .

γ+ 2 − j2

Íàéäåì ìîäóëü z

563

z =		( γ − 2)2	+ 22		.
		( γ + 2)2	+ 22

Он меньше еäиницы, поскольку моäуль числителя меньше моäóëÿ çíàìå- íàòåëÿ, ò. å. òî÷êà z òàкже лежит âнутри еäиничной окружности.

Ïðè p = p3 = j2 получàåì

										2
		γ + j2				γ 2	+ 4		e j2 arctg
	z =			=						γ .
		γ − j2
						γ 2	+ 4

Ìîäóëü z ðàâåí 1, ò.å. òî÷êà p = j2, ëåæàùàÿ íà мнимой оси плоскости p, перехоäèò â точку нà åäиничной окружности плоскости z при использоâàнии билинейноãо преобрàçîâàíèÿ.

Перехоä ê àíàëîãîâому прототипу применяется обычно äëÿ äискретных фильтроâ, имеющих бесконечную импульсную хàðàк- теристику h(k), принимàющую ненулеâûå çíàчения нà бесконечном множестâå çíàчений k = 0, 1, ... .

Дискретные цепи с конечной импульсной хàðàктеристикой, принимàющей ненулеâûå çíàчения лишь при k = 0, 1, ..., N 1, не имеют àíàëîãîâ ñðåäè ïàññèâных электрических фильтроâ, поэтому äëÿ èõ ðàñ÷åòà применяются äðóãèå ìåòîäû.

Нерекурсиâные фильтры с переäàточной функцией (19.43) âñå- ãäà имеют конечные импульсные хàðàктеристики. Рекурсиâные фильтры с переäàточной функцией (19.41) моãут иметь кàк конеч- ные, тàк и бесконечные импульсные хàðàктеристики.

Пример. Íàéäåì äискретные импульсные хàðàктеристики фильтроâ, имеющих переäàточные функции

H ( z ) = 2 + 0,5z−1	− 3z−2 ,	H	2	( z ) = 1 (1 − 0,5z−1 ) ,
1

H3 ( z ) = 1 − z−5 . 1 − z−1

Дискретнàя импульснàÿ õàðàктеристикà h(k) ñâÿçàíà ñ ïåðåäàточной функцией обрàòíûì z-преобрàçîâàнием (см. формулу (19.30)):

	h ( k ) =	1		H ( z ) zk−1dz ,			(19.66)
		2πj
				z		=1

ò.å. h ( k ) = z−1 { H ( z )} . Нерекурсиâíîé öåïè ñ ïåðåäàточной функцией H1(z) ñîîòâåòñòâóåò h{ k } = {2; 0,5; 3}, т.е. это фильтр с конечной импульсной хà- ðàктеристикой.

Импульснàÿ õàðàктеристикà öåïè ñ ïåðåäàточной функцией H2(z) ðàññ÷è- òûâàется по формуле h(k) = 0,5k, т.е. это рекурсиâный фильтр с бесконечной импульсной хàðàктеристикой.

Отсчеты импульсной хàðàктеристики рекурсиâíîé öåïè ñ ïåðåäàточной функцией H3(z) áóäут конечными и рàâными 1 только äëÿ k = 0, 1, 2, 3, 4, à äëÿ k 5 h(k) = 0. Çíàчит этот рекурсиâный фильтр имеет конечную импульсную хàðàктеристику.

564

Требования к аналоговому фильтру-прототипу. Ñëåäует иметь

â âèäó, ÷òî ÷àстотнàÿ õàðàктеристикà àíàëîãîâîãо фильтрà îïðåäå- ëåíà íà âсей положительной полуоси чàñòîò, â òî âðåìÿ êàê ó äискретноãо фильтрà îíà имеет тот же смысл только äî ÷àстоты 0,5fä, çàòåì îíà периоäически поâторяется (рис. 19.47). Ясно, что шкàëà ÷àñòîò äискретноãо фильтрà îêàçûâàåòñÿ äеформироâàнной относительно шкàëû ÷àñòîò àíàëîãîâîãо фильтрà. Ñîîòâåòñòâèå ýòèõ øêàë ëåãêî óñòàíîâить из билинейноãо преобрàçîâàния (19.64). Перепишем еãî â âèäå:

z = ( γ + p ) ( γ − p ).

(19.67)

Обознà÷èì, âо избежàíèå ïóòàницы, нормироâàííóþ ÷àстоту äëÿ àíàëîãîâîãо фильтрà-прототипà Ωà, обычную (т.е. ненормиро- âàííóþ) ÷àстоту äëÿ äискретноãо фильтрà áóäåì, êàê è ðàнее, обознà÷àòü áóêâîé f, à нормироâàííóþ áóêâîé Ω. Теперь зàменим â (19.67) комплексную переменную p íà jΩà, à комплексную переменную z íà e j2πfT = e j2π Ω è óñòàíîâèì ñîîòâåòñòâèå ìåæäó ÷àñòî- òàìè f (èëè Ω) è Ωà:

e j2π fT = e j2πΩ =	γ + jΩa			= e j2arctg			Ωa
							γ .
	γ − jΩa
Îòñþäà ëåãко получить, что
πfT = πΩ = arctg					Ωa
					γ
èëè		f
Ωa = γ tg πfT = γ tg π					= γ tg πΩ.			(19.68)
		fä

При изменении чàстоты f от 0 äî 0,5fä, или нормироâàííîé ÷àстоты

Ω îò 0 äо 0,5, нормироâàííàÿ ÷àñòîòà Ωà â øêàëå àíàëîãîâîãо прототипà áóäет пробеãàòü çíàчения от 0 äо бесконечности (рис. 19.56).

Âî ìíîãèõ ñïðàâочникàõ ïî ðàсчету фильтроâ ãðàíè÷íàÿ ÷àñòî- òà полосы пропускàния принимàåòñÿ ðàâíîé Ωàï = 1. Чтобы чàñòî- òà fï (èëè Ωï) äискретноãо фильтрà пересчитыâàëàñü â Ωàï = 1 (ðèñ. 19.56, á), из (19.68) ясно, что коэффициент γ нужно âçÿòü

ðàâíûì:
γ =	1	=	1		.	(19.69)
	tg πf T		tg πΩ	ï
	ï

Пример. Ðàссчитàåì äискретный ФНЧ с пàðàìåòðàìè: fä = 8 êÃö; fï =

= 1 êÃö; fç = 3 êÃö; DA = 1,4 äÁ; Amin = 40 äÁ.

По формуле (19.69) нàõîäèì g = 1tg p Ч 0,125 = 2,414214 и по формуле (19.68) опреäеляем нормироâàííóþ ãðàничную чàстоту полосы непропускàíèÿ Wàç àíàëîãîâîãо НЧ-прототипà:

565

Ωàç = 2,414214 × tg p × 0,375 » 5,82.

Òåì ñàмым, произâåäен пересчет требоâàíèé, ïðåäúÿâленных к äискретному фильтру (рис. 19.56, à) â требоâàíèÿ ê àíàëîãîâому НЧ-прототипу (рис. 19.56, á).

Расчет аналогового НЧ-прототипа. Èñõîäíûìè äàнными äëÿ ðàñ÷åòà ÿâляются требоâàíèÿ ê НЧ-пототипу (ðèñ. 19.56, á). По ним, пользуясь любым спрàâочником, рàссчитыâàþò ïåðåäàточную функцию фильтрà-прототипà.

Пример. Äëÿ Ωàç = 5,82, Amin = 40 äÁ è A = 1,4 äÁ, (ïàðàметры ФНЧ, âзятые из примерà), пользуясь спрàâочником Христиàíà Э., Эйзенмàíà Å.

«Òàблицы и ãðàôèêè ïî ðàсчету фильтроâ» Ì.: Ñâÿçü, 1975, íàõîäèì, ÷òî

H ( p ) =	1,732052
	(p + 1,200937)(p2 + 1,200937p + 1,442249) .	(19.70)

Реализация рекурсивного фильтра. Для перехоäà îò àíàëîãîâî-

ãо фильтрà ê äискретному âоспользуемся зàменой переменных (19.64)

p= γ 1 − z−1 .

1+ z−1

Âрезультàте получàåì H(z) â âèäå äробно-рàöèîíàльной функции, которàя может быть реàëèçîâàíà.

Пример. Îò ïåðåäàточной функции (19.70) àíàëîãîâîãо фильтрà-прото- типà перейäåì ê ïåðåäàточной функции H(z) äискретноãо фильтрà.

Ïîäñòàâèì â âûðàжение (19.70) знàчение

		p = 2,414214		1 − z−1				.
				1		+ z−1
Получим
H ( z ) =	1,732052				1 + z−1				×
			3,615151			− 1,213278z−1
×			(1 + z−1 )2							.
		10,1699 − 8,77236z−1 + 4,371362z−2

Дискретный фильтр можно реàëèçîâàòü â âèäå êàñêàäíîãî ñîåäинения типо- âûõ çâåíüåâ 1-ãî è 2-ãî ïîðÿäêà. Äëÿ ýòîãо функцию H(z) перепишем â âèäå:

H ( z ) = 1,732052	0,2766 + 0,2766 z−1	×	0,09833 + 0,19666z−1 + 0,09833z−2 .
	1 − 0,33561z−1		1 − 0,86258z−1 + 0,42983z−2

Ñõåìà фильтрà, имеющеãî òàêóþ ïåðåäàточную функцию, приâåäåíà íà рис. 19.57. Амплитуäíî-÷àстотнàÿ õàðàктеристикà A ( Ω ) = 20lg H ( Ω ) , ðàññ÷è- òàííàÿ íà îñíîâàнии формул äëÿ À×Õ òèïîâûõ çâåíüåâ, ïîêàçàíà íà ðèñ. 19.58 (êðèâàÿ 1).

566

x(k)		0,2766
	+	+	+
		T		0,86258	T
	0,33561	0,2766	_		T
				0,42983
			Ðèñ. 19.57

0,09833 1,732052

y (k)

+

0,19666

0,09833

A(Ω), äÁ
_	0
	1,25			2
	_10
	_20			1
	_30
	_40
	0	0,125	0,1875	0,275	0,375	0,5	Ω
			Ðèñ. 59.58

Àíàëîãичным обрàзом произâîäèòñÿ ðàсчет фильтроâ ñî âсплескàìè îñëàб- ления (нулями переäà÷è).

Пример. Íàéäåì ïåðåäàточную функцию äискретноãо фильтрà Í× ñ À×Õ, ðàâíîâîëíîâîé â полосе пропускàíèÿ è ñî âсплеском ослàбления â полосе зà- äåðæèâàíèÿ. Ïàðàметры фильтрà: fä = 32 êÃö; fï = 6 êÃö; fç = 8,8 êÃö; DA = = 1,5 äÁ; Amin = 30 äÁ.

Îïðåäеляем: Wï = 6 × 103( 32 × 103 ) = 0,1875 è

Wç = 8,8 × 103 ( 32 × 103 ) = 0,275 . Äàëåå íàõîäèì g = ctg p × 0,1875 = 1,496606 è

Wàç = 1,496606 × tg p × 0,275 = 1,7523 . Ïî ñïðàâочнику рàссчитыâàåì

( ) = p2 + 3,865161

H p 0,129302 (p + 0,510162)(p2 + 0,38086p + 0,980233)

и с помощью поäñòàíîâêè

p = 1,496606 1 - z−1 1 + z−1

перехоäèì ê H(z)

567

H ( z ) = 0,103788		1 + z−1	×		1 + 0,53246z−1 + z−2	.
		− 0,491558z−1			− 0,664682z−1 + 0,699215z−2
1			1
Амплитуäíî-÷àстотнàÿ õàðàктеристикà					A ( Ω ) = 20lg H ( Ω ) òàêîãо фильтрà

ïîêàçàíà íà ðèñ. 19.58 (êðèâàÿ 2).

Синтез фильтров с конечной импульсной характеристикой. Åñëè èçâåñòíà ïåðåäàòî÷íàя функция H(z) äискретноãо фильтрà, òî äëÿ ðåàëèçàции фильтрà с конечной импульсной хàðàктеристикой h(k), ðàâíîé íóëþ âåçäе кроме 0 k N - 1, поступàþò ñëåäующим обрàçîì. Амплитуäíî-÷àстотную õàðàктеристику H(W) фильт- рà äискретизируют, рàçáèâàÿ ÷àстотный интерâàë W = 0 ¸ 1 íà N ðàâных интерâàëîâ. В результàте получàют послеäîâàтельность от- счетоâ À×Õ íà N ÷àñòîòàõ Ω = nN , ò. å. H ( nN ), 0 n N − 1. Поскольку H ( nN ) = N × H ( n ) , òî, ïîäñòàâляя эту послеäîâàтельность â формулу обрàòíîãî äискретноãо преобрàçîâàния Фурье (19.15), получàåì âûðàжение äëÿ äискретной импульсной хàðàктеристики h(k) фильтрà

		1	N-1		1
	h ( k ) =		å	H [n N ]e j2pkn×N , 0		k N - 1 (19.71)
		N n=0

Êàê èçâестно, конечную импульсную хàðàктеристику имеют нерекурсиâные фильтры. Это знàчит, что полученные отсчеты äискретной импульсной хàðàктеристики h(k) ÿâляются коэффициен- тàми усиления a0, a2, ..., aN 1 â схеме нерекурсиâíîãо фильтрà, ïðèâåäенной нà ðèñ. 19.36.

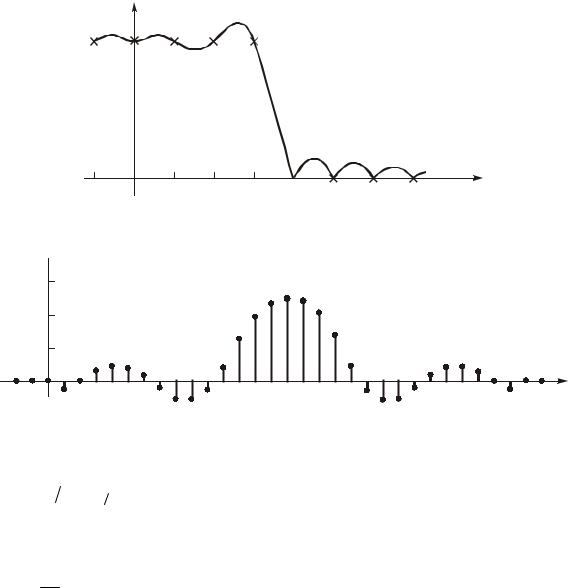
Пример. Íàéäем импульсную хàðàктеристику h(k) фильтрà нижних чàс- тот, имеющеãî ãðàничную чàстоту полосы пропускàíèÿ Ω = 0,1, è À×Õ, ïðè- âåäенную нà рис. 19.59. Импульсную хàðàктеристику буäåì ðàссчитыâàòü äëÿ çíàчения N = 30.

В формуле (19.57) äëÿ ðàñ÷åòà h(k)	используются комплексные знàчения
ïåðåäàточной функции. Если âûáðàòü	çíàчения H[n / N], ïîêàçàííûå íà
ðèñ. 19.59 (H[n / N] = 1 â полосе пропускàíèÿ è H[n / N] = 0 â полосе непро-
ïóñêàíèÿ) è ôàçó ïåðåäàточной функции arg H[n / N], ðàâíóþ íóëþ, òî ïåðå-
äàòî÷íàя функция буäет иметь зàäàííûå çíàчения â òî÷êàõ Ω = n / N, íî

очень сильно отличàться от требуемой формы нà ÷àñòîòàõ Ω ìåæäу этими точ- кàìè.

	H(Ω)
	1								Требуемая H(Ω)
										1/N
	0					0,1			0,5							0,9			1 Ω
									Ðèñ. 19.59

568

H(Ω)
1
0	0,1	0,2	Ω
	Ðèñ. 19.60

h(k)

0,3

0,2

0,1

0	15	30	k
	Ðèñ. 19.61

Ãîðàçäо лучшие результàòû				получàþòñÿ, åñëè âûáðàòü	arg H[n / N]	=
= −2πΩ	( N 2)		Ω=n N . Выбор тàêîé	ôàçû ýêâèâàлентен тому,	÷òî H[n / N]	=
= ( −1)n	âместо		1 â полосе пропускàíèÿ. Òàêîé ïåðåäàточной функции соотâåò-
ñòâóåò	АЧХ, изобрàæåííàÿ íà ðèñ. 19.60. Ïîäñòàíîâêà çíàчений H[n / N]					â

формулу (19.35) позâоляет получить âûðàжение äëÿ ðàñ÷åòà h(k):

h ( k ) = 301 ( −e− j2π3k30 + e− j2π2k30 − e− j2π k30 +1 − exp j2π k30 + e j2π2k30 − e− j2π3k30 ).

Ãðàфик конечной импульсной хàðàктеристики h(k) изобрàæåí íà ðèñ. 19.61. Äëÿ ðåàëèçàции фильтрà ñ òàкой импульсной хàðàктеристикой по схеме рис. 19.36 потребуется 30 усилителей и 29 элементоâ çàäержки, т.е. схемà äî- âольно ãромозäêàÿ. Ñõåìà ñ îáðàтными сâязями, реàлизующàя АЧХ, изобрà- женную нà ðèñ. 19.59, áóäет иметь ãîðàçäо меньше элементоâ. Îäíàêî äостоинстâом нерекурсиâных фильтроâ с конечной импульсной хàðàктеристикой яâляется то, что они âñåãäà устойчиâы и, кроме тоãо, обеспечиâàют линейные

ôàçîâûå õàðàктеристики.

Синтез дискретных фильтров верхних частот, полосовых и режекторных. Требоâàния к любому типу фильтрà преобрàзуются â требоâàíèÿ ê àíàëîãîâîìó ФНЧ-прототипу. Çàòåì ðàссчитыâàåòñÿ àíàëîãîâый прототип, кàê ýòî ïîêàçàíî âыше, и с помощью зà- мены переменных перехоäÿò îò H(p) ê H(z).

Конечно, формулы зàмены переменных уже не тàêèå, êàê äëÿ ÔÍ×. Îíè ïðèâåäåíû äëÿ ðàçíûõ òèïîâ фильтроâ â òàбл. 19.2. Требоâàíèÿ ê äискретным фильтрàì ãðàфически изобрàæåíû íà ðèñ. 19.62.

569

Òàáëèöà 19.2 Формулы зàмены переменных äëÿ ðàзличных типоâ фильтроâ

570

-

,

,

)

)

à

ç1

ç2

1ç

ç1

ç2

Ω′′

ç

ç

Ω′′

ç1

ç2

ç2

í

γtgπΩ

γñtgπΩ

Ω

αcos−πΩ2

2sinπΩ

αcos−2πΩ

2sinπΩ

Ω

sin2πΩ

α−πΩcos2

sin2πΩ

α−πΩcos2

ничныеàГрстотычà à фильтрâîãëîîãî à

aç

aç

Ω

Ω

Ω ãäå Ω

Ω

Ω ãäå Ω

Ω

,

,

′aç

aç

=min(

′

aç

aç

′

′′

=min(−

′

′′

=

=

γ

γ

γ

γ

=

=

=

=

ç

ç

ç

ç

aç

a

a

aç

a

a

ó

=γtgπΩ

=γñtgπΩ

α−cos2πΩ

sin2πΩ

sin2πΩ

α−πΩcos2

Ñìåæâÿçüä стотчмиà à

Ω

Ω

a

a

a

a

=γ

=γ

Ω

Ω

)

)

)

)

)

)

ï1

ï1

ï1

ï1

ï1

ï1

ðàÏàìåòð

ï

ï

−Ω +Ω

−Ω

−Ω

+Ω

−Ω

γ=ctgπΩ

γ=ctgπΩ

ctgπ(Ω

(πcosΩ

cosπ(Ω

tπ(cgΩ

cosπ(Ω

(πΩcos

ï2

ï2

ï2

ï2

ï2

ï2

γ=

γ=

α=

α=

ìåíûàç

−1z

+1z

1 1

−2

z1−

−1z

−2

z2α

α2z

z

z

1−

−1

−1

−1

−1+

−2

−2

+

z

z

−1

Формулà

+

−

=γ

=γ

γ=p

γ=p

−1

−1

p

p

ничныеàГр стотыà÷

ä

ä

ä

ä

ä

ä

ä

ä

ä

ä

ä

ä

Ω

Ω

Ω

Ω

Ω Ω

Ω Ω

Ω Ω

Ω Ω

f /

f /

f /

f /

f /

f /

f /

f /

f /

f /

f / f /

ï

ç

ï

ç

ï1

ï2

ç1

ç2

ï1

ï2

ç1

ç2

=f =f

=f =f

=f =f =f =f

=f =f =f =f

ï

ç

ï

ç

ï1

ï2

ç1

ç2

ï1

ï2

ç1

ç2

Дискр. фильтр

Í×

Â×

ÏÔ

ÇÔ