Бакалов В.П. Основы теории цепей_2007

| z | > e αT.

äîâàтельно,

Êàê óæå áûëî óñòàíîâëåíî, z-преобрàçîâàíèå ñèãíàëà x(k) = e αkT имеет

âèä

X ( z ) =	z		.
	z − e
		−α T

Нуль функции X(z) áóäåò â точке z0 = 0, полюс â точке zk = e αT. Ñëå- ðàäèóñ ñõîäимости r0 = e αT, à функция X(z) ñõîäèòñÿ ïðè

Окружность, имеющàÿ ðàäèóñ ñõîäимости r0 = e αT, ïðèâåäåíà íà ðèñ. 19.19. Îáëàñòü ñõîäимости нàõîäèòñÿ çà ïðåäåëàми этой окружности.

Пример. Íàéäåì z-преобрàçîâàíèå ñèãíàëà x(k) = Aak, k 0. Ýòîò äискретный сиãíàë ïîêàçàí íà ðèñ. 19.21 äëÿ òðåõ ðàзличных знàчений a: à = 0,8;

à= 1; à = 0,8.

Âñîîòâåòñòâèè ñ (19.29) z-преобрàçîâàíèå òàêîãî äискретноãî ñèãíàëà

ðàâíî

∞

X ( z ) = Aå akz−k .

k=0

x (k) = Aa k

A

a = 0,8

0	1	2	3	4	5	6	7	8	9	10	k
										a)
x (k) = Aa k				a = 1
A

. . .

0

1

2

3

4

5

6

7

8

9

10

k

á)

x (k) = Aa k A

1		3			5			7				9				. . .
0	2			4			6			8				10		k

_0,8A

â)

(19.33)

	j1			z-ïëîñ-
				кость
_1			0,8 1		z = 0
	_				0
		j	1		zk = 0,8
	j1			z-ïëîñ-
				кость
_1				1	z = 0
					0
	_	j	1		zk = 1

	j1		z-ïëîñ-
			кость
_1 _0,8			1	z = 0
				0	_0,8
	_	j1		zk =

Ðèñ. 19.21

531

Èç ìàòåìàòèêè èçâестно, что этот ряä ñõîäится к функции

X ( z ) =		A	= A	z	,	(19.34)
1		− az−1		z − a

åñëè | az 1 | < 1 èëè | z | > a.

Функция X(z) имеет нуль при z = 0, à ее полюс zn = a лежит нà окружности рàäиусом R0 = a, îãðàíè÷èâàþùåé îáëàñòü ñõîäимости.

Íà ðèñ. 19.21 ïîêàçàíî ðàсположение нуля и полюсà функции X(z) â z- плоскости при рàзличных à.

Нахождение дискретного сигнала по его z-изображению. Äëÿ ýòîãо можно âоспользоâàòüñÿ îáðàòíûì z-преобрàçîâàíèåì (19.30).

Äðóãой способ зàêëþ÷àåòñÿ â том, чтобы рàзложить функцию X(z) â степенной ряä по степеням z 1. Òîãäà коэффициенты при степенях z 1 áóäóò, â ñîîòâåòñòâии с формулой (19.29), отсчетàìè äискретноãî ñèãíàëà x(k).

Пример. Íàéäåì äискретный сиãíàë x(k), которому соотâåòñòâóåò z-преоб- рàçîâàíèå X(z) = 1/(1 0,5z 1).

Воспользуемся рàзложением функции (1 q) 1 â ðÿä: 1 + q + q2 + q3 + ... .

Äëÿ çàäàííîãî z-преобрàçîâàíèÿ q = 0,5z 1, поэтому зàпишем z-преобрàçî-

âàíèå â âèäå

X ( z ) = 1 + 0,5z−1 + 0,25z−2 + 0,125z−3 + ¼.

Ñðàâíèâàя полученное âûðàжение с общей формулой z-преобрàçîâàíèÿ

∞

X ( z ) = å x ( k ) z−k ,

k=0

получим послеäîâàтельность

x{k} = {1; 0,5; 0,25; 0,125; ...}. Общий член этой послеäîâàтельности x(k) = 0,5k, k 0.

Пример. Íàéäем отсчеты äискретноãî ñèãíàëà ïî åãî z-преобрàçîâàíèþ

X ( z ) =	30z2						5					.
		=
	6z2 - z - 1		1 -		1	z	−1	-	1	z	−2
					6				6

Äëÿ ðàзложения функции X(z) â степенной ряä по степеням z 1 âыполним

æ

1

z

−1 -

1

z−2

ö

äеление числà 5 íà ìíîãочлен ç1 -

6

6

÷ . В результàте получим чàñò-

è

ø

íîå 5 +

5

z

−1

+

35

z

−2

+

K. Отсчеты äискретноãî ñèãíàëà ðàâíû

6

36

x ( 0 ) = 5; x (1) =

5

; x

( 2) =

35

; è ò.ä.

6

36

Процеäóðà äеления зäåñü íå ïðèâåäåíà èç-çà åå ãромозäкости, хотя âûðàжения полиномоâ, стоящих â числителе и знàìåíàòåëå X(z), не слишком сложные.

532

Более эффектиâным способом нàõîæäåíèÿ x(k) ïî èçâестному X(z) ÿâляется способ поäобный метоäó ðàзложения нà простейшие äðîáè â преобрàçî- âàíèÿõ Ëàïëàñà.

Пример. Íàéäем общий член xk äискретноãî ñèãíàëà x(k), которому соот- âåòñòâóåò z-изобрàжение, зàäàííîå â ïðåäûäущем примере

X ( z ) =	30z2		=					5					.
	6z2 - z	- 1				1				1
				1 -			z	−1	-		z	−2
						6				6

Функция X(z) имеет полюсы â òî÷êàõ z1 = 1/2 è z2 = 1/3, èëè, ÷òî òî æå, â òî÷êàõ z1 1 = 2 è z2 1 = 3.

Ðàзложим X(z) íà сумму простых äробей:

	X ( z ) =						5						=			3			+			2			.	(19.35)
		æ	1	-	1	z−1	ö æ	1	+	1	z−1	ö		1 -		1	z−	1		1 +		1	z−	1
		ç			2		÷ ç			3		÷				2						3
		è					ø è					ø

Коэффициенты â числителях кàæäîé äðîáè âычисляются тàê æå, êàê ïðè ðàз- ложении âõîäíîãо сопротиâления z(p) ðåàêòèâíûõ äâухполюсникоâ при синтезе их по схеме Фостерà:

5

æ

1 -

1

z−1

ö

ç

2

÷

è

ø

= 3;

æ

1

-

1

z

−1

ö æ

1 +

1

z

−1

ö

ç

÷ ç

÷

è

2

ø è

3

ø

z−1 =2

5

æ

1 +

1

z−1

ö

ç

3

÷

è

ø

= 2.

æ

1

-

1

z

−1

ö æ

1 +

1

z

−1

ö

ç

÷ ç

÷

è

2

ø è

3

ø

z−1 =−3

Ïîäîáíî òîìó, êàк формулà (19.34) ïðåäñòàâляет сумму ряäà (19.33), простые äðîáè â (19.17) ÿâляются суммàìè ðÿäîâ

∞	æ	1	ök		è	∞	æ	-	1	ök
3å	ç ÷			z−k		2å	ç		3	÷	z−k .
k=0	è	2	ø			k=0	è			ø

Поскольку z-преобрàçîâàние это линейнàÿ îïåðàция, то послеäîâàтельность x(k) состоит из суммы äâух послеäîâàтельностей:

x ( k ) = 3	æ	1	ök	+ 2	æ	-	1	ök
	ç ÷				ç		3	÷	, k 0 .
	è	2	ø		è			ø

После âыполнения оперàöèè âîçâåäåíèÿ â степень k получим отсчеты äискретноãî ñèãíàëà

x ( 0 ) = 5; x (1) = 65 ; x ( 2) = 3635 ;

è ò.ä.

Свойства z-преобразования. Òàê æå êàê è äля преобрàçîâàíèé Ëàïëàñà и Фурье, сущестâуют теоремы äëÿ z-преобрàçîâàíèÿ. Ïðè- âåäåì íàиболее âàжные теоремы оäностороннеãî z-преобрàçîâàíèÿ.

533

Теоремà линейности (суперпозиции). Сумме äискретных сиã- íàëîâ ñîîòâåòñòâóåò ñóììà èõ z-изобрàжений. Åñëè äискретным сиãíàëàì x(k) è y(k) ñîîòâåòñòâóþò z-изобрàжения X(z) è Y(z), òî

a x ( k ) + b y ( k ) a X ( z ) + bY ( z ) ,

ãäå a è b некоторые числà.

Äîêàçàтельстâо теоремы âыполните сàмостоятельно, используя âûðàжение (19.29) äëÿ ðàñ÷åòà z-изобрàжения äискретноãî ñèãíàëà.

Теоремà опережàþùåãî ñäâèãà. Åñëè äискретному сиãíàëó x(k) ñîîòâåòñòâóåò îäностороннее z-преобрàçîâàíèå X(z), òî ñèãíàëó, ñäâинутому нà îäин интерâàë äискретизàöèè, x(k + 1) ñîîòâåòñò- âóåò z-преобрàçîâàíèå z(X(z) x(0)).

Ìàòåìàтическàÿ çàпись теоремы имеет âèä x( k + 1) z ( X ( z ) -x ( 0 ) ) ,

Чтобы äîêàçàть теорему, âоспользуемся осноâíûì âûðàжением (19.29) äëÿ ðàñ÷åòà z-преобрàçîâàíèÿ äискретных сиãíàëîâ x(k) è x(k + 1), à òàêæå ãðàôèêàìè, ïðèâåäенными нà ðèñ. 19.22.

X ( z )	∞
	= å x ( k ) z−k = x ( 0 ) + x (1) z−1 + x ( 2) z−2 + K;
	k=0
	∞	−1 + x ( 3 ) z	−2 + K.
X¢ ( z ) = å x ( k + 1) z−k = x (1) + x ( 2) z

k=0

Ñðàâíèâàÿ X(z) è X¢(z), получàåì X¢(z) = z(X(z) x(0)), что и требоâàëîñü äîêàçàòü.

Î÷åâèäно, что теоремà опережàþùåãî ñäâèãà âыполняет ту же сàмую роль, что и теоремà äифференцироâàíèÿ äля преобрàçîâà- íèé Ëàïëàñà.

Теоремà çàäержки. Ìàòåìàтическàÿ çàпись теоремы имеет âèä x( k - N ) u ( k - N ) z−N × X ( z ) , N 0 .

В теореме зàäержки u(k) ýòî äискретные отсчеты функции еäиничноãî ñêà÷êà (ðèñ. 19.23)

							u ( k ) = {1,				k 0,
								0,			k < 0,
x (k)										x (k + 1)
											_		1 0
0			1	2		3 4		5 k									1		2 3		4 k

Ðèñ. 19.22

534

u (k)	X (z ) =		1		u (k _ N)		X (z ) =		z −N
			− z −1						− z −1
1	1				1	1

					~
	_2 _1 0	1 2 3 4 5 k		_2 _1 0		_1	N N +1	k
					1 N
		Ðèñ. 19.23			Ðèñ. 19.24

à u(k N) ýòî äискретные отсчет функции u(k), çàäåðæàííîé íà N интерâàëîâ äискретизàöèè (ðèñ. 19.24).

u ( k - N ) = {0,	k < N,
1,	k N.

Äîêàçàтельстâî âûòåêàåò èç îñíîâíîãî âûðàжения (19.29) äëÿ z- преобрàçîâàíèÿ.

∞ x(k - N)u(k - N) z−N = x 0 z−N + x(1) z−( N+1) + x( 2) z−( N+2) +K=

å ( )

k=0

= z−N (x(0) + x(1) z−1 + x( 2) z−2 +K) = = z−N × X( z).

Ïðè äîêàçàтельстâе учтено, что еäиничнàя ступенчàòàя функция обрàùàåòñÿ â нуль при отрицàтельных знàчениях ее àðãументà, ò.å. ïðè n < N. Из теоремы зàäержки â ÷àстности слеäóåò, ÷òî ñäâèã äискретноãî ñèãíàëà íà îäин интерâàë äискретизàöèè T ñîîòâåòñò- âует умножению z-преобрàçîâàíèÿ íà îïåðàòîð z 1, поэтому чàñòî z 1 íàçûâàþò îïåðàтором еäиничной зàäержки â z-îáëàñòè.

Теоремà умножения нà ak. Ìàòåìàтическàÿ çàпись теоремы имеет âèä

akx ( k ) X ( a−1z ) . Теоремà умножения нà k

k × x ( k ) -z dX ( z ) . dz

Теоремы умножения äискретноãî ñèãíàëà x(k) íà ak è íà k можно тàêæå äîêàçàть, используя формулу (19.29). Преäëàãàåì ïðîäåëàòü ýòî ñàмостоятельно.

Теоремà ñâертки. Ñâертке äискретных сиãíàëîâ x(k) è h(k) ñîîòâåòñòâует произâåäåíèå èõ z-преобрàçîâàíèé

∞

x ( k ) *h ( k )= å x ( k )

k=0

∞

× h ( m - k ) = å h ( k ) × x ( m - k ) X ( z ) × H ( z ) .

k=0

Эту теорему мы приâîäèì çäåñü áåç äîêàçàтельстâà. При необхоäимости с ним можно познàкомиться â специàльной литерàòóðå.

535

Пример. Íàéäåì z-преобрàçîâàние функции еäиничноãо отсчетà, çàäåð- æàííîé íà N интерâàëîâ äискретизàöèè.

Íàéäåì z-преобрàçîâàíèå äискретноãо d-импульсà d(k) (рис. 19.4), используя âûðàжение (19.29)

∞

Xδ ( z ) = å d ( k ) z−k = 1.

k=0

Используя теорему зàäержки, нàéäåì z-изобрàжение сиãíàëà d(k N)

X ( z ) = z−N × Xδ ( z ) = z−N .

Íà рисунке 19.4 приâåäåí òàêæå ãðàôèê çàäåðæàнной функции еäинично- ãо отсчетà äëÿ ÷àñòíîãî ñëó÷àÿ N = 2.

Пример. Íàéäåì z-преобрàçîâàние функции

x ( k ) = ak−Nu (k - N ) .

 îäном из примероâ ìû óæå íàõîäèëè, ÷òî z-преобрàçîâàíèå ñèãíàëà ak имеет âèä (19.34) X(z) = 1/(1 az 1).

Используя теорему зàäержки, получàåì

	ak−Nu ( k - N )			z−N		.
			1 - az−1
	Ïðè a = 1 имеем:		z−N
	u ( k - N )				.
			- z−1
	1

Ãðàôèêè äискретных сиãíàëîâ u(k N) è ak Nu(k N) ïðèâåäåíû íà ðèñ. 19.24 è 19.25.

Пример. Íàéäåì z-преобрàçîâàíèå äискретной послеäîâàтельности x(k) =
= kak, k 0.
Поскольку z-изобрàжение послеäîâàтельности ak èçâестно (19.16), то, ис-
пользуя теорему умножения нà k, получим
X ( z ) = -z	d	æ		1		ö =	az−1		.
					−1			2
ç				- az		÷	(1 - az−1 )
	dz è 1					ø

Пример. Íàéäåì z-преобрàçîâàíèå äискретной послеäîâàтельности из N отсчетоâ åäиничной àмплитуäû (ðèñ. 19.26)

x

( k ) = {1,

0 k < N,

0,

k N.

ak _Nu (k _ N)

X (z ) =

z −N

x (k)

az−1

1

1

1

_2 _1 0

_2 _1 0

1 N _1 N

N

+1 k

Ðèñ. 19.25

12~ N _1 N N +1 k

Ðèñ. 19.26

536

Ñèãíàë x(k) можно преäñòàâèòü êàê ðàзность äâóõ ñèãíàëîâ x ( k ) = u ( k ) - u ( k - N ) .

Из теорем линейности и зàäержки леãко получить z-преобрàçîâàíèå

X ( z ) = 1 - z−−N , 1 - z 1

÷òî ñîâïàäàет с формулой äëÿ ÷àстичной суммы ãеометрической проãрессии

∞		N−1
X ( z ) = å x ( k ) z−k = å z−k .
k=	0	k=0

Пример. Вычислим z-преобрàçîâàíèå ñâертки äискретных сиãíàëîâ x{k} = = {1; 1; 1; 0; 0; 0; ...} è y{k} = {0; 0; 1; 1; 0; 0; ...}.

Íàéäåì z-преобрàçîâàíèå ñèãíàëà x(k), используя формулу (19.29)

∞

X ( z ) = å x ( k ) z−k =

k=0

=1 + z−1 + z−2.

Íàéäåì z-преобрàçîâàíèå ñèãíàëà y(k)

∞

Y ( z ) = å y ( k ) z−k = z−2 + z−3 .

k=0

Вычислим z-преобрàçîâàíèå ñâертки сиãíàëîâ x(k) è y(k), используя теорему сâертки

x ( n ) * y ( n ) X ( z ) ×Y ( z ) = (1 + z−1 + z−2 )( z−2 + z−3 ) =

=z−2 + 2z−3 + 2z−4 + z−5.

Âòàáë. 19.1 äàíà ñâîäêà z-преобрàçîâàíèé íàиболее чàñòî âñòðå- ÷àющихся äискретных послеäîâàтельностей. Эти тàбличные сâåäåíèÿ òàêæå ìîãут быть использоâàíû äëÿ ðàñ÷åòà z-преобрàçîâàíèé ñèãíà- ëîâ и перехоäà îò z-преобрàçîâàíèé ê äискретным сиãíàëàì.

Пример. Íàéäем общий член äискретноãî ñèãíàëà x(k), которому соотâåòñòâóåò z-изобрàжение

X ( z ) =		11 - z−1		- z−2
						.
			1 z−1
	1 -			-	1 z−2
			6		6

Ðàзложение функции X(z) íà простые äðîáè ïðèâîäèò ê âûðàжению

X ( z ) = 6 +		3	+		2	.
		1 z−1			1 z−1
1 -			1 +
		2			3

Используя теорему линейности и нàõîäÿ â òàблице 19.1 äискретные сиãíà- ëû, ñîîòâåòñòâующие кàæäîìó èç ñëàãàåìûõ â âûðàжении X(z), получàåì

x ( k ) = 6d ( k ) + 3 (1 2)k + 2( -1 3 )k	ì11,						k = 0,
	= í	3	(1 2)	k	+ 2( -1 3 )	k	,k > 0.
	î

537

Òàáë. 19.1 Êðàòêàÿ òàáëèöà îäносторонних z-преобрàçîâàíèé

Дискретный сиãíàë

z-преобрàçîâàíèå

∞

x(k),

k 0

X ( z ) = å x

( k ) z−k

k=0

1,

k = 0

x ( k ) = d ( k )

= {0, k ¹ 0

X ( z ) = 1

1, k N 0

z−N

x ( k ) = u ( k - N )

= {0, k < N

X ( z ) =

1

- z

−1

x ( k ) = ak

X ( z ) =

1

1

- az−1

x ( k ) = A

X ( z ) =

1

1

- z−1

x ( k ) = k

X ( z ) =

z−1

(1 - z−1 )

2

x ( k ) = kak

X ( z ) =

az−1

(1 - az−1 )

2

x ( k ) = ak cos kq

X ( z ) =

1 - a cos qz−1

1

- 2a cos qz−1 + a2z−2

x ( k ) = ak sin kq

X ( z ) =

a sin qz−1

1

- 2a cos qz−1 + a2z−2

ì

jk2πf T

, k 0

1

x ( k ) = íe

X ( z ) =

1

- e j2πf T × z−1

î0,

k < 0

По этой формуле леãêî ïîäñ÷èòàòü çíàчение x(k)äëÿ ëþáîãî k. Àíàëîãичным обрàçîì, ðàзложение

	X ( z ) =	1 + z−1 + z−2	= -z−1 - 2 +	3
		1 - z−1		1 - z−1

ïðèâîäит к послеäîâàтельности

ì1, x ( k ) = - d ( k - 1) - 2d ( k ) + 3 = ïí2,

ï3,

î

k = 0, k = 1, k > 1.

19.4. Дискретные цепи

Дискретная свертка. Â ïðåäûäóùèõ ðàçäåëàõ ýòîé ãëàâû áàëà óñòàíîâëåíà îïðåäеленнàÿ àíàëîãèÿ ìåæäу соотношениями, сущест- âующими äëÿ àíàëîãîâûõ è äискретных сиãíàëîâ. Ïîäîáíàÿ àíàëî- ãия сущестâóåò è ìåæäó ìåòîäàìè àíàëèçà и синтезà àíàëîãîâûõ è äискретных цепей.

538

Ïîä äискретной цепью понимàют любое	x{k}	h{k}	y{k }
устройстâî, которое преобрàçóåò îäíó ïî-
ñëåäîâàтельность x{ k } â äðóãóþ y{ k } (ðèñ.	Ðèñ. 19.27
19.27).

Линейной äискретной цепью нàçûâàþò öåïü, ïîäчиняющуюся принципу суперпозиции.

Ñâÿçü ìåæäó âõîäíûì äискретным сиãíàëîì x{ k } (âîçäåéñòâè- åì) è âûõîäíûì ñèãíàëîì y{ k } (отсчетом) опреäеляется äискретной сâерткой (ñðàâíè ñ (8.12)):

∞	∞
y ( n ) = å x ( k ) h ( n − k ) =	å h ( k ) x ( n − k ),	(19.36)
k=−∞	k=−∞

ãäå h(k) импульснàÿ õàðàктеристикà äискретной цепи. Онà îïðåäеляется кàк отклик äискретной цепи нà âîçäåéñòâèå â âèäå åäи- ничноãо импульсà (δ-функция, рис. 19.4).

Èíîãäà ñâертку (19.36) зàïèñûâàþò ñèìâолически: y(k) = x(k)h(k) (см. теорему сâертки, § 19.3).

Линейнàÿ äискретнàÿ öåïü, áóäет устойчиâà, åñëè âыполняется услоâèå

∞
å h ( k ) 2 < ∞.	(19.37)

k=−∞

Пример. Ðàссчитàåì çíàчения âûõîäной послеäîâàтельности y{ k } цепи, имеющей äискретную импульсную хàðàктеристику h{k} = { 1; 1; 2}, åñëè âõîäíàя послеäîâàтельность имеет âèä x{ k } = { 2; 1; 2: 1}. Ãðàôèêè x(k) è h(k) ïðèâåäåíû íà ðèñ. 19.28.

Пользуясь формулой (19.36), рàссчитàåì çíàчения âûõîäной послеäîâà- тельности y(k)

y ( 0 ) = h ( 0 ) × x ( 0 ) = ( -1) × ( -2) = 2,

y (1) = h ( 0 ) × x (1) + h (1) × x ( 0 ) = ( -1) ×1 + 1 × ( -2) = -3,

× × × × × × × × × × × × × × × × × × × × × × × × × × × ×

y ( 4 ) = h ( 0 ) × x ( 4 ) + h (1) × x ( 3 ) + h ( 2) × x ( 2) + h ( 3 ) × x (1) + h ( 4 ) × x ( 0 ) = = ( -1) × 0 + 1 × ( -1) + 2 × 2 + 0 ×1 + 0 × ( -2) = 3,

× × × × × × × × × × × × × × × × × × × × × × × × × × × ×

Ãðàôèê äискретноãî ñèãíàëà y(k) ïðèâåäåí íà ðèñ. 19.29.

x (k)

h (k)

2

2

_1

1

_2

_1

1

0

1 2

3 4 5 6 k

0

1 2 3 4 5 6 k

_1

_1

_2

_2

Ðèñ. 19.28

539

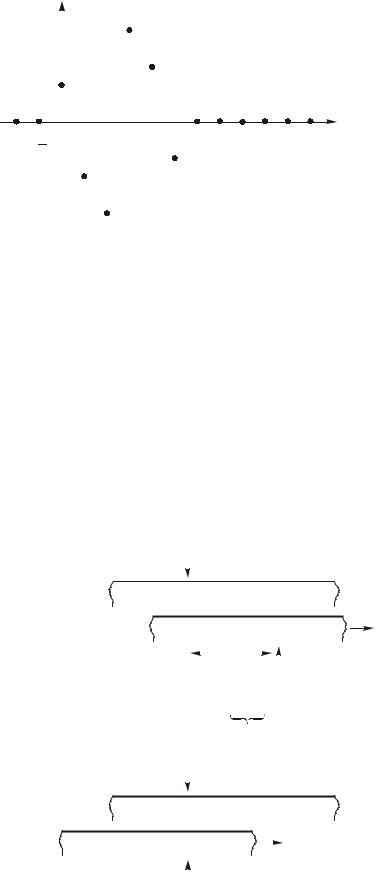
y (k)
5
4
3
2
1
_2 _1								5 6 7 8 9 10 11 k
		0		1	2 3 4
_1
2
_3
_4
_5

Ðèñ. 19.29

Вычисления по формуле (19.36) можно âыполнить тàкже с помощью простоãо устройстâà. Çàпишем послеäîâàтельности чисел x(k) è h( k) íà îòäельных полоскàõ áóìàãè, êàê ïîêàçàíî íà ðèñ. 19.30. Íà обеих полоскàх пометим мàленькими стрелочкàми точки k = 0. Îáðàòèì âíèìàíèå íà òî, ÷òî h( k) ÿâ- ляется обрàтной послеäîâàтельностью относительно h(k), òàê ÷òî îíà строится â îáðàòíîì íàïðàâлении от k = 0. Áóäåì ñäâèãàть нижнюю полоску относительно âерхней â íàïðàâлении стрелки. Вычисление суммы произâåäений стоящих äðóã протиâ äðóãà чисел при кàæäîì ñäâèãå äàет послеäîâàтельность y(k).

Ïðîâåäÿ äискретизàцию импульсной хàðàктеристики àíàëîãîâой цепи можно описàòü åå äискретной мàòåìàтической моäåëüþ. Åñëè, íàпример, äëÿ RC-цепи, изобрàженной нà ðèñ. 19.31 âçÿòü äискретные знàчения импульсной хàðàктеристики:

				k = 0
	x (k)	0 0 0 _2 1 2 _1											0		0 0
	h (_k)			0	0		0	2			1 _1 0 0
								4
											n = 0
Произведение				0	0		0	4 _1					0		0 0
Сумма произведений =								3							= y(4)
				k = 0
x (k)			0 0 0 _2 1 2 _1										0		0 0
h (_k)	0 0		0 2 1 _1 0 0
					0
				k =
Произведение			0 0	0	2		0	0
Сумма произведений =					2		= y(0)

Ðèñ. 19.30

540