3. Полуустойчивый предельный цикл. С одной стороны к нему стремятся соседние фазовые траектории, с другой стороны сходят. Возможны два варианта: полуустойчивый предельный цикл в сторону устойчивости(рис. 2.10, а), когда движение всегда устойчиво, так как при любых рассогласованиях система придет в особую точку– начало координат и полуустойчивый предельный цикл в сторону неустойчивости(рис. 2.10, б), движение всегда неустойчиво, так как при любых начальных отклонениях процессы расходятся.

a	x&	б	x&

0	0
x	x

Рис. 2.10. Полуустойчивый предельный цикл:

а – в сторону устойчивости, б – в сторону неустойчивости

2.2. Методы построения фазовых портретов

При построении фазовых портретов используют методы решения уравнений по участкам, изоклин, Льенара, d-метод.

Метод решения уравнений по участкам. Поясним этот метод на примере.

Пусть НСАУ имеет структуру, приведенную на рис. 2.11.

v = 0

Рис. 2.11

Дифференциальное уравнение

системы Tx&&+ x& + F (x)K = 0. Обозначим

x = -y; x& = -y& . Тогда T

dy&

+ y& = KF (x)

или

dt

dy&

ìb, x > a, y < a,

ï

T

+ y& = K í0,

x

< a,

y

< a,

(2.5)

dt

ï-b,

x

< -a, y > a.

î

Рассмотрим

участок,

соответствующий

зоне нечувствительности,

где

F (x) = 0 . Из (2.5)

T

dy&

+ y& = 0. Так как

dy

= y& ,

то dt =

dy

и T

dy&

y& = -y&

или

y&

dt

dt

dy

dy& = - 1 dy , откуда

T

85

y& = -

1

y + C .

(2.6)

T

0

На

участке, где F(x) = -Kb (x < -a; y > a),

дифференциальное

уравнение

T

dy&

+ y& = -Kb. После подстановки dt =

dy

получим T

dy&

y& = - y& - Kb,

откуда

dt

dyy&&

y&

dy

dy = -T

. Возьмем интеграл от обеих частей последнего равенства и пре-

y& + Kb

dy&( y& + Kb - Kb)

образуем правую часть: òdy = -T ò

+ C1, откуда

y& + Kb

y = T é

-dy& +

Kb

dy&

ù

+ C .

ú

ê

ò

ò y& + Kb

1

ë

û

Окончательно

y = T éKb ln ( y& + Kb) - y&

ù + C .

(2.7)

ë

û

1

Участок, где F (x) = Kb , исследуется аналогично. Получаются уравнения, симметричные рассмотренным.

Фазовый портрет, построенный по полученным выражениям, имеет вид,

приведенный			на	рис. 2.12, а			примерная кривая		процесса y(t) соответствует
рис. 2.13.
	-a		y&	a
	M5
				M			y(t)	M1
M 4				g		0
				M 6		y
				g	M1		M 0
	M3							M 2		M 6
							+a
										t
							0
				M 2			-a	M3	M	M5
										4
Рис. 2.12. Фазовый портрет НСАУ								Рис.2.13. Кривая процесса НСАУ

Метод изоклин. Пусть dy& = f1 (y, y&) = N , где N – наклон фазовой траекто- dy f2 (y, y&)

рии на плоскости (y&, y) .

Если на фазовой плоскости выбрать точки, которым соответствует один и

тот же наклон Ni	=	f1	(yi , y&i )	, то соединив их, можно получить линию, называ-
		f2
			(yi , y&i )

емую изоклиной (изоклина – это геометрическое место точек на фазовой плоскости, соответствующих одному постоянному значению наклона интегральных

86

кривых), а множество линий для разных значенийN –			семейство изоклин
(штриховые линии на рис. 2.14). Уравнение изоклин
y&i = f (Ni , yi ) .			(2.8)
Построение фазовой траектории		y& N
осуществляется так (рис. 2.14): строят		1	N2
изоклины; далее из начальной точки
		M 0	N3
M0 проводят два луча с наклонамиN1
и N2 до пересечения со следующей		M1
изоклиной; отрезок, отсекаемый ими
на следующей изоклине делят попо-
лам, точка M1 будет исходной точкой	0		y
для следующего построения.

Рис. 2.14. Построение фазовой траектории

Таким образом, фазовая траектория – это линия, проходящая через средние точки. Точность построения тем выше, чем больше изоклин.

Проиллюстрируем эту методику построением фазового портрета для системы из предыдущего примера.

Для участка

F (x) = 0 T

dy&

+ y& = 0;

dt =

dy

; T

dyy&&

+ y& = 0, откуда урав-

dt

dy&

1

y&

dy

нение изоклин

= -

= N (tga = N ) (рис. 2.15,

y

< a ).

dy

T

-a

y&

a

M5

M

M 4

M 6

g

0 y

gM1

M3

M 2

Рис. 2.15. Построение фазового портрета методом изоклин

Для участка F (x) = -Kb	dy&	= -	Kb + y&	= N, откуда y& = -	Kb	. Анало-
	dy				1 + NT
			Ty&

гично получается уравнение изоклин и для последнего участка. Сравнение рис. 2.12 и рис. 2.15 показывает, что результаты совпали.

Достоинством метода изоклин является возможность построения фазовых траекторий для любых начальных условий, а недостатками – трудоемкость процесса построения и отсутствие возможности исследования системы при изменении параметров во времени или в зависимости от изменения внешних воздействий.

87

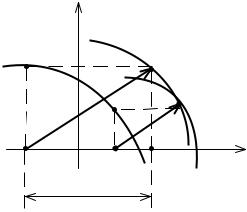
Метод Льенара. Этот метод применяется в том случае, когда свободное движение описывается уравнением вида:

&x& + f (x&) + x = 0 .

(2.9)

Наклон на фазовой плоскости определяется как

dx&	= -	f (x&) + x	.	(2.10)
dx
		x&

Льенар предложил на фазовой плоскости строить кривую x = - f (x&) , а затем определять направление движения траектории согласно следующему алгоритму:

1.	Выбирается начальная точка P	(x& , x )		и осуществляется движение из
	1	1	1
этой точки до пересечения с кривой x = - f (x&) .
2.	Из точки пересечения опускается перпендикуляр на ось x и находится
точка Q1 .
3.	Радиусом R , равным длине отрезка [ P ,				Q ], проводится дуга окруж-
	1			1	1
ности с центром в точке Q1 .
4.	На этой дуге произвольно выбирается точка P2 и процесс повторяется:
осуществляется движение до пересечения			с	кривойx = - f (x&) , определяется

Q2 , радиус R2 и т.д.

Для увеличения точности построения фазовых траекторий дуги окружности рекомендуется выбирать минимальной длины.

x&

x = - f (x&)	x&1	P
		1
		P2
Q1	Q2	x
		1

x

x + f (x&)

Рис. 2.16. Построение фазового портрета методом Льенара

К методу Льенара близок d-метод построения фазовых портретов, который также основан на построении окружностей, отрезки дуг которых составляют фрагменты фазовых траекторий, В отличие от метода Льенараd-метод позволяет исследовать процессы в системах с изменяющимися во времени коэффициентами, а так же вынужденные движения.

88