Исаченко Сопротивление материалов ч.1 2010

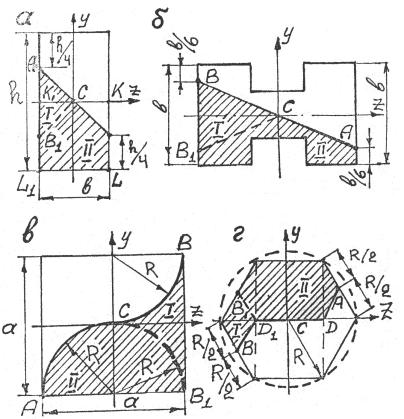
осям симметрии; при этом при повороте полуфигуры на 180° вокруг центра тяжести всей фигуры она (полуфигура) совпадает со второй полуфигурой (рис. 3.11).

Рис. 3.11

3.1.15. Главные центральные оси фигур типа рис. 3.11 являются главными осями их полуфигур.

Этот вывод будет очевиден, если провести дополнительную линию B1C (пунктир на рис. 3.11, а, б, в), симметричную ВС, дополнительную линию B1D1 (пунктир на рис. 3.11, г), симметричную

101

BD1 . У полученных частей I и II полуфигуры ось z для I части и ось

y для II части являются осями симметрии и, следовательно, для всей полуфигуры — главными осями.

3.1.16. Моменты инерции полуфигуры относительно осей, являющихся главными центральными осями всей фигуры типа рис. 3.11, равны половине величины моментов инерции относительно соответствующих главных центральных осей всей фигуры.

Этот вывод получим из рассмотрения, например, прямоугольника на рис. 3.11, а:

Iz (полуфигуры ACBLL1A) =

	=	1		bh3	+ Iz′(части ACK1) − Iz′′(части BCK ) =	1		bh3
									,
		2		12		2		12

так как Iz′ = Iz′′ .

Итак, для полуфигуры рис. 3.11, а Iz =

1

bh3

I y =

1

hb3

,

; для

2

12

2

12

полуфигуры

рис.

3.11,

в

Iz = I y =

1

a4

; для

полуфигуры

2

12

рис. 3.11, г Iz = I y

=

1

5 3

a4 .

16

3.1.17. Если

2

в)

фигура

имеет

две (см.

рис. 3.11,

и

более (см.

рис. 3.11, г) пары взаимно перпендикулярных осей симметрии, то любые две взаимно перпендикулярные оси, проходящие через центр тяжести всей фигуры, являются главными осями полуфигуры.

3.1.18. Сечения, имеющие более двух осей симметрии, т.е. все правильные многоугольники, начиная с равностороннего треугольника и заканчивая, в пределе, кругом, имеют бесконечное множество главных центральных осей инерции, относительно которых моменты инерции равны между собой.

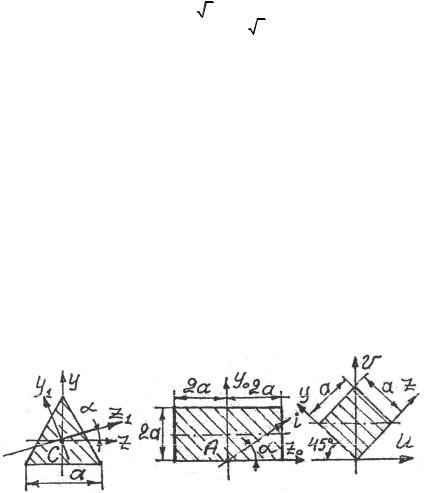
Действительно, для равностороннего треугольника (рис. 3.12) моменты инерции относительно осей z, y равны

						3	3
		3		a a
	bh					2			3		4
Iz =			=					=		a		.
	36				36				96

102

	a			3				3
	h					2a			a3		3
								2
I y = 2	2				=					=		a	4	, Izy = 0 .
	12							12			96
					8

Тогда для осей, проходящих под углом α ( α + 90 ) к осям z, y, согласно формуле (3.15) Iz1y1 = 0 , т.е. оси z1 , y1 – главные; согласно

формуле(3.14) Iz1 = I y1 = Iz = I y , т.е. ихзначениенезависитотуглаα.

3.1.19. Если моменты инерции относительно главных осей, проходящих через любую точку сечения (например, точку А сечения на рис. 3.13), равны, то все оси, проходящие через эту точку, являются главными осями и моменты инерции относительно их равны.

С учетом того, что

					Iz		=	4a(2a)3	=	32	a	4	и	I y	=	2a(4a)3		=		32	a	4	,
						0		3		3						12			3
а Iz														0
	0	y	= 0 ( y0					– ось симметрии), по формуле (3.14) получим, что
		0
независимо							от	угла α для					осей,	проходящих					через				точку А,
Ii =	32		a	4	.
		3

Рис. 3.12

Рис. 3.13

Рис. 3.14

3.1.20. Если относительно двух произвольных взаимно перпендикулярных осей, проходящих через данную точку сечения, моменты инерции равны, то главные оси проходят через эту точку сечения под углом в 45° к исходным осям (рис. 3.14).

103

Вывод следует из анализа формулы (3.16). При Iz = I y

2α0 = 90° , а α0 = 45°.

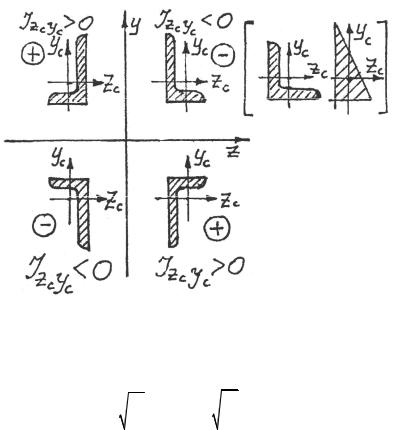
Для определения знака центробежного момента инерции Izc yc

для уголков равнобоких и неравнобоких, прямоугольных треугольников относительно центральных осей, параллельных полкам (катетам), которые не являются главными осями, удобно пользоваться схемой, представленной на рис. 3.15, согласно которой знак Izc yc ,

обратный знаку тангенса угла для каждого квадранта.

Рис. 3.15

К геометрическим характеристикам плоских фигур относятся также неинтегральные характеристики:

радиус инерции сечения относительно центральных осей

	iz =	I	z	> 0 ,	iy =	I y	> 0	, [м];	(3.20)
		F				F

осевые моменты сопротивления сечения относительно главных центральных осей

104

W					Iz	3
	z	=						> 0 , [м ],	(3.21)
					ymax

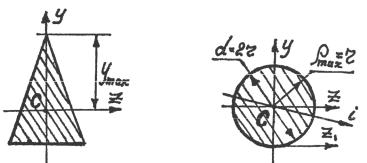
где ymax – ордината наиболее удаленных от оси z точек сечения

(рис. 3.16);

полярный момент сопротивления круглого сечения

	Wp =	I p	3
			> 0 , [м ],	(3.22)
		ρmax

где ρmax = r – расстояние до наиболее удаленной точки от центра круглого сечения (рис. 3.17).

Рис. 3.16

Рис. 3.17

Если геометрическая характеристика есть величина переменная, например, зависящая от угла поворота α, то ее экстремальные значения найдем, есливозьмемпроизводнуюпоα иисследуемнаэкстремум.

Приведем значения моментов инерции для простейших фигур, часто встречающихся в задачах.

Для квадрата со стороной а (рис. 3.18)

Iz = I y	= Ii				=		a4		,	(3.23)
							12
Iz = I y						a4
			=					,		(3.24)
					3
1	1
		7
Iu =				a4 .						(3.25)
	12

105

Для прямоугольника размерами b × h (рис. 3.19)

	Iz =			bh3		I y		hb3
					,		=			,		(3.26)
				12				12
	Iz			bh3		I y			hb3
		=			,		=				.	(3.27)
				3
	1					1		3

Для прямоугольного треугольника с катетами b, h (рис. 3.20)

Iz =			bh3					I y				hb3
						,			=						,		(3.28)
				36								36
Iz			bh3					I y						hb3
	=					,			=							,	(3.29)
1		12						1				12
							bh3
				Iz2		=				,							(3.30)
								4
		Izy = −					b2h2					,					(3.31)
								72
		Iz y				=	b2h2					,					(3.32)
								24
					1 1
	Iz				y	= −		b2h2					.				(3.33)
				2				8
					1

Рис. 3.18

Рис. 3.19

Рис. 3.20

106

Для круга радиусом r (см. рис. 3.17)

Iz = I y = Ii =			πr		4	πd 4	(3.34)
			4		=	,
						64
I p =	πr4		=	πd 4		,	(3.35)
	2				32
Iz	= 5		πr4 .				(3.36)
1		4

3.1.21. Учитывая свойство аддитивности геометрических характеристик, во многих задачах при их определении удобно достроить заданное сечение до такой простой фигуры, для которой геометрические характеристики известны.

3.2. Задачи

Задача 3.1. Для фигуры (рис. 3.21), ограниченной осью абсцисс и параболой y = azn , определить площадь, статический момент площади относительно оси y и положение центра тяжести – абсциссу zc .

Рис. 3.21	Рис. 3.22
Задача 3.2. Определить величину	размера h для фигуры

(рис. 3.22), при котором центр тяжести ее будет находиться на прямой AB.

107

Рис. 3.23

Рис. 3.24

Задача 3.3. Чему равен размер а, если главные центральные моменты инерции сечения (рис. 3.23) равны между собой? При полученном значении а записать выражение для определения главных центральных моментов инерции.

Задача 3.4. Определить моменты инерции относительно осей z и y для плоских фигур (рис. 3.24).

Задача 3.5. Для треугольника ADC (рис. 3.25) определить осевой момент инерции относительно медианы ОС, если h, b, α заданы.

Рис. 3.25

Задача 3.6. Определить момент инерции относительно оси z для фигуры, изображенной на рис. 3.26.

Задача 3.7. Найти момент инерции относительно оси z круга, имеющего n одинаковых вырезов, равномерно расположенных по окружности (рис. 3.27), если R1 = 0,5R ; R2 = 0,75R .

108

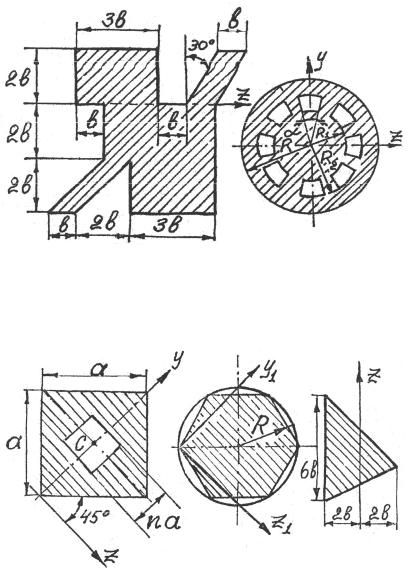
Рис. 3.26

Рис. 3.27

Задача 3.8. Сторона квадрата выреза равна na (рис. 3.28). Чему равно n, если Iz / I y = 5 .

Рис. 3.28

Рис. 3.29

Рис. 3.30

109

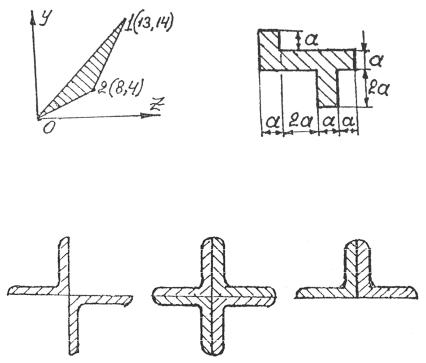
Задача 3.9. В окружность радиуса R вписан правильный шестиугольник (рис. 3.29). Определить центробежный момент инерции площади шестиугольника относительно осей z1 , y1 .

Задача 3.10. Для сечения (рис. 3.30) вычислить момент инерции относительно оси z.

Задача 3.11. Координаты вершин треугольника (рис. 3.31) приведены в сантиметрах. Определить момент инерции относительно оси y.

Рис. 3.31

Рис. 3.32

Задача 3.12. Для заданной плоской фигуры (рис. 3.32) показать положение главных центральных осей инерции.

Рис. 3.33

Задача 3.13. Сечения (рис. 3.33) составлены из уголков № 3 (30×30×3) по ГОСТ 8509-86. Показать, как будут проходить глав-

ные центральные оси сечений, и определить Iu = Imax , Iv = Imin . Задача 3.14. Определить момент инерции фигуры относительно

оси z (рис. 3.34).

110