Исаченко Сопротивление материалов ч.1 2010

α = α4 > 0 , α = α5 < 0 . При отсчете угла от направления σy нужно записать формулу (2.6) в виде:

	σn =	σy +σx	+	σy −σx	cos 2α −τyx sin 2α ,	(2.6а)
		2		2

где для определения σm угол α = α6 = (σy , m)> 0 , а для опреде-

ления σn угол α = α7 = (σy , n)< 0 .

Обращаем особое внимание на индексы у τyx в формуле (2.6а). Сумма σn + σm = σx + σy = II = const для плоского напряженно-

го состояния.

Касательное напряжение на наклонной площадке определяется с учетом всех указаний к формуле (2.6) по формуле:

	τnm =	σx −σy	sin 2α+ τxy cos 2α ,	(2.7)
		2

где α = α1 = (σx , n) > 0 .

Если исходные площадки – главные, то последний член в формулах (2.6), (2.7) обращается в нуль, так как τ на главных площадках равно нулю.

Формулы (2.6), (2.7) могут быть использованы и при исходном объемном напряженном состоянии, если одна из площадок – главная, так как на площадках, параллельных главному напряжению (перпендикулярных к главной площадке), последнее не вызывает никаких напряжений, ни нормальных, ни касательных (при растя- жении-сжатии продольные волокна не надавливают друг на друга и не сдвигаются друг относительно друга).

Для любого напряженного состояния

	τmax =	σmax −σmin	,	(2.8)
		2

где σmax и σmin – наибольшее и наименьшее по алгебраической величине исходные главные напряжения. τmax действует на площадке, расположенной под углом 45° к направлению σmax и σmin .

71

Для плоского напряженного состояния для определения τmax можно, кроме формулы (2.8), пользоваться формулой:

τmax =	1	(σx −σy )2 + 4τ2xy .	(2.8а)
	2

Определение главных напряжений при плоском напряженном состоянии по исходным напряжениям на произвольных площадках (рис.2.2) проводится по формуле (2.9), в которой знак «+» перед радикалом дает значение σmax , а знак «–» – значение σmin .

σi (σj )=

σ

x

+ σ

y

σ

x

−σ

y

2

±

+ τ2xy .

(2.9)

2

2

Направление главных напряжений (положение главных площадок) определяется по формуле:

	tg 2α0 =	−2τxy	.	(2.10)
		σx −σy

В формуле (2.10) индекс x в качестве «адреса» стоит на первом месте у τ , в силу чего обязательно σx должно стоять на первом

месте в знаменателе. Отсчет угла α0 производим от направления

σx (от оси x), т.е. α0 = (σx ,σi ). Если же у τ будет «адресом» y, то на первое место в знаменателе нужно поставить σy . Отсчет уг-

лов α0 будет производиться от направления σy (от оси y).
Если в знаменателе	σx −σy > 0 , то	получаем	α0 max =
= (σx ,σmax ), и наоборот,	если σx−σy<0 ,	то получаем	α0 min =

= (σx ,σmin ).

Главное напряжение σmax всегда лежит в пределах угла 45° ме-

жду главной диагональю касательных напряжений и направлением наибольшего по алгебраической величине исходного нормального

напряжения; так если σx	> σy , то σi = σmax , как показано на
рис. 2.2, и α0=α0 max . Если	σy > σx , то σmax будет располагаться

между главной диагональю и направлением напряжения σy .

72

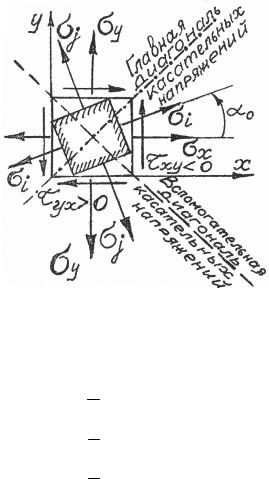
Рис. 2.2

Относительная деформация в случае объемного напряженного состояния определяется по формулам обобщенного закона Гука:

ε

ε

ε

x= E1 σx

y= E1 σy

z= E1 σz

−μ(σy + σz ) ;
−μ(σz + σx ) ;	(2.11)
−μ(σx + σy ) .

Если помимо механического воздействия имеет место одинаковое изменение температуры во всем объеме тела на t , то к каждому выражению ε формулы (2.11) нужно добавить слагаемое α t , где α – коэффициент линейного расширения. Это следует

	из того, что, например, εx (t )=	l (t )	= α	t l	= α t .
		l		l
		73

Аналогично формуле (2.11), ε выражается и через главные напряжения, так, например, по направлению действия σi будем иметь

εi =	1		σi −μ(σj + σk ) .	(2.11а)
	E

Формулами (2.12) представлен закон Гука при сдвиге:

γxy =	τxy	,	γyz =	τyz	,	γzx =	τzx ,	(2.12)
	G			G			G

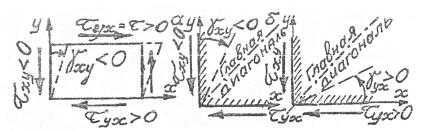
где γ – угол сдвига, знак которого определяется знаком касатель-

ного напряжения. Как и угол α в формулах (2.6) и (2.7), положительный угол γ откладывается против часовой стрелки, а отрица-

тельный – по часовой стрелке. Так как угол γ представляет собой

угол поворота грани элемента, то он и откладывается от соответствующей грани, определяемой нормалью к этой грани (рис. 2.3).

Рис. 2.3 Рис. 2.4

Рассмотрим изменение прямого угла у главной диагонали каса-

	тельных напряжений. При фиксированной грани y γxy =					τxy	< 0	,
						G
		показано на рис. 2.4, а; или при фиксированной						x
	как				грани
	γyx	=	τyx	> 0 , как показано на рис. 2.4, б. Изменение прямого угла у
			G

вспомогательной диагонали показано на рис. 2.5, а при фиксированной грани y, и на рис. 2.5, б при фиксированной грани x.

Обращаем внимание на выделенный союз или, которым подчеркиваем, что прямой угол у главной диагонали уменьшается на

74

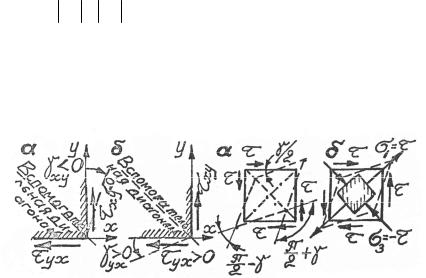
угол γ = γxy = γyx , а прямой угол у вспомогательной диагонали

увеличивается на γ . Таким образом, у элементарной призмы с

квадратным основанием последнее превращается в ромб в результате действия касательных напряжений (рис. 2.6, а). Это соответствует и результату действия главных напряжений при чистом сдвиге

(рис. 2.6, б).

Рис. 2.5

Рис. 2.6

Относительное изменение объема вычисляется по формуле:

εV =

V

= ε1 + ε2 + ε3 = εx + εy + εz =

1 − 2μ(σx + σy + σz )=

V

E

=

1 − 2μ(σ + σ

2

+ σ

3

)=

1 − 2μ I

I

,

(2.12)

E

1

E

где V – объем до деформации.

Если имеется и изменение температуры, то к формуле (2.12) нужно добавить слагаемое 3α t .

Относительное изменение площади в плоскости действия пары главных напряжений σi , σj определяется равенством:

εF = εi + εj ,

(2.13)

где εi , εj определяются по формулам вида (2.11а).

С учетом значения εV можно представить обобщенный закон Гука в форме напряжений, выраженных через деформации (2.14):

75

σ

x

= λ ε + 2Gε

x

;

V

σy = λ εV

+ 2Gεy ;

(2.14)

σ

z

= λ ε + 2Gε

z

,

V

где λ =

E μ

– постоянная Ламе.

(1 +μ) (1 − 2μ)

Удельная потенциальная энергия деформации:

u =

U

=

1

σ2 + σ2

+ σ2

−

2μ(σ σ

+σ

σ

+σ

σ

)

=

V 2E

1

2

3

1 2

2

3

2

3

= G

ε2

+ε 2

+ ε 2

+

μ

ε2

=

1

2

3

1 −

2μ

V

(2.15)

= 1 − 2μ(σ + σ

= u

+u

Φ

2

+σ

3

)2 +

V

6E

1

1 +μ

+

(σ −σ

2

)2 +(σ

2

−σ

3

)2

+(

σ −σ )2

,

1

3

1

6E

где uV – удельная потенциальная энергия изменения объема, а uΦ – удельная потенциальная энергия изменения формы.

2.2. Задачи

Задача 2.1. Определить вид напряженного состояния и значения главных напряжений (рис. 2.7).

Задача 2.2. Определить величину и направление наибольшего главного напряжения (рис. 2.8).

Задача 2.3. Найти соотношение между σx , σy , τxy , при кото-

ром будет иметь место линейное напряженное состояние (рис. 2.9). Задача 2.4. Как изменится первоначально прямой угол АВС при приложении к стержню осевой растягивающей силы P (рис. 2.10).

Даны P, F, E, G, μ .

Задача 2.5. Определить напряжения в наклонных площадках бруса квадратного поперечного сечения при осевом растяжении силой P (рис. 2.11).

76

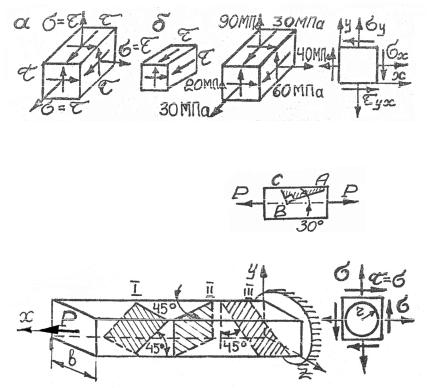
Рис. 2.7

Рис. 2.8

Рис. 2.9

Рис. 2.10

Рис. 2.11 Рис. 2.12

Задача 2.6. Найти размеры и направления полуосей эллипса, в который превращается начерченная окружность (рис. 2.12) при деформации элемента, если σ, E, μ известны.

Задача 2.7. Определить τmax в изображенном элементе (рис. 2.13)

и указатьположение площадки, накоторомонодействует.

Задача 2.8. Брус в форме правильной трапеции и толщиной t = = const (рис. 2.14) сжимается силой P, равномерно распределенной по верхней площадке бруса. Показать, что, кроме σx , возникают

напряжения σy и τxy в сечениях бруса.

77

Рис. 2.13

Рис. 2.14

Рис. 2.15

Задача 2.9. Определить изменение длины упругого стержня, на левую часть которого длиною a действует всестороннее давление p (рис. 2.15). Размеры и упругие постоянные известны.

Задача 2.10. Длинная резиновая лента, имеющая в свободном состоянии длину l, ширину b и толщину δ, наматывается с постоянным натяжением силой P на жесткий валик диаметром d. Выяснить, какой диаметр D получится после того, как вся лента будет намотана на валик? Принятьдлярезины μ = 0,5 ; значенияE, P, l, b, δ известны.

Задача 2.11. Доказать, что при сжатии стержня вдоль оси абсолютноеизменениеобъеманезависитотплощадипоперечногосечения.

Рис. 2.16

Рис. 2.17

Рис. 2.18

Задача 2.12. Определить соотношение между главными напряжениями, при котором длины диагоналей прямоугольного элемента (рис. 2.16) не изменяются в случаях, если материал элемента – сплав ниобия ( μ = 0,39 ), или ковкий чугун ( μ = 0,36 ). Изобра-

зить напряженные состояния.

78

Задача 2.13. При каком соотношении между σx , σy , σz возник-

нет одноосная деформация в изображенном элементе (рис. 2.17)? Задача 2.14. В паз абсолютно жесткой плиты (рис. 2.18) встав-

лен упругий кубик с ребром a. Под действием равномерно распределенного по верхней грани давления p верхняя грань опускается

на δ = k a , где k = 3 (1 −μ2 ) 10−4 . Определить p и положение волокна АВ на боковой грани кубика, в котором отсутствует продольная деформация. E = 2 105 МПа, μ = 0, 25 .

Задача 2.15. К упругому кубику задачи 2.14 приложено по верхней грани сжимающее давление p, а на свободных вертикальных гранях растягивающее равномерно распределенное усилие

P = 3 pa2 . Найти изменение размеров ребер кубика.

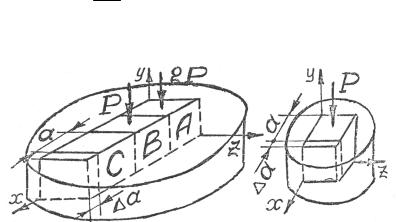
Задача 2.16. В гнездо, имеющее вид прямоугольного параллелепипеда, в абсолютно жесткой плите вставлены три упругих одинаковых кубика А, В, С с ребром a. Кубик В сверху нагружен силой P, равнораспределенной по его верхней грани, аналогично нагружен кубик А, но силой, равной 2P (рис. 2.19). До нагружения куби-

ков зазор a << PE μa . Определить напряжения на гранях всех ку-

биков, если E, μ , a, P, a известны.

Рис. 2.19

Рис. 2.20

Задача 2.17. В гнездо абсолютно жесткой плиты вставлен упругий кубик с ребром a. На верхнюю грань кубика действует сила P,

79

равномерно распределенная по грани, под действием которой верхняя грань опускается на 3 a . До нагружения имелся зазор

размером a (рис. 2.20). Определить P, если E, μ , a, a заданы.

	Задача 2.18. В стакан, стальной
	толстостенный (EF = ∞), (рис. 2.21)
	помещен без зазора упругий мате-
	риал, сверху положена абсолютно
	жесткая крышка диаметром d, через
	которую силой P материал сжат.
	Определить, насколько поднимется
	(опустится) крышка, если материал
Рис. 2.21	нагреть до температуры t. Известны
	P, l, d, E, μ , t, коэффициент линей-

ного расширения α .

Задача 2.19. Брусок квадратного поперечного сечения (a = 4 см) жестко заделан сечениями А и D (рис. 2.22). На участке ВС испытывает всестороннее давление p = 100 МПа. Определить переме-

щение ux (B). E = 2 105 МПа, μ = 0,3 .

Рис. 2.22

Задача 2.20. Полый куб сделан из листового металла и подвержен внутреннему и внешнему давлению p. Определить изменение внутреннего объема куба, если дано E, μ , p, a – размер ребра куба.

Толщина листа намного меньше размера a.

80