Исаченко Сопротивление материалов ч.1 2010

Очевидно, что перемещение точки A (U yA ) складывается из де-

формации участка AD и DH стержня 1. Для того чтобы избежать ошибки в оценке вклада участков в перемещение точки A, воспользуемся приемом временнóго отвердевания. Пусть участок AD стержня 1 превратился в абсолютно твердое тело. Сечение D стержня переместится вниз настолько, насколько растянется участок DH, т.е.

	Nx′		2	l
			3
U yD = l1′ =	1				,
	E1F1

на столько же (так как участок AD абсолютно твердый) переместится вниз и точка A. Очевидно, что в действительности точка A сместится вниз на меньшую величину, так как участок AD упругий

						Nx′′			1	l
и под действием	Nx′′	сожмется на	l1′′=			1 3					.
	1					E1F1
Таким образом,
		U yA = AA1 =	l1′ −			l1′′		.	(1.57)

Для составления дополнительного уравнения проведем вспомогательную прямую A2C1 & AC , тогда

AA −CC BB −CC

l1′ −

l1′′

− l3

l

−

l

1

1

=

1

1

или

=

2

3 . (1.58)

a +b

b

a +b

b

Выражая согласно закону Гука

li

через Nx

в уравнении (1.58)

i

и решая совместно с уравнениями (1.53), (1.54) и (1.55), найдем искомые усилия в стержнях.

1.3.9. Задачи «Диски»

Пусть требуется определить усилия в стержнях 1, 2, 3, поддерживающих абсолютно жесткий брус AK, весом которого по сравнению с величиной P пренебрегаем (рис. 1.17, а).

Начнем решение задачи с изображения деформированной системы, для чего мысленно заменим брус AK диском (рис. 1.17, б). В диске проводим радиусы rB и rC из точки K, вокруг которой диск

41

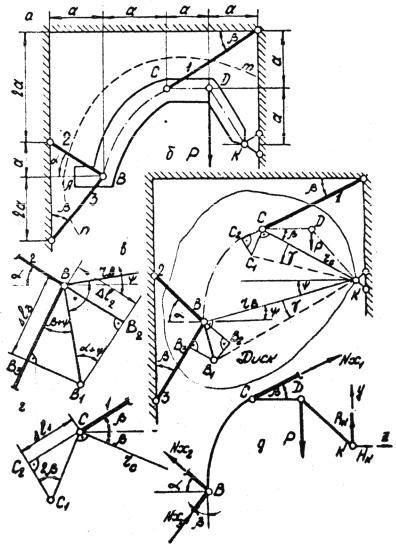
Рис. 1.17

42

поворачивается на некоторый небольшой угол γ (величина угла поворота диска определяется деформациями стержней). Любой радиус в диске, проведенный из точки K, повернется на угол γ. Новое положение точек B и C найдем, проведя BB1 BK и C1C CK –

перпендикуляры к первоначальному положению подвижных радиусов. Способом раскрепления узла строим у шарниров B и C диаграммы перемещений (рис. 1.17, в, г), откуда следует, сто стержни 1 и 2 испытывают растяжение, а стержень 3 – сжатие.

Принимая за объект равновесия брус AK и выделяя его сечением n − m по стержням, получаем силовую схему (рис. 1.17, д), для которой можно составить три уравнения равновесия, а именно:

n	n	n
∑Yi = 0 ,	∑Zi = 0 ,	∑MK = 0 .	(1.59)
i=1	i=1	i=1

В них войдут пять неизвестных Nx1 , Nx2 , Nx3 , RK и HK , т.е. за-

дача два раза статически неопределимая.

Дополнительные уравнения получим из диаграммы перемеще-

ний (рис. 1.17, в)

BB1

=

l2

=

l3

,

(1.60)

sin(α+ ψ)

cos(β+ ψ)

а также из подобия треугольников BKB1 CKC1

(две пары углов

соответственно

равны)

в деформированной

системе

(см.

рис. 1.17, б)

CC1

=

BB1

или

l1

=

l2

,

(1.61)

r

r

cos 2βr

sin(α + ψ)r

C

B

C

B

где

li = Nxi li . Ei Fi

Очевидно, что разд. 1.3.3 – 1.3.7 – частные случаи задач «дисков», в которых все стержни прикреплены к одному подвижному радиусу диска (отрезок прямой AK на рис. 1.11 и 1.15).

43

1.4. Интеграл Мора для определения перемещений

Использование интеграла Мора в большинстве случаев рассматривается в темах изгиба, сложного сопротивления и т.д., хотя он вполне применим для темы растяжения.

1.4.1. Решение статически определимых задач

При наличии только одного внутреннего силового фактора Nx интеграл Мора имеет вид

	Nx
n		N		i	dx
δ = ∑ ∫	j			j		,	(1.62)
	E j Fj
j=1 l j

где Nx j – выражение внутреннего силового фактора на j-м участке

(стержне) от заданной нагрузки; Ni j – выражение внутреннего си-

лового фактора на j-м участке от единичной (безразмерной) силы, приложенной в i-м сечении в направлении искомого перемещения; l j и E j Fj – длина и жесткость поперечного сечения j-го участка

(стержня) соответственно.

Для стержневых систем, элементы которых испытывают только деформацию растяжения-сжатия от сосредоточенных сил, формула (1.62) имеет вид

	Nx				l j
		N		i
δ = ∑	j			j		,	(1.63)
	E j Fj

которая была предложена Максвеллом. Верещагином был предложен графоаналитический способ вычисления интеграла Мора в случае, если оси стержней прямолинейны и жесткость EF постоянна или кусочно-постоянна. Согласно способу Верещагина интеграл Мора может быть вычислен по формуле

			iC
n	ωj N
δ = ∑			j	,	(1.64)
j=1	E j Fj

где ωj – площадь так называемой грузовой эпюры, т.е. эпюры Nx от действующих нагрузок; NiCj – ордината эпюры нормальной силы Nx

44

на j-м участке от единичной силы, под центром тяжести грузовой площади ωj ; единичная сила приложена в i-м сечении, перемещение

которогоопределяетсяи внаправлении искомого перемещения. Операцию в числителе формулы (1.64) принято называть «пере-

множением» эпюр.

Покажем как для стержня, изображенного на рис. 1.18, а, определяется перемещение, например, сечения K в направлении оси x с помощью способа Верещагина. Покажем именно возможность, а не как рекомендацию к рациональному решению (см. вариант 2 к данному примеру). Расчетная схема представлена на рис. 1.18, б; жесткость поперечного сечения на участке AB равна 2EF, а на участке BK – EF. Из уравнения равновесия в виде ∑x = 0 , получим, что

RA = ql . На рис. 1.18, в изображена эпюра Nx (грузовая площадь).

На рис. 1.18, г дана единичная система. В сечении K (сечение i-е перемещение которого будем определять) приложена единичная сила P° =1 по направлению x (по направлению искомого перемещения).

На рис. 1.16, в показаны положения центров тяжести C1 , C2 , C3

грузовых площадей. Отметим, что для этой задачи определять положения центров тяжести нет смысла, так как где бы они не нахо-

дились,

ординаты

на

эпюре

N

x

везде

одинаковы, т.е.

N

C

= NC

2

= NC =1 .

1

3

По формуле (1.64)

U

=

1

+

1

K

ω N

C

(ω N

C

+ ω N

C

) =

2EF

1

EF

2

3

2

1

1

25 ql2

1

3

ql

2

1

5

ql

2

1 +3ql

2

=

1

+

1

=

.

2EF

2

2

4 EF

EF

Знак «+» в результате указывает, что направление перемещения сечения K совпадает с направлением единичной силы P° =1 .

Вариант 2 решения. Исходя из принципа суперпозиции (принципа независимости действия сил) и учитывая формулы (1.8) и (1.9) определим UK :

UK = −

ql2

(ql) l

ql2

P l

P 2l

25 ql2

−

−

+

+

=

.

2

2EF

2EF

2EF

2EF

EF

4 EF

45

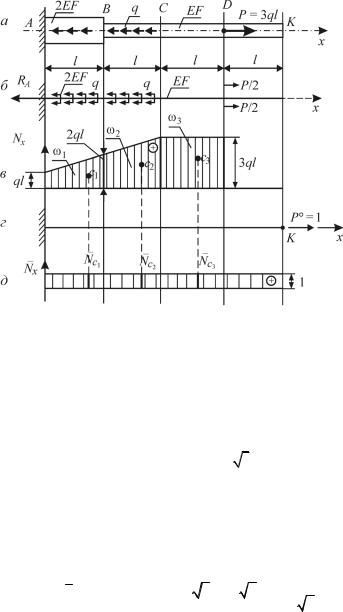
Рис. 1.18

Откуда делаем вывод, что при решении задачи нужно выбирать менее трудоемкий и более компактный способ решения.

Для стержневой системы в виде кронштейна (рис. 1.19, а) необходимоопределить вертикальноеи горизонтальноеперемещения узлаB.

Вариант 1. При решении воспользуемся способом Верещагина. Из рассмотрения равновесия узла B (рис. 1.19, б) в виде уравне-

ний ∑Z = 0 , ∑Y = 0 получим, что Nx =	3P , Nx	2	= 2P . Эпюры
1

Nx (грузовые площади) представлены на рис. 1.19, в. Для опреде-

ления вертикального перемещения узла B изобразим единичную систему (рис. 1.19, г) с силой P° =1 , приложенной к узлу B по вер-

представлены на рис. 1.19, д.

тикали; эпюры N

x

По способу Верещагина

δB =

1

(ω1N

C

)=

1

3P l

3 + 2P

2

l 2 =

+ ω2 N

C

2

EF

1

EF

3

46

				8		Pl	.
	=	3	+
				3		EF

Для определения горизонтального перемещения изобразим единичную систему, загруженную силой P° =1 по горизонтали (рис. 1.19, е). Из рассмотрения равновесия узла B (рис. 1.19, ж) по-

лучим, что Nx′1 = P° =1 , а Nx2 = 0 . Эпюра Nx для этой единичной системы представлена на рис. 1.19, з.

Рис. 1.19

47

δГ = EF1 ω1NC′1 = EF3Pl .

Вариант 2. Из условий равновесия узла B имеем, что

Nx

=

3P , Nx

2

= 2P . Тогда

1

Nx l1

Nx

l2

3P l

2P l

4Pl

l

=

1

=

, l

2

=

2

=

=

.

1

EF

EF

EF

cos30°EF

3EF

Изобразим деформационную систему и построим диаграмму перемещений (рис. 1.20).

Рис. 1.20

Из диаграммы перемещений имеем, что

δГ = l1 = EF3Pl ;

l

l

3P l

3

4Pl 2

8

Pl

δB =

1

+

2

=

+

=

3

+

.

tgα

sin α

EF 1

EF

3EF 1

3

1.4.2. Статически неопределенные многостержневые системы при растяжении-сжатии (канонические уравнения метода сил)

План решения состоит из следующих операций.

1.Отбрасывая «лишние» связи, стоим основную систему.

2.Загрузив основную систему всеми внешними нагрузками, в том числе «лишними» неизвестными, которые заменили «лишние»

48

связи, получаем эквивалентную систему. При этом «лишние» неизвестные переходят в категорию внешних активных сил.

3. Записываем канонические уравнения метода сил.

Для n раз статически неопределимой системы уравнения имеют вид:

δ11X1 + δ12 X2 +... + δ1n Xn +	1p = 0 ;	(1.65)
δ21X1 + δ22 X2 +... + δ2n Xn +	2 p = 0 ;	(1.66)
…

δn1X1 + δn2 X2 + δnn Xn + np = 0 .

Уравнение (1.65) представляет собой перемещение точки приложения силы X1 в направлении этой силы. Аналогично уравнение

(1.66) – перемещение точки приложения силы X2 в направлении этой силы и т.д.

В уравнениях: ip – грузовое перемещение только от заданной

внешней нагрузки в эквивалентной системе, определенной в точке приложения и в направлении неизвестной силы Xi ; δii – главное

единичное перемещение (главные коэффициенты канонического уравнения), которое представляет собой перемещение i-й точки от единичной силы в направлении Xi силы; δij – побочные единич-

ные перемещения (побочные коэффициенты канонического уравнения), которые представляют собой перемещения i-й точки (точки

приложения силы Xi	и в направлении Xi от единичной силы, на-
правленной так же, как и X j . Отметим, что δij = δji .
Для определения	ip , δii , δij необходимо построить эпюры Nx

от только заданной нагрузки для эквивалентной системы, т.е. построить грузовые площади; построить эпюры Nx от единичных

усилий для основной системы, загруженной только единичными силами, приложенными в (i, j) точке по направлениям i, j, …, n. Далее следует произвести, например, по способу Верещагина пере-

множение эпюр, т.е.	для получения ip перемножить грузовую
эпюру Nx с эпюрой				от i-й единичной силы; для получения
	N		x
			i
δii – перемножить эпюру
				N		x от X1 =1 саму на себя; а δij полу-
						i
				49

										. Подчеркнем, что все
чим, перемножив эпюру N					x	на эпюру Nx			j
					i
			относятся к эпюрам от единичных усилий. При пере-
эпюры N		x
		i

множении следует учитывать знаки эпюр.

В самом общем виде канонические уравнения записываются так

[15]:

n

∑δjk Xk +

jp = 0 ,

j =1, 2, 3, ..., n .

(1.67)

k=1

T , то канонические

Если в системе температура изменяется на

уравнения принимают вид

n

∑δjk Xk +

jT = 0 ,

(1.68)

k=1

где

jT

– температурное перемещение в основной системе в на-

правлении X j , и может быть вычислено по формуле:

m

jT

= ∑αi

Ti N

jjli ,

(1.69)

i=1

где

αi

– температурный коэффициент линейного расширения на

j-м участке (в i-м стержне);

jj –

Ti – изменение температуры; N

x от действия

нормальная сила N

единичной

силы

X j = P° =1 ,

приложенной в направлении действия «лишней» неизвестной; li – длина участка, на котором происходит изменение температуры.

При наличии монтажного зазора j в направлении X j каноническое уравнение запишется:

n
∑δjk Xk = − j .	(1.70)

k=1

Пример решения с использованием канонических уравнений показан в задаче 1.14, в которой можно убедиться, что решения с помощью канонического уравнения менее трудоемко. Более подробно применение канонических уравнений метода сил будет рассмотрено при решении рамных систем.

50