Исаченко Сопротивление материалов ч.1 2010

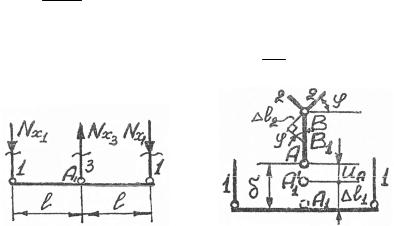
А. Из диаграммы АА	=		l1	=	l2	; l =	h	, l =	h	, откуда
1		cosβ			cos α	1	sin β	2	sin α
sin 2α = sin 2β α = 90 −β ( α =β не имеет смысла).
1.10. 1. Определим			тип		задачи		по	формуле		(1.13):
S = 3K − Ш =1 , так как K = 4 ,					Ш =11 , т.е. задача один раз стати-
чески неопределимая.

2. Выделяем объекты равновесия (рис. 1.50, 1.51) и составляем для них уравнения равновесия в виде ∑y = 0 , т.е. получаем два

уравнения.

3. Изобразим деформационную схему (рис. 1.52). На схеме А1′ –

	положение шарнира		А после сборки (после присоединения к А1 ).
	Отрезок BB1 = uB	–	перемещение шарнира В. Дополнительное
	уравнение будет иметь вид:						l2
	δ = l +u	A	= l + (u	B	+ l ) =	l +		+	l ,
	1		1		3	1	sin ϕ		3

где li = NEFxi li .

4. Решая совместно уравнения п.2 и 3, найдем монтажные уси-

лия Nxi , а напряжения по выражению σxi = NFxi .

Рис. 1.51 Рис. 1.52

1.11. 1. Определяем тип задачи по формуле (1.13): S = 3K − Ш =1 (так как K = 2 , Ш = 5 ) – задача один раз статически неопределимая.

61

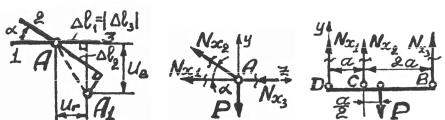
2. Построим диаграмму перемещений (рис. 1.53). А1 – новое положение узла А. Запишем дополнительные уравнения: l1 =

						l		l		Nx li
=		l		, АА	=	1	=	2	, где l =	i	.
		3		1		sin γ		sin (α + γ)	i	EF

3. Выделим объект равновесия – узел А (рис. 1.54) и направим усилия в строгом соответствии с деформационной схемой (см. рис. 1.53); составим уравнение равновесия в виде ∑y = 0 , ∑z = 0 .

4. Совместное решение уравнений п.2 и 3 дадут Nx1, Nx2 , Nx3 , γ .

5. Определим uгор = l1 , uвер =	l1 / tgγ .
1.12. 1. Из условия задачи l1 =	l2	Nx	= Nx .
		1	2

2. Изобразим силовую схему (рис. 1.55). Уравнения равновесия

для нее ∑y = 0 , ∑mc = 0 , откуда Nx = Nx	2	= 0,3P ,
1

Nx3 = 0, 4P > Nx1 .

3. Величина, на которую нужно стяжной гайкой поднять сече-

	ние	B стержня 3, будет равна δ =		l3 −	l1 =	l	(Nx3 − Nx1 )=
						EF
		Pl
	= 0,1		.
		EF

Рис. 1.53

Рис. 1.54

Рис. 1.55

1.13. 1. Введем обозначения: l1 = l , l2 = 2l , sin α = 2l sin πn , где n – число сторон многоугольника.

62

2. Определим тип задачи по формуле (1.13): S = 3K − Ш =1 , так как K =8 , Ш = (8 −1)+(3 −1)8 = 23 , т.е. задача один раз статически неопределимая.

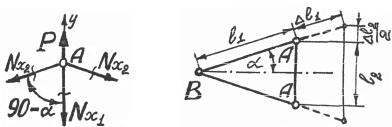
3.Выделим объект равновесия – узел А (рис. 1.56) и составим уравнение равновесия в виде ∑y = 0 : P − Nx1 − 2Nx2 sin πn = 0 .

4.Построим диаграмму перемещений (рис. 1.57) и составим до-

l

2

π

Nx

li

полнительное уравнение:

=

l

sin

,

где

l =

1

, откуда

2

1

n

i

EF

P

Nx

= Nx

; тогда из уравнения равновесия

Nx

= Nx

=

.

π

1

2

1

2

1

+ 2sin

n

5. Такой же результат можно получить, воспользовавшись феноменологическим приемом:

l1 +

l1

=

l1

,

или

l1 +

l1

=

l2 +

l2

,

l +

l

l

l

2

l

2

2

2

1

Nx

Nx

или

1+ ε =1+ ε

2

,

или

1

=

2

,

1

EF

EF

откуда Nx

= Nx .

1

2

Рис. 1.56

Рис. 1.57

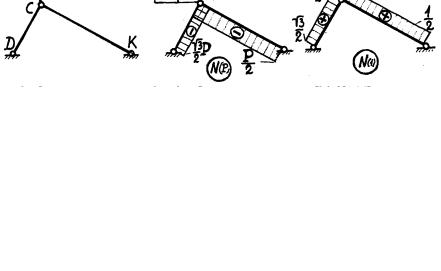
1.14.Вариант 1. Из равновесия узла C (рис. 1.58, а)

∑Z = 0 ; N3 sin β− N4 sin ϕ = 0 ;

63

∑Y = 0 ; −P + N3 cosβ+ N4 cos ϕ = 0

получаем N3 = P3 3 , N4 = P2 .

Рис. 1.58

Из диаграммы перемещений (рис. 1.58, б) имеем:

CC1

=

U (C)

=

l3

=

l4

,

cos γ

cos(β+ γ)

cos(ϕ− γ)

откуда

tgγ =

U (C)cosβ− l3

=

l4 −U (C)cos ϕ

.

U (C)sin β

U (C)sin ϕ

С учетом значений синусов и косинусов, указанных в условии задачи углов, получаем из последнего уравнения

2 U (C) = l3 3 + l4

или

2

α

t (l

+ l

2

) −

N2

l2

=

N3 l3

3

+

N4 l4

,

(*)

1

E

F

E F

E F

где

l

=l

AB

= 3 l ,

l

= l

BC

=

l

,

l

= l

=

4l

, l

= l = 4l

(см.

1

2

2

2

3

CD

3

4

CK

рис. 1.34 на с.54). Тогда из (*) получим

t =

1,6 P

=

1,6 50000

= 20° (нагрев).

α E F

12,5 10−6 2 1011 16 10−4

64

Вариант 2. Воспользуемся методом сил. Система один раз статически неопределимая. Выберем основную систему путем замены неподвижного шарнира A на подвижную шарнирную опору, дающую возможность перемещаться концу A верхнего стержня в вертикальном направлении. Тогда эквивалентная система будет иметь вид, показанный на рис. 1.59, а. Запишем каноническое уравнение

δ11X1 + 1P + 1t = 0 .
Так как в конечном состоянии системы X1 = 0 ,	то это уравнение
примет вид
1P + 1t = 0 ,
где 1P и 1t – перемещения в направлении X1	для основной сис-
темы соответственно при нагружении силой P и нагреве стержня
AC. Для их определения строим эпюры нормальных сил при на-

гружении основной системы единичной силой (рис. 1.59, в) и внешней нагрузкой P (рис. 1.59, б). Находим значения коэффициентов:

	= −	1		P	l	1	+	3	P	4	l	3	+	P	4l	1		= −3,2	Pl	;
1P
					2			2		3		2		2		2			EF
		EF
									1t = 2αl			t .

Рис. 1.59

65

Подставив		1P		и 1t		в каноническое уравнение и решив его от-
носительно		t , получим
t =	1,6P		=			1,6 50 103	= 20	° (нагрев).
	αEF					10−7 2 1011 16 10−4
				1,25

1.15. Очевидно, что сечение посредине длины l не перемещает-

		l				l
	ся, т.е.	ux			= 0 . Тогда сечение посредине		также не перемеща-
			2			2

ется, т.е. ux	l	= 0 и т.д.
4
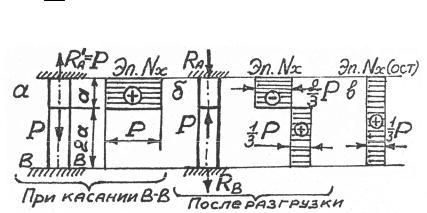
1.16. 1. Из условия			=	Pa	(рис. 1.60, а) получаем P =	EF .
				EF		a
2. После приварки сечения K к B − B и разгрузки (равносильно
приложению силы P			в	противоположном направлении) будем

иметь один раз статически			неопределимую систему (рис. 1.60, б),
решение которой даёт R	A	=	2	P ;	R = 1		P .
			3		B	3

3.Сложив обе эпюры, получили остаточные усилия (рис. 1.60, в)

иσx = NFx (остаточные).

Рис. 1.60

66

1.17. 1. Обозначим через		Н
	q = F γ			– интенсивность равно-
		м

мерно распределенной нагрузки вдоль оси стержня (рис. 1.61, а).

			Рис. 1.61
2. Пусть x0		– координата сечения, отделяющая зону сжатия от
зоны растяжения. x 0 определяется из равенства lсж =											lраст , т.е.
			q x2			q(l − x		)2		откуда x0 = l (2 − 2 ).
согласно формуле (1.9)			0		=		0		,
			2 Ec F			2Ep F
		Nx (σx )
Тогда	эпюра		будет		иметь		вид			(рис. 1.61, б), откуда
RA = q(l − x0 ),		RB = q x0 . Значения нормальных сил в области сжа-
тия	Nx сж = RB −qx ,		в		области			растяжения			Nx раст =

= RA − q(l − x).

3. Перемещения по направлению оси x в области сжатия

x	Nx сж dx		R x			q x2
ux сж = ∫		=	B		−		,	в	области	растяжения
	E F		E	F		2E F
0	c		c			c

	l−x	Nx раст dx				RA (l − x)			q(l − x)2
ux раст = ∫					=			−		. При x = x 0 имеем
		E	F			E F			2E F
	0	p				p			p
ux	сж = ux	раст =		γ l2	(	2 −1)2
							.
0	0				2Ep
								67

Тема 2

АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ. ОБОБЩЕННЫЙ ЗАКОН ГУКА

2.1. Основные положения

Определение главных напряжений осуществляется с использованием характеристического уравнения, называемого иногда «вековым уравнением»:

σ3 −σ2 II + σIII

− IIII

= 0 ,

(2.1)

где инварианты напряженного состояния:

II

= σx + σy + σz

= σ1 + σ2 + σ3 = const ,

(2.2)

III

=

σx

τyx

+

σx

τzx

+

σy

τzy

=

τ

xy

σ

y

τ

xz

σ

z

τ

yz

σ

z

= σ1σ2 + σ2σ3 + σ3σ1 = const,

(2.3)

σx

τyx

τzx

σ

0

0

1

IIII =

τxy

σy

τzy

=

0

σ2

0

= const .

(2.4)

τxz

τyz

σz

0

0

σ3

Корни уравнения (2.1) являются главными напряжениями σi , σj , σk , при этом наибольшему по алгебраической величине присваивается индекс 1 ( σ1 ), наименьшему по алгебраической величине – индекс 3 ( σ3 ), промежуточному – индекс 2 ( σ2 ).

Индексы у напряжений, действующих на произвольных площадках, имеют следующий смысл: при нормальном напряжении – обозначение нормали к площадке, на которой действует напряже-

ние. Так, σx – напряжение, действующее на площадке, нормаль к которой – ось x (параллельна оси x ); индексы при касательном

68

напряжении, например, τxy : первый индекс – это так называемый

адрес, т.е. площадка, на которой действует напряжение, имеет нормалью ось x (или параллельна оси x ); второй индекс обозначает ось, по направлению которой действует касательное напряжение.

В табл. 2.1 приведены виды напряженных состояний.

					Таблица 2.1
Вид напряженного со-	Значение главных		Значение инвариантов
стояния	напряжений		II	III		IIII
Линейное (одноосное)	σi ≠ 0, σj = σk = 0		≠ 0	0		0
Плоское (двухосное)	σi ≠ 0, σj ≠ 0, σk	= 0	Любое	≠ 0		0
Объемное (трехосное)	σi ≠ 0, σj ≠ 0, σk	≠ 0	Любое	Любое		≠ 0

Определение направления главных напряжений получаем из решения системы уравнений (2.5) относительно направляющих косинусов l, m, n:

(σx −σ)l + τy x m + τ zx n = 0;
	τx yl +(σy −σ)m + τzy n = 0;	(2.5)
	τx zl + τy z m +(σz −σ)n = 0;

l2 + m2 + n2 =1.

При использовании в задачах формул (2.1)÷(2.5) следует придерживаться следующего правила знаков для напряжений. Нормальные напряжения положительны, если они направлены от площадки. На площадке, внешняя нормаль к которой направлена в положительном (или отрицательном) направлении соответствующей оси, τ считается положительным, если оно также направлено в положительном (или отрицательном) направлении соответствующей оси.

Определение напряжений на наклонных площадках в случае плоского напряженного состояния, если исходные площадки произвольные, производится по формулам (2.6); (2.6а); (2.7); (2.10) при выполнении следующих правил знаков:

• нормальное напряжение положительно, если оно направлено от площадки, т.е. вызывает растяжение, и отрицательно, если направлено к площадке;

69

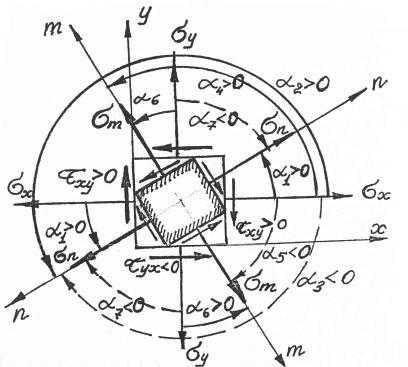
• касательное напряжение положительно, если оно стремится повернуть элемент по часовой стрелке, и отрицательно, если – против часовой; угол α положителен, если направлен против часовой стрелки, и отрицателен – по часовой стрелке (рис. 2.1).

				Рис. 2.1
	σn =	σx +σy	+	σx −σy	cos 2α −τxy sin 2α,	(2.6)
		2		2

где α , с учетом вышеприведенного правила знаков, отсчитывается от того исходного нормального напряжения, которое стоит на первом месте в членах формулы; так, для определения σn можно

взять	угол	α = α1 = (σx , n) > 0 ,	α = α2 =180 + α1 > 0 ,
α = α3 = −(180 −α1 ) < 0 ; для определения			σm можно взять угол

70