Исаченко Сопротивление материалов ч.1 2010

свести к нулю, необходимо чтобы к балке была приложена равномерно распределенная моментная нагрузка интенсивностью m, величину которой найдем из выражения M z для сечения с абсциссой

х: M z = −RA x + M1 + m x = 3 кН·м m = 2 кНм м .

Восстановленная нагрузка на балку и значение опорных реакций приведены на рис. 4.36. Здесь H A = 0 , так как действуют только

вертикальные силы и ∑X = 0 .

4.4. 1. Из эпюры Qy (см. рис. 4.31) следует, что на пролете ЕК действует распределенная нагрузка интенсивностью q(x) .

2. Так как Qy меняется по закону квадратной параболы, то M z должен меняться по закону кубической параболы; общий вид уравнения для M z будет M z = Ax3 + Bx2 + Cx + D , тогда

Qy =

dM z

= 3Ax

2

+ 2Bx + C ,

q(x) =

dQy

= 6 Ax + 2B ,

dx

dx

т.е. q(x) меняется по линейному закону.

3. Найдем коэффициенты А, В, С, D из граничных условий:

при x = 0

Qy = ql (см. рис.4.33) C = ql ,

при x = 0,5l

Qy = 3A(0,5l)2 + 2B 0,5l + C =

ql

,

(1)

при x = l

4

Qy = 3A l 2 + 2Bl + C = −ql

(2)

Решая совместно (1) и (2), получим, что B = −

q

,

A = −

q

.

2

3l

При x = 0 , по условию задачи M z = M E = 0 , откуда D = 0 .

4. Итак, q(x) = − 2lq x − q , т.е. при любом значении х q(x) < 0 (нагрузка направлена вниз), при этом при x = 0 q(x) = −q (значение

интенсивности в сечении над левой опорой Е); при x = l q(x) = −3q (значение интенсивности в сечении над правой опорой К).

191

Qy = ql = RE ; реакция направлена вверх, так как

5. Qy = − ql x2 − qx + ql .

При x = 0

создает положительную перерезывающую силу (стремится повернуть часть балки по часовой стрелке по отношению к сечению с абсциссой х).

При x = l Qy = −ql = RK ; реакция направлена вверх, так как создает отрицательную перерезывающую силу Qy .

Приравняв выражение Qy к нулю, найдем значение абсциссы x0 , при котором Qy переходит через нуль:

−ql x02 − qx0 + ql = 0 x0 = 0,62l .

6.M z = − 3ql x3 − q2 x2 + ql x .

При x = 0 получаем M z = 0 , что соответствует условию задачи.

Рис. 4.37

При x = l M z = 16 ql 2 , т.е. на правой концевой опоре действует сосредоточенный момент M = 16 ql 2 , направленный против часо-

192

вой стрелки, т.е. создающий положительную кривизну оси балки (вода не сливается!).

При x = x0 M z = M z (max) = 0,34ql 2 .

Восстановленная нагрузка на балку представлена на рис. 4.37, а,

аэпюра изгибающего момента – на рис. 4.37, б.

4.2.Напряжения и расчеты на прочность при плоском изгибе

4.2.1. Основные положения

Деформация по высоте сечения балки, расчетная схема которой представлена на рис. 4.38, а, определяется выражением:

	εx =	1	y ,	(4.6)
		ρ

где х – продольная ось балки; у – расстояние от нейтральной n − n оси сечения до рассматриваемой точки поперечного сечения; ρ – радиус кривизны нейтрального слоя, т.е. слоя, не испытывающего ни продольных, ни поперечных линейных деформаций (для него εx = εz = 0 ). Вместе с тем нейтральный слой искривляется при из-

гибе, как в продольном, так и в поперечном направлении (см.

рис. 4.38, г, ж).

Из теории чистого изгиба известно, что кривизна
1		=	M z	,	(4.7)
	ρ		EJ z

где M z – изгибающий момент; J z – момент инерции относитель-

но оси z (нейтральной оси n − n , являющейся главной централь-

ной осью).

Выражение (4.7), по сути, является законом Гука для чистого изгиба. Действительно, умножив правую и левую части выражения

(4.7) на у, получим

1

y =

M z y

1

или εx =

σx

, так как

ρ

J z

E

E

σx =

M z

y

.

(4.8)

J z

193

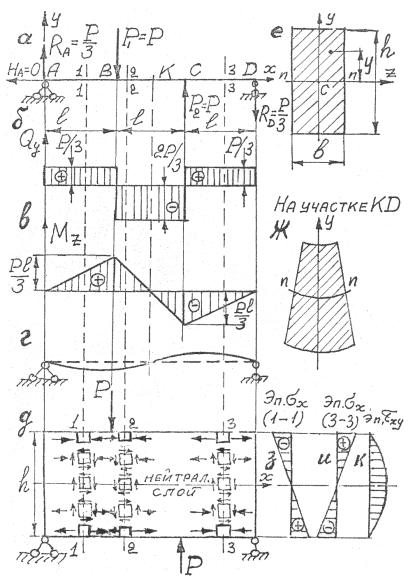
Рис. 4.38

194

При чистом изгибе имеет место одноосное напряженное состояние, продольные волокна испытывают чистое растяжение (сжатие), при этом не надавливают друг на друга, и не сдвигаются относительно друг друга.

По формуле (4.8) определяются нормальные напряжения как при чистом ( M z ≠ 0 , Qy = 0 ), так и при поперечном изгибе

( M z ≠ 0 , Qy ≠ 0 ).

Касательные напряжения при поперечном изгибе определяются формулой Журавского:

	τxy =	Qy S zотс( y)	,	(4.9)
		J z b( y)

где b( y) – ширина сечения на уровне у, т.е. на уровне точки, в ко-

торой определяется напряжение; S zотс( y) – статический момент

относительно оси z отсеченной части площади сечения, лежащей выше (ниже!) уровня у.

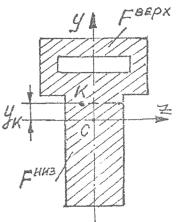
Последнее утверждение («ниже!») подтверждается следующим. Пусть имеем сечение (рис. 4.39), для которого известно положение центра тяжести С, а следовательно, и положение нейтральной оси z. Требуется найти напряжение в точке К, лежащей на уровне у. Статический момент площади всего сечения относительно оси z, как центральной

оси, равен S z = S zверх + S zниз = 0 ,
откуда		S zверх		=		S zниз	Рис. 4.39
							. Очевидно,

что подсчитать S zверх для данно-

го сечения гораздо сложнее, чем подсчитать S zниз, таким образом в этом случае лучше воспользоваться положением «ниже!».

195

Определение знаков нормальных и касательных напряже-

ний. Нормальные напряжения определяем формулой:

σx =		M z	y	,	(4.10)
		J z

где M z и у входят по модулю, о чем памятуя в дальнейшем, записывать будем формулу (4.10) в виде (4.8).

Знак σx определяется эпюрой M z , что и выполним для балки

рис. 4.38, д, где для удобства рассмотрения балка изображена высотой h. Рассмотрим определение знаков напряжений в ряде сече-

ний. В сечении 1 −1 эпюра M z расположена над базовой линией,

т.е. все верхние волокна (волокна выше нейтрального слоя) испытывают сжатие (см. положение 4.3.12 темы 4), а тогда волокна ниже нейтрального слоя – растяжение. Аналогичную картину имеем и

в сечении 2 − 2 . В сечении 3 − 3 эпюра M z располагается под ба-

зовой линией, и следовательно, все волокна ниже нейтрального слоя испытывают сжатие, а тогда волокна расположенные выше нейтрального слоя – растяжение.

Эпюры σx (1 −1) и σx (3 − 3)

представлены на рис. 4.38, з, и. В учебных пособиях можно

встретить и другой прием определения знака σx . В поперечном

сечении в отличие от рис. 4.38, е ось у направляется обязательно Рис. 4.40 вниз, как показано на рис. 4.40. Пользуются формулой (4.8), за-

писывая

M z

и у по алгебраиче-

ской величине. Так, для сечения

1 −1

(рис. 4.38)

M z > 0 ,

yK

> 0 ,

а

y2 < 0 , тогда

1

)

M z yK

M z (− yK

2

σx (K1 ) =

1

> 0 , σx (K2 ) =

< 0 . Математически

J z

J z

все строго, но, по нашему мнению, теряется понимание физического смысла характера деформирования балки при изгибе, да и о не совсем обычномнаправленииосиувнизлегкозабывается.

196

Касательные напряжения τxy в поперечном сечении совпадают

по направлению с перерезывающей силой и, следовательно, их знак определяется знаком Qy .

При решении задач часто пользуются формулами, полученными из условия эквивалентности:

				Qy = ∫τxy dF ,					(4.11)
				F
				M z = ∫σx y dF .					(4.12)
				F
	Основное условие прочности при изгибе имеет вид
		σx (max) =		M z (max) ymax	=	M z (max)		≤[σ] ,	(4.13)
				J z			Wz
		J z
	где Wz =		– неинтегрируемая геометрическая характеристика,
		ymax

так называемый осевой момент сопротивления; очевидно, что чем больше Wz , тем меньше напряжение σx .

С помощью условия прочности (4.13) решаются три задачи.

1.Производится проверочный расчет, т.е. проверяем условие

σx (max) ≤[σ] .

2.Производится проектировочный расчет. Так, из (4.13) имеем,

что Wz ≥ M z (max) /[σ] , а Wz является функцией размеров попе-

речного сечения.

3. Осуществляется расчет грузоподъемности. Из (4.13) имеем,

что M z (max) ≤Wz [σ] , а изгибающий момент M z = f (P, M , q) . Для балок, в которых действуют большой величины касатель-

ные напряжения τxy , что характерно для коротких балок, у кото-

рых в силу малых плеч сил малы и изгибающие моменты, а следовательно, и σx , необходимо проводить проверку по условию прочности по касательным напряжениям.

	τxy (max) =	Qy S zотс(max)	≤[τ] .	(4.14)
		J z b( y)

197

Рис. 4.41

Для балок, имеющих поперечное сечение, например, в виде двутавра (рис. 4.41) проводят проверку прочности и по главным на-

			′
пряжениям для точки K(K ) , где имеет место наиболее неблаго-
приятное сочетание σx (K )			и τxy (K ) :
σ =	σx (K )	+		σ2x	(K)		+ τ2 (K)	≤[σ] .	(4.15)
1	2				4		xy
		4.2.2. Задачи
							Задача	4.5. Металлическую
						полосу (рис. 4.42, а)			нужно
						свернуть в кольцо (рис. 4.42, б),
						не сообщая ей остаточных де-
						формаций. Определить L, если
						известно Е, h, b и все механиче-
						ские характеристики прочности.
							Задача 4.6. Какой размер ши-
						рины b(x)		должен иметь брус,

вырезанный из полосы постоянной толщины h =10 мм и длиной Рис. 4.42 l =1м (рис. 4.43, а), который плотно прилегал бы к цилиндру

198

радиусом R = 5 м под нагрузкой P = 0,5 кН (рис. 4.43, б). Принять

[σ] = 200 МПа, E = = 2 105 МПа.

Задача 4.7. Стальная линейка,

имеющая	поперечное	сечение
0,08 ×5 см2	и длину	l = 25 см,

изгибается в плоскости наименьшей жесткости по дуге в 60º парами сил, приложенными по концам. Определить наибольшее напряжение в линейке.

Задача 4.8. Балка круглого поперечного сечения состоит из сердечника 1 и трубы 2 (рис. 4.44), проскальзывание между которыми не происходит. Балка изгибается моментами М. Найти напряжения в стержнях и построить эпюру напряжений,

если E1 = 4E2 = 4E .	Рис. 4.43
Задача 4.9. Найти τxy (max) и
построить эпюру	касательных

напряжений для балки, испытывающей плоский изгиб. Поперечное сечение балки имеет форму равнобедренного треугольника высотой h и основанием b.

Рис. 4.44

199

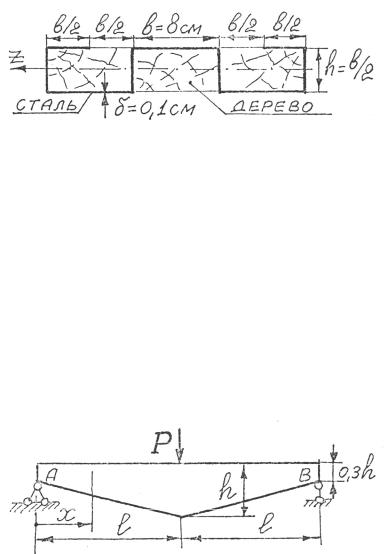
Рис. 4.45

Задача 4.10. В целях использования для балки узких досок была предложена конструкция, приведенная на рис. 4.45. Какой максимальный изгибающий момент выдержит такая балка, если

[σ]ст =120 МПа, [σ]д =13 МПа, Eст = 20Eд ?

Задача 4.11. Из условия прочности вычислить наименьшее допускаемое значение h для балки (рис. 4.46), если P = 20 кН, [σ] =160 МПа, l = 3 м. Поперечное сечение балки – прямоугольник

с постоянной по всей длине балки шириной b = 0,4h .

Задача 4.12. Установить длину двутавровой балки № 20, при которой наибольшие касательные напряжения в точках K1 и K2

будут одинаковыми (рис. 4.47). Показать площадки, по которым действуют эти напряжения, если известно, что для сечения двутав-

ра J z =1840 см2 , S z (max) =104 см3 , d = 0,52 см.

Рис. 4.46

200