Исаченко Сопротивление материалов ч.1 2010

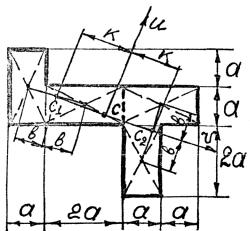
повернутых по отношению друг к другу на 90°. Все построения по определению центра тяжести всей фигуры и положение главных центральных осей приведены на рис. 3.54. Положение 3.1.13 позволяет установить, что u = u(max) , v = v(min) .

Рис. 3.54

3.13. Из таблиц ГОСТа для уголка № 3 (30×30×3), изображенно-

го

на

рис.

3.55, а,

имеем

F =1,74 см2, yc = zc = 0,85 см,

Iz

= I y

=1, 45 см4,

Iz

0

= 2,3 см4,

I y

= 0,6 см4. Тогда

0

I

z

= I

y

= I

z

+ y2 F =1, 45 + (0,85)2 1,74 = 2,707 см4,

c

1

1

yc

S =

=1, 2 см.

sin 45°

Для сечения (рис. 3.55, б) главными центральными осями инер-

ции (см. положения 3.1.3 и 3.1.13) будут оси u и v, для которых

Iv

= 2Iz

= 4, 6 см4 = Imin ,

0

а воспользовавшись формулой (3.9), получим

Iu = 2(I y0

+ S2 F )= 2(0,6 +1, 22 1,74) = 6, 2 см4 = I max .

121

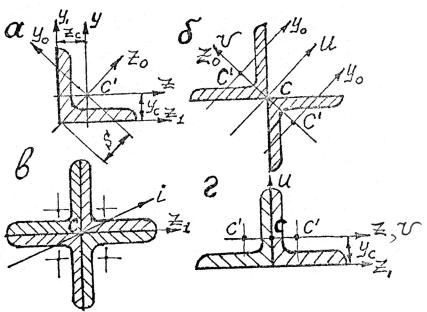
Для сечения (рис. 3.55, в) главными центральными осями будут любые оси, проходящие через точку С (см. положение 3.1.18):

Ii = Iu = Iv = 4Iz1 = 2Iz0 + 2 (I y0 + S2 F )=10,82 см4.

Рис. 3.55

Для сечения (рис. 3.55, г) центр тяжести находится в точке С (см. положение 3.1.3), а главными центральными являются оси u, v, для которых

Iu = 2I y1 = 5,14 см4 = I max ,

Iv = 2Iz = 2,9 см4 = Imin .

3.14.Дополнив сечение обратно зеркальной фигурой (рис. 3.56),

убеждаемся, что заданное сечение является полуфигурой сечения в виде квадрата с квадратным вырезом, и согласно положениям

3.1.16, 3.1.18, а также формуле (3.23) получим

	Iz =	1		(4a)4	−	(2a)4		=10a4 .
		2		12		12

122

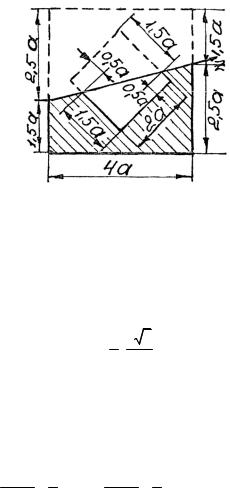
Рис. 3.56

3.15. Сечение, представленное на рис. 3.35, является полуфигурой правильного шестиугольника. Согласно положениям 3.1.6, 3.1.18 и значения момента инерции для шестиугольника (см. решение задачи 3.9) будем иметь, что относительно оси z1 момент инерции

Iz1 = 12 5163 R4 .

3.16.Так как любая центральная ось квадрата является главной центральной осью (см. положение 3.1.18), и любая ось полукруга, проходящая через точку О, является главной осью (см. положение 3.1.19), то для всей фигуры (см. рис.3.36) момент инерции

I y1 = (612a)4 − 12 π4r4 = (612a)4 − 12 π(24a)4 =101,72a4 .

Таким образом, момент инерции относительно оси y1 не зави-

сит от значения угла α.

3.17. Согласно положению 3.1.18 для равностороннего треугольника собственные центральные моменты инерции не зависят

123

от угла α и равны	Ii = bh3 / 36 = 3a4 / 288 ,	так как b = a ,
h = a 3 / 2 . Полярный	момент инерции I′p = 2Ii =	3a4 / 144 .

Воспользовавшись формулами (3.35) и (3.10), найдем полярный момент фигуры (см. рис. 3.37) относительно ее центра тяжести С:

I	p	=	πR4	− 4	(	p		2	)	=	π(4a)4	3a4		+ (2a)	2 1		a	a 3
			2			I′	+ r F′				2	− 4	144		2			2	,

где F′ – площадь равностороннего треугольника со стороной а. Тогда осевой момент инерции фигуры

Iz = I y = I p / 2 .

3.18. Согласно положению 3.1.18 для каждого квадрата, независимо от его поворота относительно главных центральных осей, осе-

			a4
вой момент инерции I	zc	=	i	.
		12

Момент инерции наружного самого большого квадрата с квадратным вырезом (см. рис. 3.38)

a

4

′ 4

a

4

Iz′ =

−

(a )

=

,

12

12

16

где a

′

a

– сторона квадратного выреза, равная 2 .

Размер стороны каждого последующего квадрата с квадратным вырезом в два раза меньше предыдущего, а осевой момент инерции, следовательно, в 16 раз меньше предыдущего. Суммируя моменты инерции всех квадратов с вырезами, получим для всего сечения

	Iz =	a4			1			1			1				a4
			1	+			+			+			+...	=		.
		16			16			162			163				15

3.19. Проведем через точку А оси z, y (рис. 3.57). Согласно положению 3.1.19, если I z = I y , то все оси, проходящие через точку

А, будут главными. Представим фигуру, как состоящую из трех

124

частей: одинаковых прямоугольных треугольников 1 и 3, с катетами а и h, и прямоугольника 2 шириной а и высотой h.

Найдем моменты инерции относительно осей z и y для всей фигуры, воспользовавшись формулами (3.27) – (3.29), (3.9):

		Iz =		ah3	+ 2		ah3			=		ah3				,
				3		12							2
I y =	ha3	ha3			a				a 2					ah				5	ha3 .
		+ 2			+			+									=
	12			36		2							2					6
									3
Из равенства этих моментов найдем h = a																	5 .
																	3

Проверим полученный результат, подставив вместо h его значение:

Iz =	ah3	=	5		5	a4 ;	I y =	5 ha3	=	5	5	a4 .
			6	3						6	3
2								6

Рис. 3.57

3.20. Вариант 1. Проведем через точку О оси z1 , y1 . Эти оси будут главными, так как y1 – ось симметрии (рис. 3.58).

125

Рис. 3.58

Согласно положению 3.1.19, если Iz1 = I y1 (*), то все оси (в том

числе и оси z, y), проходящие через точку О, будут главными. Найдем моменты инерции относительно осей z1 и y1 по форму-

лам (3.26) и (3.27):

I y			HB3		hb3		4t(8t)3				3t a3
	=			−		=			−			,
		12			12			12		12
1
Iz		BH 3			bh3		8t(4t)3			a(3t)3
	=			−		=			−				.
1		3			3			3		3
Из равенства (*) найдем а:
			a = t			108		= 6t .
						3

Вариант 2. По формуле (3.15), с учетом того, что оси z, y должны быть главными,

		Iz	− I y
	Izy =	1	1	sin 2α − Iz y	cos 2α = 0	,	Iz y = 0 .
			2	1 1			1 1
Так как	sin 2α		≠ 0 , то, следовательно, Iz				− I y = 0 , т.е. прихо-
	2				1		1

дим к исходному положению (*) решения варианта 1.

126

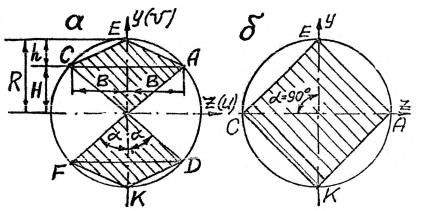
3.21. Оси z, y, как оси симметрии (рис. 3.59, а), являются главными центральными осями инерции, при этом согласно положению 3.1.13 z – ось u(max) , а y – это v(min) . По мере увеличения угла α

величина Iv будет приближаться к значению Iu .	Равенство
Iv = Iu , т.е. I y = Iz (*), наступит при α = 90° (рис. 3.59,	б).

Рис. 3.59

К такому же выводу можно прийти, записав выражение для I y и

Iz для фигуры (см. рис. 3.59, а). Воспользуемся формулами (3.28),

(3.9), (3.30), (3.29), с

учетом,

что

B = Rsin α ,

H = R cos α ,

h = R(1 −cos α) . Тогда

2Bh3

h

2 1

2BH 3

Iz = 2

+

+ H

2Bh +

=

36

3

2

4

=

R4

sin α(1+ cos α +cos2 α);

3

I y

= 4

RB3

=

R4

sin3 α .

12

3

127

Приравняв эти значения, согласно (*) получим cos α(1 + 2cos α) = 0 ,

откуда α1 = 90° или α2 =120° , что для задачи не имеет смысла. 3.22. Пусть искомой точкой на оси y будет точка А (рис. 3.60).

Тогда согласно положению 3.1.20 моменты инерции Iz1 = I y , или, воспользовавшись формулами (3.29), (3.9), запишем, что

			H 3
		B					2		1		9		4		2		2		HB	3	4
Iz	= 2		2			+ a				BH =		b		+ a		3b		= I y =		= 2b		,
		12							2		8								12
1
откуда a = b			7		.
			24

Положение главных осей инерции показано на рис. 3.60.

Рис. 3.60

3.23. Для фигуры (см. рис. 3.43) имеем, что b = 2csin α , h = 2ccos α , b / h = tg α . Момент инерции относительно оси z равен

Iz = 2	BH 3		=		c4 sin αcos3 α		, где B = b , H = h / 2 . Исследуем Iz на
	12					3
				dIz				1		h
экстремум:						= 0 tg2α =			, то тогда		= 3 .
				dα				3		b

128

Момент сопротивления относительно оси z

W

z

=

Iz

= Iz =

Iz

= c3 sin αcos2 α .

ymax

h / 2

ccos α

3

Исследуем

W

z

на

экстремум:

dWz

= 0 tg2 α = 1

, тогда

dα

2

bh = 2 .

3.24. Из рис. 3.61, а имеем, что

b2 + h2 = D2 = 4R2 h2 = 4R2 −b2 .

Отнесем сечение к координатным осям z, y. Брусок прямоугольного сечения будет обладать наибольшей прочностью при изгибе, если момент сопротивления относительно оси z достигнет максимальной величины.

W = I	z	/ y	max	=	bh3	=	bh2	=	b	(4R2 −b2 ) .
z				12h / 2		6		6

Рис. 3.61

129

Из

условия экстремума

dWz

=

2 R2

−

1 b2

= 0 , получим, что

db

3

2

b =

2R

=

D

. Тогда h = b

2

=

D

2

.

3

3

3

Рассмотренную задачу называют задачей Парана (французский ученый, 1666 – 1716). Паран дал ответ в форме, удобной для мастера, работающего топором. Он предложил разделить диаметр на три равные части (рис. 3.61, б), из точек В и С восстановить перпендикуляры BF и CK. Прямоугольник AFEK и будет искомым сечением,

так как b = h2	+(2R / 3)2	= R2 −	1	R2	+	4	R2	=	2R	.
1		9			9			3

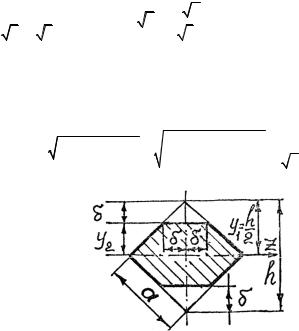
Рис. 3.62

3.25. Для квадратного сечения (рис. 3.62) без удаления площади высотой δ

I	z	=	a4	=	h4	,	W =	Iz	=	h3	.
		12		48			z	y1	24

После удаления площадок высотой δ

I*z

h4

2δ δ3

h

2

2

1

=

−

2

+

−

δ

2δ δ ,

48

36

3

2

2

W *

= I* / y

2

=

1

(24δ3

− 20hδ2 + 2h2δ+ 2h3 ) ,

z

z

24

= h

где

y2

−δ .

2

130