Исаченко Сопротивление материалов ч.1 2010

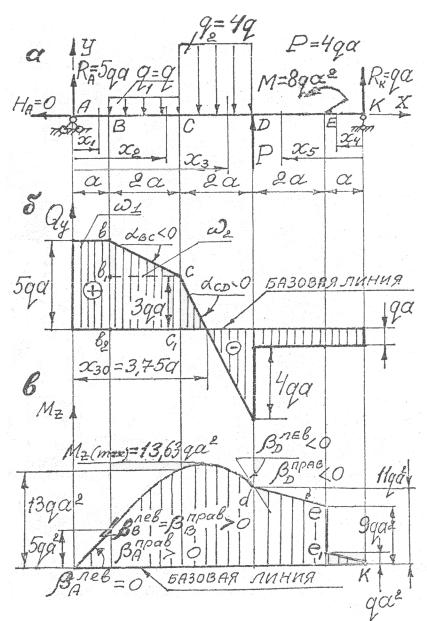
Рис. 4.11

141

∑mC = 0 (где С может быть любой точкой на линии АК) является

следствием тех же уравнений, как сумма моментов относительно точки, лежащей на прямой, соединяющей точки А и К, относительно которых составлены уравнения моментов.1

Зачастую для проверки используют уравнение ∑Y = 0 , однако проводить проверку по уравнению ∑mC = 0 предпочтительнее,

хотя и более сложнее получается само уравнение, но последнее уравнение учитывает и сосредоточенные моменты, которые не входят в уравнение ∑Y = 0 .

Покажем выполнение проверки при использовании как того, так

идругого уравнения:

∑Y = 0 ; RA − 2qa −8qa + P + RK = 0 0 ≡ 0 , или

∑mC = 0 ; RA 3a −2qa a +8qa a − P 2a − M − RB 5a = 0

0 ≡ 0 .

После проведения проверки выносим значения реакций на расчетную схему.

III операция. Составление выражений для поперечной силы

Qy и построение эпюры Qy . Определимся с количеством сило-

вых участков, помня, что силовым участком называется такой участок, на котором сохраняется закон изменения внутренних силовых факторов Qy и M z . Границы участков располагаются в сечениях

приложения сосредоточенных сил, сосредоточенных моментов, начала или конца однородной распределенной нагрузки.

Балка АК (см. рис. 4.11) имеет следующие силовые участки: АВ длиной а, ВС, СD, DE длинами по 2a и ЕК длиной а, т.е. имеем пять силовых участка.

Для составления выражений для поперечной силы, действующей на том или другом участке балки, следует выбрать точку нача-

1 В системе трех уравнений равновесия вида ∑ X = 0 , ∑Y = 0 , ∑ m A = 0

второе уравнение ∑Y = 0 является независимым уравнением, как и в системе трех уравнений равновесия вида ∑ m A = 0 , ∑mB = 0 , ∑mC = 0 (если точки А,

В, С не лежат на одной прямой) третье уравнение ∑mC = 0 также является независимым уравнением равновесия.

142

ла отсчета абсциссы х от левого или правого конца балки, при этом нужно стремиться так выбрать точку отсчета, чтобы в выражение Qy входило по возможности меньшее количество членов. Текущие

абсциссы xi для каждого участка показаны на рис. 4.11, а, при этом абсциссы изменяются в пределах:

0 ≤ x1 ≤ a , a ≤ x2 ≤ 3a , 3a ≤ x3 ≤ 5a , 0 ≤ x4 ≤ a , a ≤ x5 ≤ 3a .

Обратим внимание читателя, что, например, наименьшее значение x2 = a , и не может (!) быть меньше, так как в этом случае он

( x2 ) «заберется в чужой участок», участок «окормляемый» абсциссой x1 . Итак, с учетом правила знаков для Qy имеем:

Qy	= RA = 5qa , т.е. постоянная на всем участке АВ;
1
Qy2	= RA − q(x2 −a)	(линейная зависимость!),
	при x2 = a	Qy	= RA = 5qa ,
	при x2 = 3a	2
		Qy	= RA − q 2a = 3qa ;
Qy		2
	= RA − q 2a − 4q(x3 −3a) (линейная зависимость!),
3
	при x3 = 3a	Qy	= RA − 2qa = 3qa ,
		3
	при x3 = 5a	Qy	= RA − 2qa − 4q 2a = −5qa .
		3

Найдем абсциссу сечения, в котором Qy = 0 , для чего приравняем Qy3 = 0 , откуда x30 = 3, 75a .

Qy4 = Qy5 = −RK = −qa = const .

По полученным данным построим эпюру Qy . Напомним, что эпюра Qy представляет собой графическое изображение закона изменения перерезывающей силы по длине балки.

143

Эпюра Qy строится на базовой линии, параллельной оси балки,

путем отложения по направлению оси Y в соответствующих сечениях найденных значений Qy (см. рис. 4.11, б).

Отметим, что началом отсчета абсцисс силовых участков может служить и начало каждого силового участка. Так, для участка ВС началом отсчета может быть сечение В, при этом абсцисса x2′ име-

ет пределы изменения 0 ≤ x2′ ≤ 2a ; для участка CD с началом в сечении С – 0 ≤ x3′ ≤ 2a и т.п., при этом преимущество по сравнению

с вышерассмотренным выбором начал отсчета в том, что наименьшая величина абсциссы всегда будет «нуль». Существенным недостатком этого «выбора» является то, что обучающийся забывает обо всех других силах, лежащих по одну сторону от рассматриваемого сечения, но не входящих в область x2′ . Поэтому этот способ

отсчета лучше применять при уже имеющемся хорошем навыке в построении эпюр.

Значения ординат эпюры Qy в характерных сечениях (границах участков) можно быстро и легко определить, используя формулу (4.5). Так в этой формуле, например, для сечения С ∫q dx пред-

l

ставляет собой площадь нагрузки q на участке слева от сечения С, т.е. ∫q dx = −q 2a (знак «–», так как нагрузка q направлена сверху

l

вниз, т.е. q < 0 ). Pi = RA = 5qa со знаком «+», так как по правилу

для поперечной силы стремится повернуть левую часть балки по отношению к сечению С по часовой стрелке. Итого имеем в сумме

Qy = −2qa + 5qa = 3qa .

IV операция. Составление выражений для изгибающего момента M z и построение эпюры M z . Рассматриваем те же сило-

вые участки, что и в операции III, с теми же началами отсчета абсцисс текущих сечений и пределами изменения абсцисс xi .

С учетом правила знаков для изгибающего момента имеем M z1 = RA x1 (линейная зависимость!);

144

при x = 0

M

z

= 0 , при x = a

M

z

= 5qa 2 ;

1

1

1

M

z2

= R

A

x

2

− q

(x

2

− a)

(x2 − a)

= 5qa x

2

−

q(x2 − a)2

1

2

2

(квадратная парабола!);

при x2 = a

M z2 = 5qa 2 , при x2 = 3a M z2 =13qa2 .

Рис. 4.12

Рассмотрим применение ранее приведенного правила знаков для установления знаков членов вошедших в выражение M z2 . При оп-

ределении знака момента от того или другого усилия рассматриваем только это усилие, его плечо до сечения, а само сечение мысленно представим себе жесткой заделкой (рис. 4.12). Из рис. 4.12, а

ясно, что R				1
	A	вызывает положительную кривизну			> 0		оси балки
				ρ

(«вода не сливается»!), что изображено штриховой линией, и член RA x2 в выражение для M z2 входит со знаком «+». Из рис. 4.12, б

ясно, что распределенная на длине (x2 − a)			нагрузка интенсивно-
стью q вызывает отрицательную кривизну		1
			< 0		оси балки («вода
		ρ

не удерживается на балке, сливается»!), что изображено штриховой

линией, и член	q(x2	− a)2	входит в выражение для M z2 со знаком
		2

145

«–». Отметим, что при составлении выражения изгибающего момента от распределенной нагрузки, последняя заменяется равнодействующей, приложенной посредине участка длиной (x2 − a) ,

т.е. в центре тяжести площади q(x2 − a) , тогда плечо этой равно-

действующей до рассматриваемого сечения равно x2 2− a .

M

z

= R

A

x

3

− q 2a(x

3

− 2a) −

q2 (x3 − 3a)2

(квадратная па-

1

2

3

рабола!),

= 3qa 2 ,

при x3 = 3a

M z

3

при x3 =5a

M z

3

=11qa 2 .

Найдем еще

одно

значение

M z ,

соответствующее абсциссе

3

x30 = 3,75a . В этом сечении Qy = 0 ,

и согласно дифференциаль-

3

ной зависимости (4.4) M z

достигает экстремального значения.

3

При x3 = x30

M z

3

=13,63qa 2 .

M z4

= RK x4

(линейная зависимость);

при x4 = 0

M z4

= 0 ,

при x4 = a

M z4

= qa .

M z

= RK x5 + M = qa x5 + 8qa 2 (линейная зависимость!),

5

при x5 = a

M z

= 9qa2 ,

5

при x5 = 3a

M z

=11qa 2 .

5

Рассмотрим применение принятого правила знаков для определения знаков членов выражения M z5 . Сечение, лежащее на рас-

стоянии x5 , представим себе жесткой заделкой (рис. 4.13). RK x5 вошло в выражение M z5 со знаком «+», так как этот момент создает положительную кривизну («вода не сливается»!), так же момент M =8qa 2 создает положительную кривизну оси балки.

146

Рис. 4.13

Запомним, что «мысленная жесткая заделка» сечения производится в конце (!) абсциссы xi .

Понайденнымзначениям M zi строимэпюру M z (см. рис. 4.11, в). Значения ординат эпюры M z так же, как ординаты эпюры Qy ,

в характерных сечениях можно легко и быстро определить, используя формулу (4.5). Так в этой формуле, например, для сечения С

∫Qy dx представляет собой площадь эпюры Qy на участке слева

l

от сечения С, т.е.

∫q dx = ω1 + ω2 = 5qa a + 5qa + 3qa 2a =13qa2 = M z (C) . 2

l

Слева от сечения С нет сосредоточенных моментов, поэтому M i в формуле (4.5) равно нулю.

П р и м е р 2 (рис. 4.14)

I операция. Изображение расчетной схемы. Реакции RA и

RC направим вверх (см. рис. 4.14, а).

IIоперация. Определение опорных реакций

∑X = 0 H A = 0 ;

∑mC = 0 : RA 2l − M1 − M 2 = 0 RA = 3Ml ;

∑mA = 0 : RC 2l − M 2 − M1 = 0 RC = − 3Ml .

147

Рис. 4.14

Проверка:

∑Y = 0 : RA + RC = 0 , 3Ml − 3Ml ≡ 0

или

∑mB = 0 : RA l − M1 − M 2 − RC l = 0 ,

	3M			3M
		l − 2M − 4M −	−			l ≡ 0 .
	l			l

Обратим внимание на часто совершаемую грубую ошибку при составлении уравнения равновесия в виде ∑mA = 0 . Записывают

часто это уравнение, не вводя в него момента M1 , полагая, что «так как момент M1 приложен в сечении А, то его момент относи-

148

тельно этого сечения равен нулю», забывая при этом, что это уже «готовый» сосредоточенный момент, и его уже не нужно умножать на какое-либо плечо.

В результате определения реакций получили значение RC со

знаком «–», что свидетельствует о том, что реакция направлена в противоположную сторону. Поэтому, вынося полученные значения реакций на расчетную схему, первоначальное направление реакции RC перечеркнем крестиком, направим RC вниз и запишем ее зна-

чение RC = 3Ml (см. рис. 4.14, а).

III операция. Составление выражений для Qy и построение эпюры Qy . Силовых участков у балки два. Абсциссы текущих се-

чений участков обозначим через

x1

и x2 . Из рис. 4.14, а имеем,

что

0 ≤ x1 ≤ l ,

0 ≤ x2 ≤ l .

Q

y

= R

A

=

3M

= const ,

Q

y

= R =

3M

= const .

l

2

C

l

1

Эпюра Qy представлена на рис. 4.14, б.

IV операция. Составление выражений для M z и построение

эпюры M z .
M z	= RA x1 − M1 (линейная зависимость!),
1	при x1 = 0	M z	= −M1 = −2M ,
		1
	при x1 = l	M z	= RA l − M1 = M ;
		1
M z2	= −RC x2 (линейная зависимость!),
	при x2 = 0	M z2	= 0 ,
	при x2 = l	M z2	= −RC l = −3M .

Эпюра M z представлена на рис. 4.14, в. Покажем, как с помощью формулы (4.5) определить M z1 (B) при x1 = l − 0 , т.е. слева от

сечения (то же сечение В, но справа от сечения имеет абсциссу x1 = l + 0 ).

149

	∫Qy dx = ω1	=	3M	l , M i = −M1 = −2M ,
			l
	l

тогда M z1 (B) = 3M − 2M = M .

П р и м е р 3 (рис.4.15)

Iоперация. Изображение расчетной схемы. В расчетной схе-

ме не будем показывать реакции жесткой заделки (рис. 4.15, а). Изображение сосредоточенного момента другое, чем изображение

впримере 2, но равнозначное ему.

IIоперация. Определение опорных реакций. В жесткой за-

делке возникают три опорные реакции. Горизонтальная реакция

H E = 0 из уравнения равновесия ∑X = 0 , так как на балку дейст-

вуют только вертикальные силы. В консольных балках две другие опорные реакции в защемлении определять не обязательно при вы-

боре начала координат (отсчет абсцисс xi ) от сечения А – конец

консоли, так как полученное далее значение поперечной силы в сечении заделки дает величину и направление вертикальной опорной реакции, а изгибающий момент в сечении заделки – опорный момент в заделке, что и будет показано дальше.

III операция. Составление выражений для Qy и построение эпюры Qy . Силовых участков в балке четыре:

0 ≤ x1 ≤ 2a ,

2a ≤ x2 ≤ 4a ,

4a ≤ x3 ≤ 6a ,

6a ≤ x4 ≤8a .

Абсциссы xi берем только от левого конца балки (от сечения

А) и, таким образом, для всех сечений по одну (левую!) сторону будут только известные внешние усилия, т.е. значения опорных

реакций не будут входить в выражения Qy и M z .

Qy	= −q x1 (линейная зависимость!),
1	при x1			= 0	Qy	= 0 ,
					1
	при x1			= 2a	Qy	= −2qa ;
Qy2	= −2qa = const				1
					на втором участке;
Qy	= Qy	4	= −2qa + P = 4qa = const на третьем и четвертом уча-
3

стке.

150