Исаченко Сопротивление материалов ч.1 2010

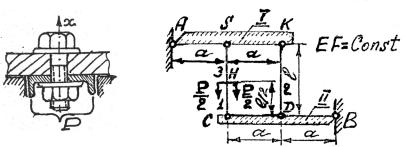
	1.5. Задачи
Задача	1.1. При креплении швеллера к абсолютно жёсткой
(EF = ∞)	плите, в болте, при затяжке гайкой, вызвано растяги-

вающие усилие Nx = N0 . Как будет меняться усилие в болте, если швеллер будет нагружаться силой 0 ≤ P ≤ 4N0 (рис. 1.21)? Построить график Nx = f (P).

Рис. 1.21	Рис. 1.22
Задача 1.2. Доказать, что работа силы P (при статическом на-
гружении от 0 до	P ) численно равна потенциальной энергии де-
формации стержневой системы (рис. 1.22). Дано		P, l, E, F . Де-
формацией и весом балок I, II пренебречь.
Задача 1.3. Построить эпюру Nx с учётом		массы стержня
(рис. 1.23). Дано P, l, m – масса стержня.
Задача 1.4. Абсолютно жесткий (EF = ∞) брус			AB подвешен
на упругом тросе,	пропущенном через блоки C и		D (рис. 1.24).

Дано P, EF для троса, a . Определить положение сечения троса,

которое останется неподвижным при действии силы P . Силами трения, размерами блоков и весом бруса AB пренебречь.

51

Рис. 1.23	Рис. 1.24
Задача 1.5. Брус			AB
(рис.	1.25)	абсолютно
жесткий, весом которо-
го пренебрегаем. Стерж-
ни	1 и	2 упругие
( EF = 2 104 кН), l =1 м.
Определить		силу	P ,

	если при её приложении
	узел B переместился по
	вертикали на 0,08 см.
Рис. 1.25	Задача 1.6. Стержень
	круглого поперечного се-

чения(рис. 1.26, а) имеет по любому диаметру поперечного сечения переменный модуль

E (ρ) (эпюра приведена на рис. 1.26, б). Построить эпюру нор-

мальных напряжений при справедливости гипотезы плоских сечений. P и r заданы.

Рис. 1.26

52

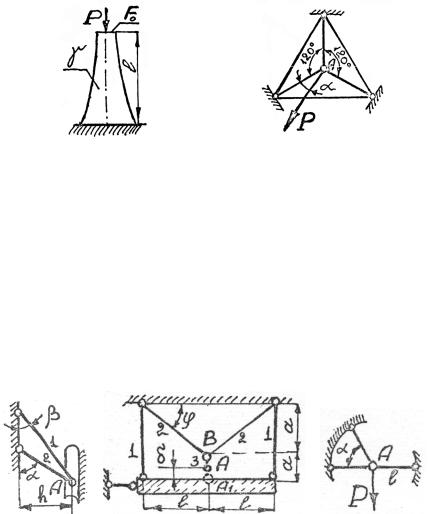
Задача 1.7. Колонна сжимается под действием силы P , равномерно распределённой по верхнему сечению, и собственного веса (рис. 1.27). Требуется подобрать закон изменения площади поперечного сечения колонны из условия равнопрочности. P, γ, [σ] заданы.

Рис. 1.27	Рис. 1.28

Задача 1.8. Доказать, что в стержневой системе (рис. 1.28) узел А перемещается в направлении силы P , если жесткости всех стержней одинаковы.

Задача 1.9. Шарнир А может перемещаться по желобу свободно, но только по вертикали (рис. 1.29). Жесткости стержней одинаковы. При каком соотношении α и β в стержнях не возникают

напряжения при их нагревании на t .

Задача 1.10. Абсолютно жесткая балка, весом которой пренебрегаем, подвешена на упругих стержнях одинаковой жесткости(рис. 1.30). Определить монтажные напряжения, возникающие в стержнях при сборке– при присоединенииточечногошарнира А к А1 ( δ << a ).

Рис. 1.29

Рис. 1.30

Рис. 1.31

53

Задача 1.11. В системе (рис. 1.31) все три стержня имеют одинаковую длину и жесткость. Найти горизонтальное и вертикальное перемещение узла А.

Задача 1.12. На какую величину δ надо укоротить правый стержень, состоящий из двух частей, с помощью стяжной гайки А, чтобы абсолютно жёсткий брус весом P , подвешенный на трех одинаковых стержнях, оставался бы горизонтальным (рис. 1.32)? Известны P, l, α и EF стержней.

Рис. 1.32

Рис. 1.33

Задача 1.13. Определить напряжения в стержнях плоской фермы в виде правильного многоугольника, загруженной в узлах радиальными силами P (рис. 1.33). Жесткость всех стержней одинакова. Длина каждого радиального стержня l .

Рис. 1.34

Задача 1.14. Для стержневой системы (рис. 1.34), линейные и угловые размеры которой известны, определить, как и насколько градусов нужно изменить температуру стержня AC, чтобы на участке AB напряжения стали бы равны нулю. Устойчивость стержней

54

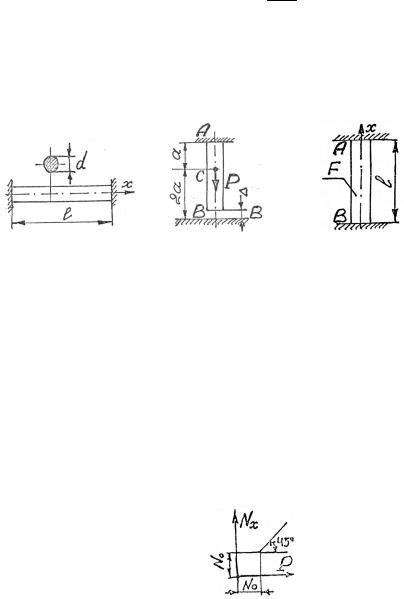
считать обеспеченной. Известно: P = 50 кН, для всех стержней

E = 2 105 МПа, F =16 см2 , α =12,5 10−6 1 .

град

Задача 1.15. Стержень постоянного поперечного сечения жестко заделан правым и левым крайними сечениями (рис. 1.35). Стержень равномерно нагревается по всей длине на t . Показать без

вычислений, что в стержне не возникают перемещения сечений по направлению оси x .

Рис. 1.35	Рис. 1.36	Рис. 1.37
Задача 1.16. Упругий стержень AK жесткостью EF жестко за-
делан верхним сечением. Между нижним сечением		K и поверхно-
стью B − B имеется зазор	<< a (рис. 1.36). Стержень в сечении C

статически нагружается силой до величины P , при достижении которой сечение K коснется поверхности B − B . В момент касания сечение K приваривается к поверхности B − B , после чего стержень разгружают. Определить остаточные напряжения в стержне.

Задача 1.17. Для стержня AB , защемлённого крайними сечениями (рис. 1.37), построить эпюры напряжений σx по длине и пе-

ремещений ux сечений, вызванных действием собственного веса.

γ, F, l, Eсж = 2Eраст известны.

1.6.Решения, указания, ответы

1.1. График имеет вид:

55

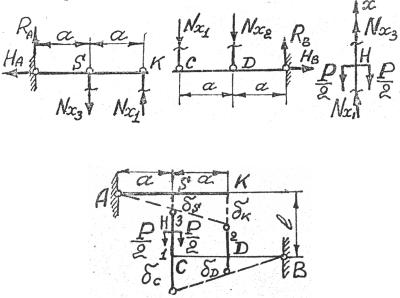
1.2. 1. Определяем тип задачи по формуле (1.13): S = 3 2 −6 = 0 , так как K = 2 , Ш = 6 , т.е. задача статически определимая.

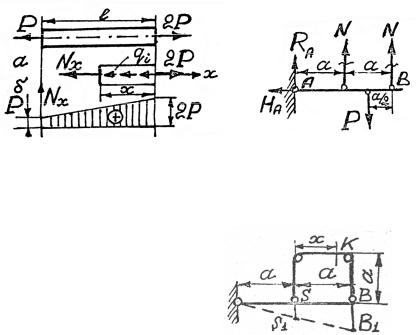
2.Выделяем объекты равновесия (рис. 1.38).

3.Составляем уравнения равновесия для первой, второй и третьей

схемы рис. 1.38:

∑mA = 0 ; ∑mB = 0 ;

∑x = 0 ;

откуда

Nx

= −1 P

1

3

(нужно поменять направление Nx

на обратное, т.е. в стержне имеет

1

месторастяжение), Nx

= 2 P (сжатие) ,

Nx

=

4 P (растяжение) .

2

3

3

3

4. Определяем перемещения и деформации (рис. 1.39). δC > δS , так

какстержни1 и3 растягиваются, т.е. δC −δS =

l1 +

l3 ;

δK > δD , так

Nx

li

как стержень 2 сжимается,

т.е. δ

K

−δ

D

=

l

.

l

=

i

. С уче-

2

i

EF

том, что δK =

2a

,

δC

=

2a

, найдем, что δS =

13

Pl

.

δS

a

δD

a

9 EF

Рис. 1.38

Рис. 1.39

56

5. Определяем работу силы P и потенциальную энергию де-

формации.

Работа

A =

1

P u

н

=

1

P (δ

S

+

l ) =

25 P2l

,

где

2

2

18 EF

3

uH = δS +

l3 – перемещение точки приложения силы, т.е.

путь,

пройденный силой. Потенциальная энергия деформации стержне-

Nx2

l1

Nx2

l2

Nx2

l3

25 P2l

вой системы U =

1

+

2

+

3

=

.

2EF

2EF

2EF

18 EF

1.3. 1. Сила, вызывающая ускорение,

равна 2P − P = P ; ускоре-

ние a = P / m ; интенсивность распределенной по длине силы инер-

ции qi = ma / l .

2. Исходя из принципа Даламбера, составим уравнение равновесия для части стержня длиной х (рис. 1.40, а): −Nx −qi x + 2P = 0 ,

откуда Nx = 2P − qi x . При x = 0 Nx = 2P , при x = l	Nx = P
(рис. 1.40, б).

Рис. 1.40	Рис. 1.41

1.4. 1. Выделяем объект равновесия с учетом того, что во всех участках троса Nx = N – растягивающие (рис. 1.41).

Рис. 1.42

57

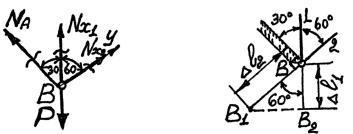
2.Из уравнения равновесия ∑mA = 0 N = P2 .

3.Рассмотрим деформированную систему (рис. 1.42). Пусть се-

чение K неподвижно, тогда отрезок SS =

SK

=

N (a + x)

, отрезок

1

EF

N (a + a − x)

BB

=

BK

=

,

а

так

как

SS1

=

SK

=

1

EF

BB1

BK

=

N (a + x) EF

=

a

, то 2a − x = 2a + x

x = 0 .

EF N (a + a − x)

2a

4. Проверяем

SK =

N a

;

BK =

N 2a

SK

=

a

.

EF

EF

BK

2a

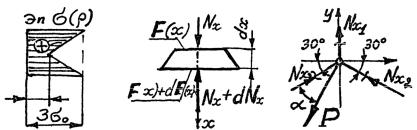
1.5. 1. Выделяем объект равновесия (рис. 1.43).

2. Составляем уравнение равновесия в виде суммы проекций сил на ось, проведенную так, чтобы в уравнение вошли только интересующие нас силы в упругих элементах (т.е. на ось, перпендикуляр-

ную к AB ), ∑y=0 : −Psin 30+Nx2 +Nx1 sin 30= 0 .

Рис. 1.43 Рис. 1.44

3. Строим диаграмму перемещений для узла B (рис. 1.44). l1 = l ,

l2 = l / sin 30 ,			B1	– новое	положение узла				B ,	BB 1= l2 ,
		Nx	l1
BB =	l =	1		= 0,08 см	N	x	=16	кН.
2	1	EF
						1
4. Из диаграммы перемещений							l1 =	l2 sin 30	Nx	= Nx .
									1	2
					58

5. Подставляя значения Nxi в уравнение п.2, найдем: P = 48 кН.

1.6. Вариант 1. Так как справедлива гипотеза плоских сечений, т.е. ε =const, то эпюра σx (ρ) согласно закону Гука σx (ρ) = ε E(ρ) будет иметь вид, представленный на рис. 1.45.

Вариант 2. Для случая, если необходимо указать значения σx на эпюре, выраженные через заданные P и r .

1. Из эпюры E (ρ) следует, что E (ρ)= E 1

+

2ρ

.

r

2. σx (ρ) = ε E (ρ) . Тогда

P = ∫σx (ρ) dF =

7

π ε E r2

(где

3

3P

F

3P

2ρ .

dF =2πρ dρ), откуда

ε =

,

σx (ρ)=

1

+

При

7πE r2

7π r2

r

ρ = 0 σx (ρ)= σ0 =

3P

; при ρ= r σx (r) = 3σ0 =

9P

.

7πr2

7πr2

Рис. 1.45 Рис. 1.46 Рис. 1.47

1.7. 1. Воспользуемся методом сечений и выделим элемент на расстоянии x от верхнего сечения, высотой dx (рис. 1.45).

	2. ∑x = 0 : Nx −(Nx + dNx )+ γ F (x) dx = 0 , откуда		dNx =
	= γF (x) dx =[σ] dF (x), так как в любой точке σx =	dNx	=[σ] .
		dF (x)

59

3. Разделив переменные				и	проинтегрировав,	P	получим
ln F (x)=	γ		x +C . Так как	при	x = 0 F (x)= F 0=			, тогда
	[σ]
						[σ]

γx

F (x)= F 0 e[σ] .

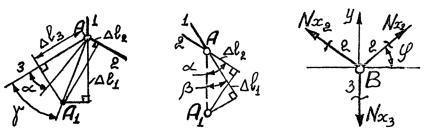
1.8. 1. Под действием силы P усилия Nx возникают только в стержнях, прикрепленных к узлу А (рис. 1.47). Уравнения равновесия запишем в виде ∑z = 0 , ∑y = 0 . Задача один раз статически

неопределимая.

2. Изобразим диаграмму перемещений (рис. 1.48). При ее построении выдержано условие строгого соответствия силовой схемы и деформированной системы.

		3.	Составим			дополнительные уравнения AA1 =		l1	=
								cos(β− γ)
	=		l2	=		l3	. Из дополнительных уравнений найдем угол γ ,
		cos(2β− γ)			cos γ

значения которого сравним с углом α , полученным из уравнения равновесия п.1. Доказательством послужат равенства этих углов.

Рис. 1.48 Рис. 1.49 Рис. 1.50

1.9. Из условия следует, что изменение длины стержней зависит

только от температуры, т.е. l = α	t li . Построим диаграмму пе-
ремещений шарнира А (рис. 1.49).	А1 – новое положение шарнира

60