Исаченко Сопротивление материалов ч.1 2010

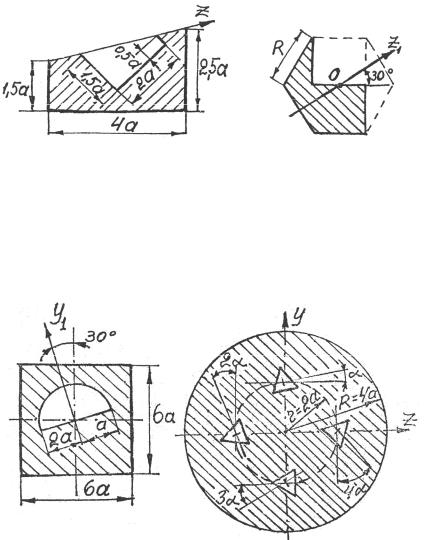
Рис. 3.34

Рис. 3.35

Задача 3.15. Найти осевой момент инерции Iz1 заштрихованной

площади (рис. 3.35), представляющей собой часть правильного шестиугольника со стороной R.

Задача 3.16. Определить момент инерции относительно оси y1 для плоской фигуры (рис. 3.36).

Рис. 3.36

Рис. 3.37

Задача 3.17. Найти момент инерции относительно оси z плоской фигуры (рис. 3.37), если сторона равносторонних треугольников-

111

вырезов равна a. Центры тяжести треугольников лежат на окружности радиуса r = 2a , угол α =10° .

Задача 3.18. Фигура (рис. 3.38) образована n вписанными друг в друга квадратами ( n → ∞ ). Вычислить момент инерции относительно оси z1 .

Задача 3.19. При каком значении h все оси, проходящие через точку А трапеции (рис. 3.39), будут главными?

Рис. 3.38

Рис. 3.39

Задача 3.20. Установить, при каком значении а оси z, y будут главными осями сечения (рис. 3.40).

Рис. 3.40

112

Задача 3.21. Для фигуры, вписанной в окружность радиусом R, образованную двумя диаметрами AF и CD и хордами AE, EC, FK, KD (рис. 3.41), определить угол α, при котором Iz = I y .

Рис. 3.41 Рис. 3.42

Задача 3.22. Для плоской фигуры (рис. 3.42) определить на оси y положение точки, через которую главные оси проходят под углом 45° к оси y.

Задача 3.23. При каком соотношении h / b момент инерции и момент сопротивления относительно оси z будут максимальными для плоской фигуры (рис. 3.43).

Рис. 3.43

Рис. 3.44

113

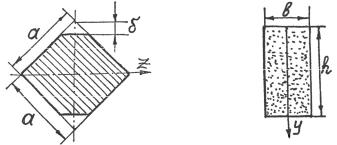
Задача 3.24. Как обтесать круглое бревно, чтобы полученный из него брусок прямоугольного поперечного сечения обладал наибольшей прочностью при изгибе (рис. 3.44).

Задача3.25. Найти, при каком значении δ момент сопротивления относительно оси z поперечного сечения балки (рис. 3.45) будет наибольшим. Насколькоповыситсяпрочностьбалкиприоптимальном δ?

Рис. 3.45	Рис. 3.46

Задача 3.26. Стержень прямоугольного сечения (рис. 3.46) сделан из пористого материала. Плотность пор меняется по высоте сечения по закону ρ( y) = ρ0 y / h , где ρ0 = const . В целом поры ос-

лабляют сечение на 25 %. Определить момент инерции сечения относительно его центральной горизонтальной оси.

		3.3. Решения, указания, ответы
	3.1. При z = l	y(l) = h = aln , откуда a =						h	(рис. 3.47). Площадь
								ln
			l
						h l
	фигуры F = ∫dF = ∫ ydz = ∫			h	zndz =		.		Статический момент
	F	F	0 ln			n +1

площади относительно оси y найдем по формуле (3.2):

		l	h		n+1		hl2
Sy = ∫ z dF = ∫ zy dz = ∫				z		dz =		.
							n + 2
F	F	0 ln

114

Рис. 3.47

Абсциссу центра тяжести фигуры определим по формуле (3.6):

zc =

Sy

=

n +1

l

1

F

n + 2

тогда l − zc =

l .

n

+ 2

Если

n =1 ,

т.е. фигура представляет собой треугольник, то

F =

1

hl ,

Sy =

hl2

, zc =

2

l , l

− zc

=

1

l .

2

3

3

3

Если n = 2 , т.е. фигура сверху ограничена квадратичной параболой, то

	F =	1	hl ,	Sy =	hl2		zc =	3	l , l − zc =	1	l .
						,
		3			4			4		5

Если n = 3 , т.е. фигура сверху ограничена кубической парабо-

	лой, то F =	1	hl ,	S y =	hl 2	,	zc =	4	l , l − zc =	1	l .
		4			5			5		5

3.2. Для того чтобы центр тяжести находился на прямой АВ, последняя должна совпадать с центральной осью zc .

Согласно положению 3.1.1 статический момент всей площади фигуры Szc = SAB должен быть равен нулю.

Следовательно, для фигуры (рис. 3.48), состоящей из двух час-

тей

1

и 2: S

= F y

+ F y

=

πR2

4 R

+ 2Rh

−

h

= 0

, откуда

z

c

c

c

1

2

3 π

1

2

2

2

h =

2

R .

6

115

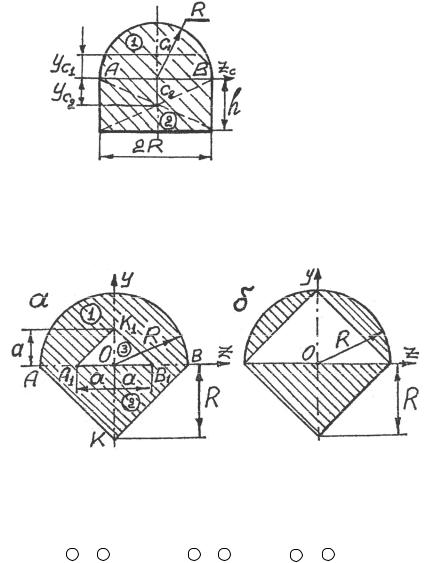
Рис. 3.48

3.3. Представим всю фигуру, состоящую из трех частей, в алгебраическом смысле: 1-я – полукруг; 2-я – треугольник ABK; 3-я – треугольник A1B1K1 (рис. 3.49, а).

Рис. 3.49

Для каждой из фигур моменты инерции относительно осей z, y, проходящих через точку O, равны между собой:

Iz1 = I y1 =	1 πR4		;	Iz2 = I y2 =	R4	;	Iz3 = I y3 =	a4	.
	2	4			6
							6

Следовательно, для всей фигуры оси z, y являются главными, так как y – ось симметрии, и моменты инерции для всей фигуры относительно этих осей равны, т.е. Iz = I y .

116

Для того чтобы эти оси были бы главными и центральными, необходимо, чтобы центр тяжести всей фигуры совпадал с точкой О.

Это условие будет выполняться, если статический момент площади всей фигуры относительно оси z будет равен нулю:

1	2	3		1		2	4 R				1			2			1			1		2	1
Sz = Sz	+ Sz	− Sz	=		πR					+		2R				−		R	−		2a			a = 0	,
				2			3 π				2						3			2			3
откуда a = R ,
		т.е. фигура					должна						иметь					вид,			показанный на

рис. 3.49, б.

Главные центральные моменты инерции будут равны моментам инерции относительно осей z и y для полукруга:

Iz = I y = πR8 4 .

3.4. Учитывая свойство аддитивности геометрических характеристик, для фигуры рис. 3.24, а моменты инерции

Iz = I y = πR4 4 − π4r4 = π4 (R4 − r4 ) .

Для фигуры рис. 3.24, б, учитывая положение 3.1.4, найдем

Iz = π4 (R4 −r4 ) ,

а для определения I y воспользуемся формулой (3.9):

I y =	1 π		(R	4	− r	4		1 π			(R	4	− r		4	) +(R + r)		2	1			πR	2			1	πr	2
							) +																		−				.
	2 4																									2
								2 4											2
3.5. Из вершин А и D треугольника (рис. 3.50) опустим перпен-
дикуляры на медиану и ее продолжение. Из рисунка имеем
		H = b sin α ,						B =			h			,		Iz = 2	BH 3		=		hb3			sin2			α .
											sin α
				2												12						48

3.6. Решение основано на положении 3.1.4, формуле (3.26) и (3.9). Центр тяжести фигуры лежит на высоте 3b от основания фигуры (см. рис. 3.26). Относительно горизонтальной оси zc , проходя-

щей через центр тяжести I	zc	=	BH 3	= 72b4 , так как B = 4b ,
		12
H = 6b .

Iz = Izc + a2F = 72b4 +b2 4b 6b = 96b4 .

117

Рис. 3.50

3.7. Для решения задачи воспользуемся формулами (3.8) и (3.35):

	πR	4	R
I p = Iz + I y = 2Iz =			− n ∫2	ρ2 (αρ dρ) , где αρ dρ = dF – элемен-
	2		R1

тарная площадка выреза (см. рис. 3.27).

Проведя интегрирование второго члена выражения для I p , по-

лучим I		=	1		πR4	− nα	65		R4
	z									.
			2		2		1024

3.8. Моменты инерции квадрата с вырезом (см. рис. 3.28) отно-

сительно любой центральной оси Iz		= I y =	a4	−	(na)4	= I y .
			12		12
	c	c

Для определения момента инерции относительно оси z восполь-

Iz =

a4

(na)4

a 2

a2

−(na)2 .

зуемся формулой

(3.9):

−

+

12

12

2

Учитывая, что Iz = 5Iy , найдем n =

1

.

2

3.9. Из рис. 3.51

имеем, что

h = R

3

.

Используя

формулы

2

(3.29) и (3.30), получим, что

Iz = I y = 4

Rh3

+ 2

Rh3

=

5 3

R4

=

0,5413R4 ,

16

12

4

118

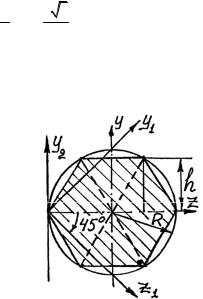
F = 6 12 Rh = 323 R2 = 2,598R2 .

Эти же значения можно взять из [17]. Для определения I y2 вос-

пользуемся формулой (3.9): I y2 = I y + R2 F = 3,1393R4 .

Рис. 3.51

Так как оси

z,

y2 –

главные, то

Izy2 = 0 , тогда по формуле

(3.15) найдем

Iz − I y2

Iz y

−2,598R4

4

=

sin 2α =

(−1) =1,3R

,

2

2

1 1

так как α = −45°, sin 2α = −1 .

3.10. Вариант 1. Достроив фигуру

(рис.

3.52)

до

параллело-

грамма, найдем по формуле (3.26)

Iz =

1 BH 3

=

1

6b(4b)3

=16b4 .

2

12

Вариант 2. Центральная ось

2

12

zc расположена

на

расстоянии

1 H = 4 b

от

оси

z ,

тогда

расстояние

от

оси

z до z

3

3

1

c

a = 2b − 4 b =

2

b .

3

3

119

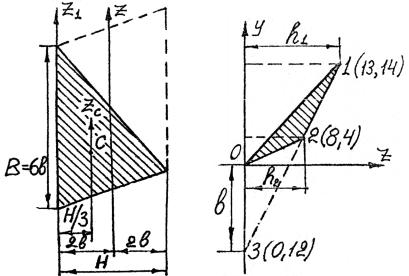
Рис. 3.52

Рис. 3.53

Воспользовавшись формулами (3.28) и (3.9), найдем

	BH	3	+ a2 F =	6b(4b)3 2			2	1	6b 4b =16b4 .
Iz =					+		b
	36			36		3		2

В варианте 2 решение более сложное, чем в варианте 1.

3.11. Продлив прямую 1 – 2 (рис. 3.53) до пересечения с осью y, получим точку 3, координаты которой найдем из уравнения прямой

y − y1	=	z − z1	. Из последнего уравнения z = 0 ,	y = −12 см, т.е.
y2 − y1		3		3
		z2 − z1

b =12 см, h1 =13 см, h2 =8 см.

Момент инерции относительно оси y треугольника 012 найдем как разность моментов инерции для двух треугольников:

		bh3		bh3
	Iz =	1	−	2	.
		12		12

3.12. Разбив всю фигуру на две части (см. пунктир на рис. 3.54 фигуры), замечаем, что она состоит из двух одинаковых уголков,

120