Исаченко Сопротивление материалов ч.1 2010

VI операция. Определение перемещений заданных сечений.

Прогиб сечения С найдем, подставив в (5.10) значения θ0 и y0 , а

также x = 2l ; получим yC =

5 ql 4

= 0,61 10−2 м.

24 EJ z

Продифференцируем уравнение (5.10), тогда

EJ z

dy

= EJ zθ = EJ z θ0

q(x − 0)

3

RB (x −l)2

q(x − l)3

−

+

+

−

dx

3!

2!

3!

x>l

−

P(x − 2l)2

.

(5.11)

2!

x>2l

Угол поворота сечения D найдем, подставив в (5.11) значение x = 3l :

θD = − 18 ql3 = −0,011 рад = −0,63°. 24 EJ z

VII операция. Изображение изогнутой оси балки. Изогнутую ось удобно строить на эпюре изгибающего момента M z , так как

знак эпюры M z указывает на то, какие волокна балки сжаты, а какие растянуты. Согласно принятому правилу знаков эпюра M z

всегда «располагается» на сжатых волокнах.

Изогнутая ось заданной балки изображена штриховой линией на рис. 5.5, в, при этом масштаб искажен в сторону большого увеличения прогибов и углов поворота сечений.

Примечание. Решение задачи может быть упрощено, если расположить начало координат на опоре D (ось х направить справа налево). В этом случае не нужно будет догружать балку дополнительной и компенсирующей нагрузкой; начальный параметр y0 = 0 . При этом нужно помнить, что правило знаков для угла поворота

θ меняется на противоположное, т.е. при θ > 0 сечение поворачивается от своего первоначального положения по часовой стрелке, а при θ < 0 – против часовой стрелки, что справедливо и для метода непосредственного интегрирования дифференциальных уравнений изогнутой оси.

П р и м е р 3

Определить стрелу прогиба для консольной балки (рис. 5.6).

221

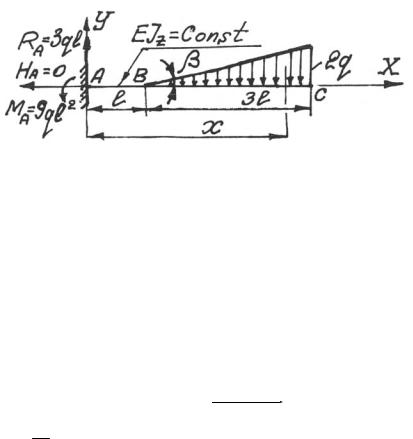
Рис. 5.6

I операция. Изображение расчетной схемы (см. рис. 5.6)

II операция. Определение опорных реакций. Используя урав-

нения равновесия в виде ∑X = 0 ; ∑Y = 0 ; ∑mA = 0 , найдем,

что H A = 0 ; RA = 3ql , M A = 9ql 2 .

Для проверки можно воспользоваться уравнением ∑mB = 0 .

III операция. Составление универсального уравнения:

EJ z y = EJ z y0

+ EJ z θ0

x1

−

M A (x − 0)

2

+

1!

2!

RA (x − 0)3

tg β(x − l)5

+

−

,

(5.12)

5!

3!

x>l

tg β = 23ql .

IV операция. Определение начальных параметров. Располо-

жение начала координат в заделке определяет, что y0 = 0 и θ0 = 0 .

	V операция. Определение прогиба		yC . Подставляя в (5.12)
	значения y0 , θ0 и x = 4l , найдем, что
	yC = f = −	41,3ql 4	.
		EJ z

П р и м е р 4

Определить стрелу прогиба в консольной балке (рис. 5.7, а).

222

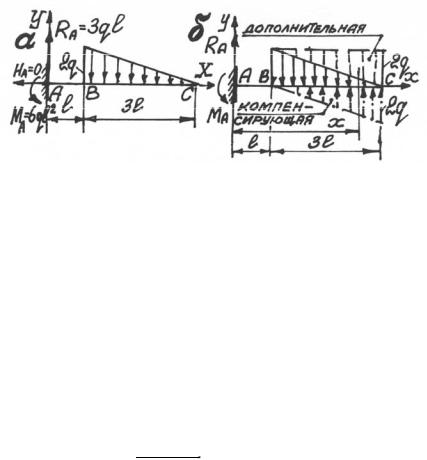
Рис. 5.7

I операция. Изображение расчетной схемы (см. рис. 5.7, а). II операция. Определение опорных реакций. Используя урав-

нения равновесия в виде ∑X = 0 , ∑Y = 0 , ∑mA = 0 , найдем,

что H A = 0 , RA = 3ql , M A = 6ql 2 .

Для проверки можно воспользоваться уравнением ∑mB = 0 .

III операция. Составление расчетной схемы с учетом правил метода начальных параметров (рис. 5.7, б).

IV операция. Составление универсального уравнения:

EJ z y = EJ z y0 + EJ z θ0 x

−

M A (x − 0)2

+

RA (x − 0)

3

−

2!

3!

−

2q(x − l)4

+

tg β(x − l)5

,

(5.13)

4!

5!

2q

x>l

где

tg β =

.

3l

Vоперация. Определение начальных параметров. y0 = 0 и

θ0 = 0 , что является следствием расположения начала координат в

заделке.

VI операция. Определение прогиба сечения С. Подставляя в

(5.13) значения y0 , θ0 и x = 4l , найдем, что

223

yC = f = −	21,4ql 4
		.
	EJ z

П р и м е р 5

Для консольной балки AD (рис. 5.8, а) определить прогиб сечения D и угол поворота сечения С.

Рис. 5.8

I операция. Изображение расчетной схемы (см. рис. 5.8, а). II операция. Определение опорных реакций. Используя урав-

нения равновесия в виде ∑X = 0 , ∑Y = 0 , ∑mA = 0 , найдем,

что H A = 0 , RA =12ql , M A = 60ql 2 .

Для проверки можно воспользоваться уравнением ∑mC = 0 .

III операция. Составление расчетной схемы с учетом правил метода начальных параметров (рис. 5.8, б).

IV операция. Составление универсального уравнения:

EJ z y = EJ z y0 + EJ z θ0 x −

M A

(x − 0)

2

+

RA

(x − 0)

3

−

2!

3!

tg β(x − l)5

4q(x − 7l)4

tg β(x − 7l)5

−

+

+

,

(5.14)

5!

4!

5!

2q

x>l

x>7l

где

tg β =

.

3l

224

Vоперация. Определение начальных параметров. y0 = 0 и

θ0 = 0 , что является следствием расположения начала координат в

заделке.

VI операция. Определение искомых перемещений. Прогиб сечения D найдем, подставив в (5.14) значения y0 , θ0 и x =10l :

yD = f

= −

1313,2ql 4

.

EJ z

Для определения θC продифференцируем уравнение (5.14), в

результате получим

EJ z y′ = EJ z θ = −M A x +

RA

x2

tg β(x − l)4

4q(x −

7l)3

−

+

+

2

24

6

tg β(x − 7l)4

x>l

x>7l

+

.

(5.15)

24

Подставляя в (5.15) x = 7l , найдем, что

θC = −

164 q l3

.

EJ z

5.4. Интеграл Мора

Интеграл Мора для определения перемещений при изгибе, пренебрегая влиянием поперечной силы, имеет вид

		M z			z dx
	δ = ∫		M			,	(5.16)
		EJ		z
	L

где δ – перемещение (прогиб или угол поворота), M z – значение

изгибающего момента в текущем сечении силового участка от заданных нагрузок или, как принято говорить, от грузового состояния балки (сами моменты M z при этом называют грузовыми мо-

ментами, а эпюру M z – грузовой эпюрой), M z – значение изги-

бающего момента в том же текущем сечении от единичного усилия, но приложенного в том сечении, перемещение которого опре-

225

деляется, и по тому направлению, по которому определяется перемещение.

Если определяется прогиб, т.е. δ = y , то единичное усилие пред-

ставляет собой сосредоточенную силу P0 =1, а если определяется угол поворота, т.е. δ = θ, то единичное усилие представляет собой

сосредоточенный момент M 0 =1 .

Предел интегрирования L в формуле (5.16) указывает на то, что интегрирование должно быть произведено по всей длине балки.

Полученное в результате интегрирования значение δ со знаком «+» (плюс) говорит о том, что перемещение δ совпадает с направлением единичного усилия, и, наоборот, знак «–» (минус) свидетельствует о том, что перемещение δ направлено в сторону, противоположную направлению единичного усилия.

Порядок определения перемещений с помощью интеграла Мора рассмотрим на конкретном примере.

П р и м е р 6

Определить для балки (рис. 5.9, а) постоянной жесткости прогибы в сечениях С и D и углы поворотов сечений А и D.

Iоперация. Изображение расчетной схемы (см. рис. 5.9, а). II операция. Определение опорных реакций. Используя урав-

нения равновесия в виде ∑X = 0 , ∑mB = 0 , ∑mA = 0 , найдем,

что H A = 0 , RA = 54 qa , RB = 34 qa .

Для проверки можно воспользоваться уравнением вида

∑Y = 0 .

III операция. Наметим абсциссы xi текущих сечений для каж-

дого силового участка балки, при этом будем стремиться к тому, чтобы в выражении для изгибающих моментов входило как можно меньше членов. Начало абсцисс xi будем устанавливать не в ка-

ком-либо одном, раз выбранном сечении, а от начала каждого силового участка, что определит во всех интегралах нижний предел, равный нулю (см. абсциссы xi на рис. 5.9, а). Итак, 0 ≤ x1 ≤ a ,

0 ≤ x2 ≤ a , 0 ≤ x3 ≤ a , не забывая, что изгибающий момент в сече-

226

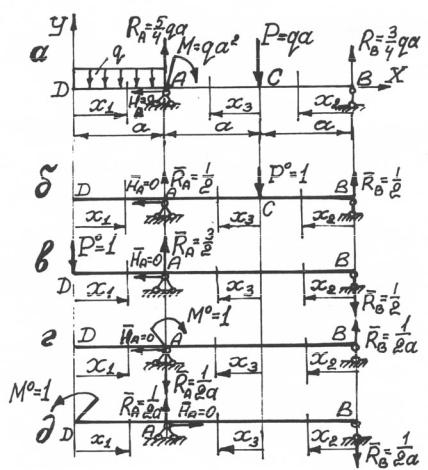
нии равен алгебраической сумме моментов всех сил, лежащих по одну сторону от сечения (см. значение M z в IV операции).

Рис. 5.9

IV операция. Определение изгибающих моментов M z в те-

кущих сечениях каждого силового участка:

		qx2
	M z = −	1	, M z		= RB x2 ,	M z		= RB (a + x3 ) − P x3 .
		2		2			3
	1

227

(О правиле знаков для изгибающих моментов см. с. 166 – 168.)

V операция. Изображение единичной системы. Единичной системой будем называть схему балки, загруженную только (!) единичным усилием в соответствующем сечении по искомому направлению.

Для определения yC единичная система представлена на рис. 5.9, б, для определения yD – на рис. 5.9, в, для определения θA – на рис. 5.9, г, для определения θD – на рис. 5.9, д.

Для каждой единичной системы повторяем те же операции II, III, IV, что и для балки, загруженной заданными усилиями.

На схемах единичных систем показаны реакции опор, те же абсциссы текущих сечений, что и на рис. 5.9, а.

Изгибающие моменты для единичных систем будут равны:

для схемы рис. 5.9, б (определение прогиба yC ):

= 0 ,

=

B x2 ,

z

=

B (a + x3 ) − P0 x3 ;

M

z

M

z

2

R

M

R

1

3

для схемы рис. 5.9, в (определение прогиба yD ):

= −P0 x ,

= −

x

,

= −

(a + x

) ;

M

z

M

z

R

B

2

M

z

R

B

3

1

2

3

1

для схемы рис. 5.9, г (определение угла поворота θA ):

z = 0 ,

z

=

B x2 ,

z =

B (a + x3 ) ;

M

M

2

R

M

R

1

3

для схемы рис. 5.9, д (определение угла поворота θD ):

z

= −M 0 ,

z

= −

B x2

,

z

= −

B (a + x3 ) .

M

M

2

R

M

R

1

3

VI операция. Последняя. Запись интегралов Мора, проведение интегрирования и получение значений перемещений

				1		a			3							1		a		3
	yC =					∫						qax2					x2 dx + ∫							qa(a + x3 ) − qax3												×
									4							2
				EJ z														0		4
						0
							1																				7 qa4
					×						(a + x3 ) −1							x3 dx					=								,
																											24 EJ z
							2
				1	a						qx		2						a		3											1
															(− x			)dx +
y		=						−				1														qa x					−		x		dx +
	D		EJ z ∫									2							∫				4									2
																	1									1				2				2
					0														0

228

	a	3				1				11		qa	4
	+ ∫
				qa(a + x3 ) − qa x3	−		(a + x3 ) dx		= −					,
			4			2				24 EJ z
	0

где знак «–» (минус) в результате говорит о том, что балка в сечении D прогибается вверх, в сторону противоположную направле-

нию P0 =1, приложенном в сечении D.

	1	a	3			1				a	3
θA =		∫			qax2			x2	dx + ∫				qa(a + x3 ) − qax3	×
				4			2a					4
	EJ z									0
		0

θD =

+a∫ 3

0 4

1

14 qa3

×

(a + x3 ) dx

=

,

2a

24 EJ z

a

qx

2

a

3

1

1

(−1)dx

−

1

+

qax

−

x

dx +

EJ z ∫

2

∫

4

2a

2

2

0

0

1

10 qa3

qa(a + x3 ) − qax3

−

(a + x3 ) dx = −

,

2a

24 EJ z

где знак «–» (минус) в результате свидетельствует о том, что угловое перемещение θD направлено в сторону, противоположную на-

правлению момента M 0 =1 , т.е. по часовой стрелке.

В выражении для yC и θA не проводится интегрирование по

первому силовому участку, так как при наличии грузового момента, отличного от нуля на этом участке, момент от единичного уси-

лия M z1 = 0 .

5.5. Способ Верещагина

Способ (правило) Верещагина представляет собой графоаналитическое решение интеграла Мора. Согласно этому способу перемещение

	ω		C	,
δ =		M			(5.17)
	EJ z
где ω – грузовая площадь, т.е. площадь эпюры M z					от заданных

нагрузок; M C – ордината эпюры изгибающего момента от единич-

229

ного усилия под центром тяжести грузовой площади ω. Единичное усилие, как и при определении перемещений с помощью интеграла Мора, приложено в том сечении, перемещение которого находится, и по тому направлению, по которому определяется перемещение.

Операция в числителе формулы Верещагина (5.17) получила название «перемножение» эпюр.

Способ Верещагина допускает «перемножение» эпюр только в том случае, если одна из «перемножаемых» эпюр ограничена прямой неломаной линией, а такими эпюрами как раз и являются эпюры от единичных усилий.

Определение M С не представляет труда. Затруднения возникают при определении положения центра тяжести грузовых площадей ω. Для решения этой задачи воспользуемся следующими рекомендациями.

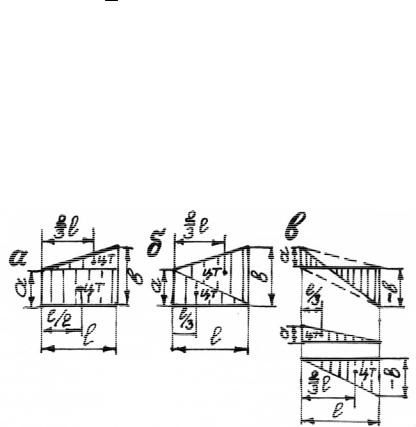
Сложную грузовую эпюру M z следует разбить на простые фи-

гуры, для каждой из которых легко определить абсциссу центра тяжести. При этом площадь каждой простой фигуры умножают на ординату единичной эпюры под ее, простой фигуры, центром тяжести. На рис. 5.10, а, б показаны два варианта разбиения трапеции на простые фигуры, а на рис. 5.10, в – преобразование «перекрученной» трапеции.

Рис. 5.10

230