Исаченко Сопротивление материалов ч.1 2010

А должна быть горизонтальной, так как βA = 0 , чем и определяется выпуклость вверх кривой на эпюре M z на участке АВ.

Для балки (см. рис. 4.16) на участке ВС для M z имеем квадра-

тичную					зависимость. В сечении			с	абсциссой x20 =1,5a
Qy	2	=	dM z			= tgβx	= 0 , следовательно,	βx		= 0 , т.е. в этом сече-
				dx	20			20

нии имеем только одну горизонтальную касательную к кривой функции M z , что и определяет выпуклость кривой на этом участ-

ке. Аналогичные рассуждения можно привести и для участка CD на рис. 4.11, в.

Рассмотрим применение данного приема определения кривизны для участка ВС эпюры M z на рис. 4.11, в. Эпюру Qy можно раз-

бить на две фигуры: прямоугольник b1b2c1c		и треугольник bb1c .
Если бы эпюра	Qy имела только вид	прямоугольника, т.е.
Qy = 3qa = const ,	то эпюра M z была бы ограничена прямой на-

клонной линией. Кривизну функции M z определяет наличие треугольника bb1c ( Q*y имеет в нем линейную зависимость). Согласно треугольнику bb1c Q*y = 0 в сечении С, т.е. угол наклона касатель-

ной к кривой функции M z в сечении С β*C = 0 , т.е. касательная, параллельная оси х, чем и определяется выпуклость вверх кривой функции M z на этом участке. Конечно, учитывая, что tgβC = Qy = 3qa , касательная будет иметь определенный наклон,

но характер выпуклости вверх сохраняется. Прием, изложенный в этом положении, может быть применен и для определения знака кривизны линий, ограничивающих эпюру Qy , если распределенная

нагрузка q(x) меняется по закону степенной или тригонометриче-

ской функции.

4.3.7Б. Для определения знака кривизны линий, ограничивающих эпюру M z , можно пользоваться и следующими соображениями. Любую непрерывную распределенную нагрузку ( q = const или q = q(x) ) можно представить дискретно, как состоящую из систе-

161

мы сосредоточенных сил, каждая из которой равна Pi = q dx . Тогда, пользуясь положением 4.3.1, согласно которому изломы на эпюре M z всегда направлены в сторону, противоположную направлению действующей силы, на эпюре M z будем получать ломаную линию, острия изломов которой направлены против направления Pi = q dx . В пределе эта ломаная линия дает кривую n порядка. Итак, получаем, что выпуклость линий, ограничивающих эпюру M z , всегда направлена в сторону, противоположную на-

правлению распределенной нагрузки.

4.3.8. Изгибающий момент имеет экстремальное значение в тех сечениях, в которых Qy достигает нулевого значения. При этом

(ось x направлена слева направо!) если Qy меняется с положительной на отрицательную, то M z в этом сечении максимальный (см. рис. 4.11, в, сечение с абсциссой x30 = 3,75a ; рис.4.16, г, сечение с абсциссой x20 =1,5a ), и наоборот, если Qy меняется с отрица-

тельной на положительную, то M z в этом сечении минимальный

(см. рис. 4.15, в, сечение С).

4.3.9. Изгибающий момент в сечении установки промежуточного шарнира всегда равен нулю. Так, в сечении С балки (см. рис. 4.16, г) M z = 0 , в крайних концевых сечениях А и К балки

(см. рис. 4.11), где установлены шарнирные опоры – M z = 0 . Если

в таких сечениях приложен сосредоточенный момент, то изгибающий момент равен этому сосредоточенному моменту.

В сечении жесткой заделки изгибающий момент равен по величине опорному моменту.

4.3.10. На крайних концевых шарнирных опорах и в заделке поперечная сила равна опорной реакции.

4.3.11. На свободном (консольном) конце балки Qy = 0 и M z = 0 , если на консольном конце не приложены сосредоточенная сила или сосредоточенный момент, в противном случае Qy и M z

будут равны соответственно силе и моменту (см. рис. 4.17, б и рис. 4.17, в, сечение К).

4.3.12. В соответствии с принятым правилом знаков для изгибающего момента получается, что положительные ординаты эпю-

162

ры M z откладываются все время на сжатых волокнах балки. Действительно, для сечений x1 , x2 , x3 , x4 , x5 балки (см. рис. 4.11)

изгибающие моменты положительные, т.е. балка гнется вогнутостью вверх, в положительное направление оси у («вода не сливается»!); при этом сжатыми оказываются верхние волокна балки, и положительные ординаты M z откладываются в положительное

направление оси у, т.е. все положительные ординаты находятся над базовой линией – на сжатых волокнах.

На участке АВ, ВС и частично на участке CD балки (см.

рис. 4.15) изгибающий момент отрицательный, кривизна ρ1 < 0 , т.е.

балка гнется выпуклостью вверх («вода сливается»!), сжатыми оказываются нижние волокна, и все отрицательные ординаты M z откладываются вниз от базовой линии – на сжатых волокнах.

Итак, рассматривая базовую линию эпюры M z как балку, за-

ключаем, что согласно принятому правилу знаков для изгибающего момента, эпюра изгибающего момента всегда располагается на сжатых волокнах. Это положение в дальнейшем будет использоваться при изображении изогнутой оси балки, а также для определения знака действующих в балке нормальных напряжений.

4.1.4.Примеры построения эпюр Qy и M z

Пр и м е р 5 (рис. 4.17)

Пользуясь вышеприведенными правилами построения и проверки эпюр Qy и M z , для представленной балки покажем, как

строить эпюры не составляя выражения для внутренних силовых факторов в текущих сечениях с абсциссами xi .

I операция. Составление расчетной схемы (см. рис. 4.17, а). II операция. Определение опорных реакций. Составим урав-

нения равновесия:

∑X = 0 − H A = 0 ;

∑mD = 0 RA 3l − 2P l − 3ql 0,5l + M − P 2l = 0

RA = 2,5ql ;

163

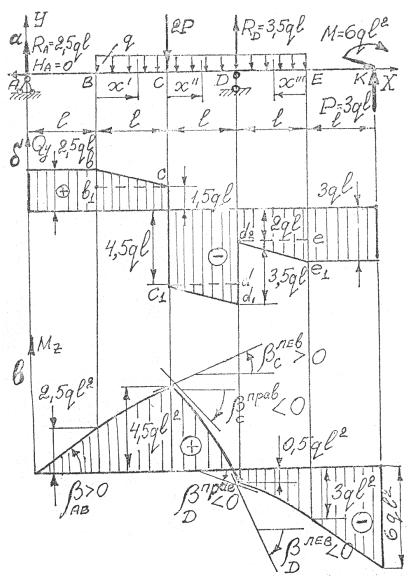
Рис. 4.17

164

∑mA = 0 2P l + 3ql 2,5l − RD 3l + M − P 5l = 0

RD = 3,5ql ;

Проверка:

∑mE = 0 RA 4l − 2P 2l − 3ql 1,5l + RD l + M − P l = 0 , 0 ≡ 0 .

Выносим значения опорных реакций на расчетную схему.

III операция. Построение эпюры Qy . Построение эпюры проведем, определяя только значения Qy в характерных сечениях, т.е.

на границах участков.

На первом этапе будем просматривать балку слева (начиная от сечения А) направо.

1. На опоре А Qy ( A) = RA = 2,5ql (см. положение 4.3.10), со

знаком плюс, так как стремится повернуть лежащую справа часть балки по часовой стрелке.

2.На участке АВ ( q = 0 ) Qy = const = RA = 2,5ql .

3.Начиная с сечения В Qy уменьшается на q x′ , так как q x′

дает отрицательную перерезывающую силу – стремится повернуть против часовой стрелки часть балки, лежащую справа от q x′ , и в

сечении С (слева от сечения!) Qyлев(C) = RA − ql =1,5ql .

4. В сечении С имеет место скачок на величину сосредоточенной силы 2P = 6ql (см. положение 4.3.1) вниз, так как 2P дает от-

рицательную поперечную силу (стремится повернуть справа лежащую часть балки против часовой стрелки). Тогда справа от сечения

Qправy (C) =1,5ql − 6ql = −4,5ql .

5. На участке CD идет дальнейшее уменьшение поперечной силы на величину qx′′ и в сечении D (слева от сечения!)

Qyлев(D) = −4,5ql − ql = −5,5ql . Дальнейшее построение эпюры Qy

проведем, просматривая балку справа (начиная от сечения К) налево. 6. В сечении К Qy (K) = −P = −3ql (см. положение 4.3.11), т.е.

имеет отрицательное значение, так как сила Р стремится повернуть, слева прилежащую часть балки, против часовой стрелки.

165

7.На участке КЕ нет никакой нагрузки и значение перерезывающей силы сохраняется тоже, т.е. Qy = −P = −3ql .

8.Начиная с сечения Е, значение Qy возрастает, так как qx′′′

вызывает положительную поперечную силу – стремится повернуть слева прилежащую часть балки по часовой стрелке, и в сечении D (справа от сечения!) Qправy (D) = −P + ql = −2ql .

Обращаем внимание, что в сечении D получен скачок на величину 5,5ql − 2ql = 3,5ql = RD , что соответствует положению 4.3.1.

IV операция. Построение эпюры M z . Вначале, как и в случае построения эпюры Qy , будем просматривать балку слева направо.

1. НаконцевойшарнирнойопореА M z = 0 (см. положение4.3.9).

2. В сечении В M z (B) = RAl = 2,5ql 2 . Значение M z положительное, так как момент RAl стремится изогнуть часть балки АВ по отношению к сечению В вогнутостью вверх («вода не сливается»!).

	На участке					АВ отсутствует	q = 0 ,	Qy = const , и	следовательно,
	эпюра			M z		ограничена	прямой	наклонной	линией	при
	Qy =	dM z			= tgβ > 0 , т.е. βAB > 0 .
			dx							l
	3. В сечении С изгибающий момент M z (C) = RA 2l − ql										=
										2

= 4,5ql 2 . На участке ВС эпюра M z ограничена кривой второго порядка. Кривая имеет выпуклость вверх, что определяется треугольником bb1c на рис.4.17, б (см. положение 4.3.7А).

4. В сечении D M z (D) = RA 3l − q 2l l − 2P l = −0,5ql 2 . На участке CD эпюра M z ограничена кривой второго порядка с вы-

пуклостью вверх, что определяется треугольником dc1d1 на рис. 4.17, б (см. положение 4.3.7А).

Дальнейшее построение эпюры M z проведем, просматривая балку справа (начиная от сечения К) налево.

166

5. В сечении К M z (K) = −M = −6ql 2 (см. положение 4.3.11).

Изгибающий момент имеет отрицательное значение, так как сосредоточенный момент М стремится изогнуть слева примыкающую к сечению К часть балки выпуклостью вверх («вода сливается»!).

6. В сечении Е M z (E) = −M + P l = −3ql 2 . Эпюра M z на участке КЕ ограничена прямой наклонной линией, так как Qy = 0 на

этом участке.

7. В сечении D M z (D) = −M + P 2l − q l 2l = −0,5ql 2 . На участке ED эпюра M z ограничена кривой второго порядка, так как

Qy на этом участке имеет линейную зависимость. Направление кривизны определяется треугольником ed2e1 (рис. 4.17, б).

Обращаем внимание, что на эпюре M z в сечении В отсутствует

	излом линии, ограничивающей эпюру,			так как действительно в
	этом сечении имеется только одно значение Qy =				dM z	= tgβ, т.е.
					dx
	только один угол β =βAB .	В сечении С имеем две касательные к
	кривой, ограничивающей	эпюру	M z :	βCлев > 0	(соответствует
	Qyлев(C) = tgβ =1,5ql ) и βCправ < 0		(соответствует Qyправ(C) = tgβ =

= −4,5ql ). В сечении D также две касательные, проходящие под

углом	βлевD < 0 (соответствует Qyлев(D) = tgβлевD = −5,5ql < 0 ) и
βправD	< 0 (соответствует Qyправ(D) = tgβправD = −2ql < 0 ).

На рис. 4.17, в изломы линий, ограничивающих эпюру M z , на-

правлены острием в сторону, противоположную направлению действующей в данном сечении сосредоточенной силы, например в сечении А, С, D, K.

П р и м е р 6 (рис. 4.18)

Рассмотрим построение эпюр Qy и M z для балки, загруженной распределенной нагрузкой, меняющейся по линейному закону.

167

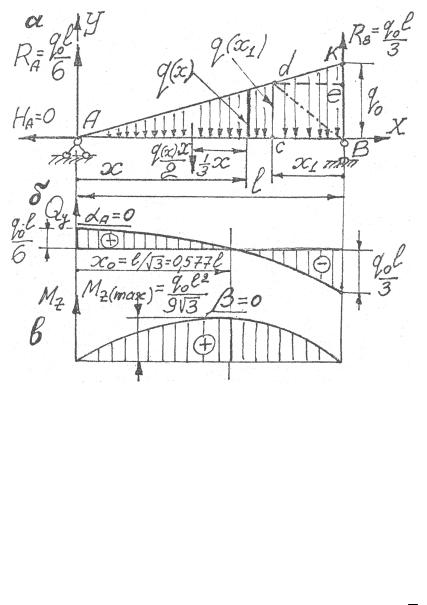
Рис. 4.18

Линию, показывающую закон изменения нагрузки q(x) , назы-

вают грузовой линией, а площадь между грузовой линией и осью балки называют грузовой площадью, величина которой и дает значение равнодействующей данной распределенной нагрузки.

I операция. Составление расчетной схемы (см. рис. 4.18, а). II операция. Определение опорных реакций. Заменяем всю

	распределенную нагрузку ее равнодействующей, равной	1	q0 l
		2

(грузовая площадь равна площади треугольника), которая будет приложена в центре тяжести треугольника, т.е. на расстоянии 23 l

от левого сечения А.

168

Составим уравнения равновесия:

∑X = 0

− H A = 0

;

q0l

∑mB = 0

RA l −

1

q0

l

1

l = 0 ;

RA =

;

2

3

6

∑mA = 0

− RB

l +

1

q0 l

2

l = 0 ;

RB =

q0l

.

2

Проверка:

3

3

1

∑Y = 0

RA −

q0 l + RB = 0 0 ≡ 0 .

2

Выносим значение реакций на расчетную схему.

III операция. Построение эпюры Qy . В сечении х действует

q(x) =

q0

x .

l

2

Qy

= RA −

1

q(x) x =

q0l

−

q0 x

,

2

6

2l

при x = 0

Qy

( A) =

q0l

= RA ,

6

при x = l

Qy

(B) = −

q0l

= −RB .

3

На всей длине l эпюра Qy ограничена параболой. Направление кривизны найдется по положению 4.3.7А в сечении А q = dQdxy =

= tgα = 0 α = 0 , т.е. касательная к эпюре Qy в сечении А долж-

на быть горизонтальна, что и определяет кривизну кривой – выпуклость вверх (см. рис. 4.18, б).

Приравняв уравнение для Qy нулю, получим значение

x0	=	l	= 0,577l , т.е. найдем абсциссу сечения, в котором Qy пе-
	3

реходит через нулевое значение.

Эпюра Qy представлена на рис. 4.18, б.

169

IV операция. Построение эпюры M z . Нагрузку в виде тре-

угольника 12 q(x) x заменяем равнодействующей приложенной в

центре тяжести этого треугольника, т.е. на расстоянии 13 x от рас-

сматриваемого сечения х. Запишем выражение для M z :

M z = RA

x −

q(x) x

1

x =

q0 l

x −

q0 x3

,

2

3

6

6l

при x = 0

M z ( A) = 0 ,

ql 2

x = x0

l

M z (max) =

при

=

,

3

9

3

при x = l

M z (B) = 0 .

Эпюра

M z

ограничена

кривой третьего порядка (см.

рис. 4.18, в).

Кривизна линии,

ограничивающей эпюру M z , опре-

делена, исходя из положения 4.3.7А и 4.3.7Б.

Иногда приходится рассматривать сечения справа (от опоры В) налево, как отмечено на рис. 4.18, а абсциссой x1 (в случае когда балка продолжается влево от сечения А и имеет большое количество нагрузки, что приводит к громоздким выражениям для Qy и

Mz при просмотре балки слева направо).

Вэтом случае пользуются одним из следующих трех приемов. 1-й прием. Нагрузку на длине x1 разбивают на прямоугольную

грузовую площадь

Bcde

и треугольную грузовую площадь edk .

При этом q(x ) =

q0

(l − x ) . Тогда

1

l

1

1

Q

y

= −R

B

+ q(x ) x

+

(q

0

− q(x

)) x

=

1

1

2

1

1

x2

− q

0

l

q

0

=

+ q

0

x −

1

,

3

1

2l

M z = RB x1 − q(x1 ) x1 x21 − 12 (q0 − q(x1 )) x1 23 x1 =

170