Исаченко Сопротивление материалов ч.1 2010

ux2 = ux (B) + Nx2 (x2 −l) . EF

При	x2	= l ux	2	= ux (B) , при x2 = 2l :
		ux (C) = ux (B) +			(−P)l	=	2Pl	и т.д.
					EF		FF

Из второй формулы (1.8) следует, что при действии равномерно распределенной нагрузки, постоянной интенсивностью q на длине l, деформация равна:

l(q) =	ql2
		.	(1.9)
	2EF

При учете собственного веса деформация вертикально расположенного стержня длиной l определится по формуле:

l(γ) =	γl2
		,	(1.10)
	2E

где γ – вес единицы объема или (иначе) удельный вес, Н/м3.

На рис. 1.1, д представлена эпюра перемещений поперечных сечений по направлению оси x . Как видим, эпюра построена в строгом соответствии с дифференциальной зависимостью (1.6), так в сечении В имеем излом, слева от которого угол наклона касательной β > 0 , а справа β < 0 ; в сечении С излом отсутствует, так как здесь

имеем только один угол β < 0 , определяемый единственным значе-

нием εx = EFP < 0 ; в сечении посередине участка CD угол β = 0 .

Работа при упругом деформировании, совершённая при статическом нагружении силой величиной от нуля до P , определяется формулой:

A =	1 P	l =	1 P u ,	(1.11)
	2		2

где u – перемещение точки приложения силы, т.е. путь, пройденный силой при выполнении работы.

Потенциальная энергия деформации, накапливаемая в стержне при упругом деформировании,

		N 2	l		N	2	(x)dx
	U =	x		= ∫		x		.	(1.12)
		2EF			2EF(x)
				l
				11

Потенциальная энергия U численно равна работе A.

Приступая к решению задачи, необходимо ответить на вопрос: является ли рассматриваемая система (задача) статически определимой или статически неопределимой?

Статически неопределимыми системами (задачами) называют-

ся системы (задачи), в которых невозможно определить усилия с помощью одних лишь уравнений статики.

В отличие от статически определимых систем, в элементах которых усилия возникают только от действия внешних нагрузок, в элементах статически неопределимых систем они возникают и при отсутствии внешних сил – в результате изменения температуры системы или ее отдельных элементов, неточности изготовления элементов системы и др.

Степенью статической неопределимости называется разность между числом неизвестных усилий в системе и числом независимых уравнений равновесия, которые можно составить для данной системы. Таким образом, для определения типа данной системы необходимо в расчетной схеме грамотно выделить объекты равновесия и составить для них уравнения равновесия.

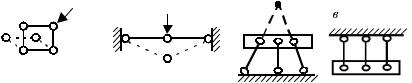
На рис. 1.2 представлены две плоские системы сходящихся сил. Для каждой из них можно составить только два уравнения равновесия, следовательно, число неизвестных в системе а на единицу больше числа уравнений равновесия, поэтому говорят, что такая система (задача) один раз статически неопределимая; в системе б число неизвестных на два превышает число уравнений равновесия – система два раза статически неопределимая.

Для оценки типа системы может быть также рекомендована для многостержневых систем формула:

S = 3K − Ш ,

(1.13)

где S – число избыточных, так называемых «лишних» связей, которое равно степени статической неопределенности; K – число замкнутых независимых контуров в системе в предположении отсутствия шарнирных соединений. Замкнутый контур представляет собой замкнутую цепь, звеньями которой являются стержни, брусья, стержни опорных устройств и земля (пол, стены, потолок), к которой прикреплена система. Независимым называется контур, в котором имеется хотя бы один стержень, не входящий ни в один из остальных контуров. Ш – количество простых шарниров, т.е. шарни-

12

ров, соединяющих два элемента (рис. 1.3). В конструкциях часто встречаются так называемые кратные шарниры (рис. 1.4).

Рис. 1.2

а б в

Рис. 1.3 Рис. 1.4

Число простых шарниров, эквивалентных одному кратному, оп-

ределяется выражением:
Ш = C −1 ,	(1.14)

где С – число стержней (элементов), подходящих к шарниру. Так,

для рис. 1.4, а	число Ш = 4 −1 = 3 , для рис. 1.4, б число
Ш = 3 −1 = 2 , для рис. 1.4, в число Ш = 5 −1 = 4 .
Если S = 0 ,	то имеем статически определимую, геометрически

неизменяемую систему (см. решение задач 1.2, 1.4). Если S > 0 , то

13

имеем статически неопределимую систему (см. решение задач 1.15, 1.18, 1.21, 1.22, 1.23, 1.24). Если S < 0 , то имеем геометрически из-

меняемую систему, т.е. механизм (рис. 1.5).

P	a	P	б

Рис. 1.5

Рис. 1.6

При оценке типа системы следует обращать внимание на то, что система может быть мгновенно изменяемой. Такими системами являются системы, состоящие из двух стержней (рис. 1.6, а), оси которых лежат на одной прямой; элемент, прикреплённый к земле тремя стержнями, оси которых пересекаются в одной точке (рис. 1.6, б), а также система, в которой три стержня параллельны (рис. 1.6, в), оси которых пересекаются в бесконечности. Правильное закрепление в последней системе приведено в задачах 1.10, 1.12.

Для решения статически неопределимых задач используются в основном метод сил и способ совместности перемещений. Оба эти приёма равноправны, но для определённых систем один может дать более простое решение, чем другой.

1.2. Метод сил

Сущность метода сил состоит в переходе от заданной статически неопределимой системы к статически определимой удалением «лишних» связей.

В статически неопределимых системах «лишней» связью называется связь, ответственная за возникновение статической неопределимости. Слово «лишняя» поставлено в кавычки, так как эта связь на практике необходима по конструктивным соображениям, условиям эксплуатации, требованиям прочности и т.д., но может быть удалена без нарушения равновесия и геометрической неизменяемости системы. Эта связь «лишняя» с точки зрения возможности решить задачу методами статики. Число «лишних» связей равно степени статической неопределимости.

14

1.2.1.План решения. Понятие об основной

иэквивалентной системе

Для изображенного бруса (рис. 1.7, а) необходимо определить реакции в заделках A и B, что позволяет найти напряжения на участках AC и CB бруса.

По плану решения методом сил выполняем следующие операции.

1.Составляем расчетную схему (рис. 1.7, б).

2.Проводим анализ схемы. Выбрав на объект равновесия целиком весь брус, составим уравнение равновесия в виде

n
∑Xi = 0 ,	−RA + P − RB = 0 ,	(1.15)

i=1

откуда получаем, что задача один раз статически неопределимая (имеем одно уравнение статики и две неизвестных силы RA и RB ).

3. Выбираем «лишнюю» связь и составляем основную систему. За «лишнюю» связь принимаем, например, заделку правого

крайнего сечения B. Тогда RB будет «лишним» неизвестным.

Основной системой называется статически определимая система, полученная из статически неопределимой путем удаления «лишней» связи (см. рис. 1.7, в).

4. Составляем эквивалентную систему.

Эквивалентной системой называется основная система, загруженная всеми внешними активными силами, в том числе «лишней» неизвестной (см. рис. 1.7, г). Здесь реакция RB переходит в катего-

рию внешних активных сил.

5. Составляем дополнительное уравнение и раскрываем статическую неопределимость.

Для того чтобы эквивалентная система была идентична заданной статическинеопределимой, необходимо, чтобы перемещениесеченияB эквивалентнойсистемыравнялось, какивзаданнойсистеме, нулю, т.е.

UxB = 0 .

Это выражение является дополнительным уравнением в общем виде, с помощьюкоторогораскрываетсястатическаянеопределимостьзадачи.

Исходя из принципа независимости действия сил, можно записать, что

U B =U B (P) +U B (R ) = 0 ,		(1.16)
x x	x B

15

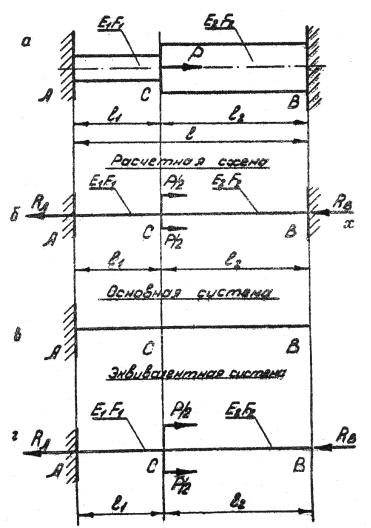
Рис. 1.7

т.е. перемещение сечения B эквивалентной системы складывается из перемещений, вызванных действием внешних активных сил P и RB . Сила P растягивает участок AC бруса, при этом его абсолют-

16

		Nx	l1		Pl
ное удлинение l	(P) =	1		=	1	, так как N	x	= P . На сколько
1		E1F1			E1F1
							1
удлинится участок AC (длина l1 ), на столько переместится вправо,

в положительное направление оси x сечение С, т.е. U С (P) =	l (P) .
x	1

На сколько переместится сечение С, на столько же переместятся и все другие сечения, лежащие справа от сечения С, в том числе и

сечение B. Таким образом, U B (P) =U C (P) = Pl1 . В значении

x x E1F1

UxB (P) удерживается знак «+», так как это перемещение определе-

но положительной (растяжение) деформацией стержня, стержень увеличивает свою длину, удлиняется.

Сила RB сжимает как участок AC, так и участок CB стержня, при этом на сколько сила RB сожмет эти участки, на столько и переместится сечение B влево. Таким образом,

U B (R

) =

l

(R

B

) +

l

2

(R

B

) = −

RBl1

−

RBl2

,

x B

1

E1F1

E2F2

здесь знак «–» поставлен, ввиду того что перемещение определено отрицательной (сжатие) деформацией, стержень уменьшает свою

длину, укорачивается. Особо подчеркнем, что знаки в UxB (P) и

U B (R ) не связаны с направлением оси x!

x B

Подставляя найденные значения U B (P)

и U B (R )

в уравнение

(1.16), получаем

x

x B

U B =

Pl1

− R

l1

+

l2

= 0 ,

E F

E F

E F

x

B

откуда

1 1

1

1

2

2

l1

RB =

,

(1.17)

l1 +l2

E1F1

E

F

2

2

а RA определится из уравнения (1.15):

l2

RA = P − RB = P

.

(1.18)

l

+l

E2 F2

E F

2

1

17

1

1

Дальнейшее решение задачи такое же, как и статически определимой задачи на рис. 1.1, т.е. производим построение эпюр Nx ,

σx , εx , ux . Но после построения эпюры εx следует произвести

генеральную проверку всего предыдущего решения, исходя из следующего соображения. Так как полная деформация всей длины (смещение сечения A по отношению смещения B) равно нулю, то, следовательно,

Ux(полное) = ∫εxdx = 0 ,	(1.19)
L

где εxdx – элементарная площадь, а интеграл по всей длине стержня – площадь всей эпюры εx , следовательно,

=[(ω – ω )/ω ] 100 % = 0.

Здесь ω – суммарная положительная площадь эпюры; ω – суммарная отрицательная. При правильном решении не может превышать 1 % за счет приближенных вычислений.

1.2.2. Влияние монтажного фактора

Как видно из рисунка (рис. 1.8, а), участок BD стержня имеет длину, меньшую чем l3 на величину δ, при этом масштаб δ существенно

отличается от масштаба элементов стержня; δ сопоставимо с деформацией стержня. Найдем реакции в опорах, если деформация участка AC отсилыP l1(P) > δ . Изэтого условияследует, что придействии

силы P правое	крайнее сечение B, перемещаясь	вправо на
UxB (P) =UxC (P) =	l1(P) , упрется в опорную стенку B′	и будет ока-

зывать на нее определенное давление, в результате чего со стороны опорной стены на стержень будет действовать сила реакции RB (см.

рис. 1.8, б), равнаяравнодействующейэтого давления.

Проведем анализ расчетной схемы. Выбрав за объект равновесия весь стержень в целом, составим уравнение равновесия в виде

∑Xi = 0 , т.е.

−RA + P − RB = 0 ,

(1.20)

откуда следует, что задача один раз статически неопределимая.

18

Рис. 1.8

Выбрав за «лишнюю» связь опорную стену B′ , составим основную (см. рис. 1.8, в) и эквивалентную (см. рис. 1.8, г) систему.

19

Дополнительное уравнение получим из следующих соображений. Правое крайнее сечение B стержня заданной системы может переместиться вправо только на величину δ и, следовательно, для того чтобы эквивалентная система была бы идентична заданной, необходимо, чтобы перемещение сечения B эквивалентной системы

Так как

UxB = δ.

(1.21)

U B

=U B (P) +U B

(R ) ,

(1.22)

где

x

x

x

B

Pl1

U B

(P) =U C

(P) =

l (P) =

,

(1.23)

x

x

1

E1F1

а

RBl1

RBl2

RBl3

U B

(R )

= −

−

−

,

(1.24)

x

B

E1F1

E2 F2

E3F3

то, следовательно,

U B

=

Pl1

− R

l1

+

l2

+

l3

= δ ,

(1.25)

E F

E F

x

E F

B

E

F

откуда

1

1

1 1

2

2

3 3

Pl1 −δE1F1

RB =

,

(1.26)

E1F1

l +l

+l

E1F1

2 E F

1

3 E F

тогда изуравнения (1.20)

2

2

3

3

P l

+l

E2 F2

+δE F

2

3 E F

2

2

R

A

= P − R

=

3

3

.

(1.27)

B

l

+l

E2 F2

+l

E2 F2

2

1

E F

3 E F

1

1

3

3

В последнем члене выражения (1.24) –

RBl3

=

l за длину уча-

E3F3

3

стка BD принято l3 ,

l3 −δ ,

а не

что вполне оправдано, так как δ

намного (на несколько порядков) меньше длины l3 и оперировать длиной l3 −δ не имеет смысла. Величина δ соизмерима с переме-

щениями сечений стержня, ввиду чего δ и входит полноправным членом в выражения, например (1.21) и (1.25).

20