Исаченко Сопротивление материалов ч.1 2010

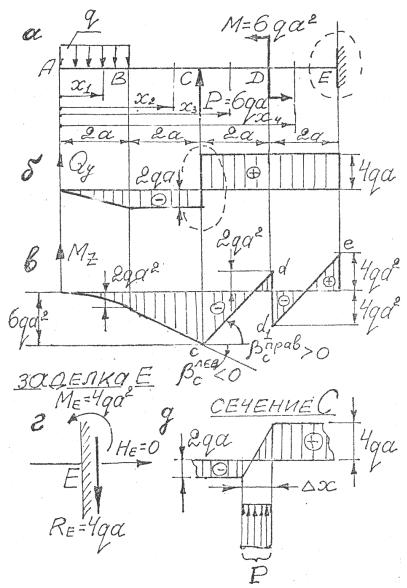
Рис. 4.15

151

Эпюра Qy приведена на рис. 4.15, б.

Формально из эпюры Qy следует, что в сечении С действуют Qy = −2qa и Qy = 4qa . Очевидно, что физически в одном и том же

сечении не могут действовать два разных по величине и знаку внутренних силовых фактора одного смысла. Результат, полученный на эпюре Qy , является следствием схематизации реального

объекта, согласно которой сосредоточенная сила действует в точке, тогда как в действительности сила действует на определенной конечной длине, например, x , и следовательно, действие силы равносильно действию распределенной нагрузки, интенсивностью

q = Px . Таким образом, фактически у сечения С эпюра Qy должна

(без схематизации!) выглядеть так, как показано на рис. 4.15, д. Итак, отвечая на вопрос «чему равна Qy в сечении С», должен

быть дан ответ: подходя к сечению С слева ( x2 = 4a − 0 ) Qy = −2qa , подходя к сечению справа ( x3 = 4a + 0 ) Qy = 4qa .

Аналогичное, по сути, объяснение справедливо и для значения изгибающего момента, например для сечения D балки (см.

рис. 4.15).

IV операция. Составление выражений для M z и построение эпюры M z .

		qx2
M z	= −	1		(квадратная парабола!),
		2
1
	при x1 = 0				M z		= 0 ,
						1
	при x		= 2a		M	z	= −2qa2 ;
		1
M z2	= −2qa(x2 − a)					1
					(линейная зависимость!),
	при x2 = 2a				M z2		= −2qa2 ,
M z	при x2 = 4a				M z2		= −6qa2 ;
	= −2qa(x3 − a) + P(x3 − 4a) (линейная зависимость!),
3
	при x3 = 4a				M z		= −6qa2 ,
						3

152

при x3	= 6a	M z	= 2qa2 ;
		3
M z4 = −2qa(x4 − a) + P(x4 − 4a) − M ,
при x4	= 6a	M z4	= −4qa2 ;
при x4	=8a	M z4	= 4qa2 .

Эпюра M z приведена на рис. 4.15, в.

После завершения III и IV операции при необходимости можно изобразить и реакции жесткой заделки.

В сечении заделки Е Qy = 4qa ; для того чтобы вертикальная

реакция в заделке вызвала такую перерезывающую силу, необходимо чтобы она была направлена вниз, т.е. стремилась повернуть примыкающую к заделке часть балки по часовой стрелке, как показано на рис. 4.15, г, и равна RE = 4qa .

Изгибающий момент в сечении Е M z = 4qa2 > 0 ; для того чтобы опорный момент M E вызвал положительный изгибающий мо-

мент (положительную кривизну оси балки), необходимо чтобы он был направлен против часовой стрелки, как показано на

рис. 4.15, г, и равен M E = 4qa2 .

П р и м е р 4 (рис.4.16)

I операция. Изображение расчетной схемы (рис.4.16, а).

II операция. Определение опорных реакций. Согласно фор-

муле (1.13) на с. 12 при числе замкнутых контуров K =1 , количестве простых шарниров Ш = 3 , S = 3 K − Ш = = 0 , т.е. задача статически определимая.

Представленная балка носит название балки с промежуточным шарниром.

Определение опорных реакций такой балки может быть произ-

ведено двумя методами.
Рассмотрим первый метод.
Неизвестных реакций опорных устройств – четыре: RB ,	RD ,
H D , M D . Уравнений равновесия можно записать только три:
∑X = 0 : H D = 0 ;	(1)

153

Рис. 4.16

154

∑mD = 0 :	M + RB 4a − 2qa 3a − P 2a + M D = 0 ;	(2)
∑mB = 0 ,	M + 2qa a + P 2a − RD 4a + M D = 0	(3)

Дополнительное четвертое уравнение можно записать из того соображения, что изгибающий момент в шарнире С равняется нулю. Изгибающий момент равен алгебраической сумме моментов, лежащих по одну сторону от сечения С. Тогда

∑M левая(C) = M + RB 2a − 2qa a = 0

(4)

(или ∑M правая(C) = RD 2a − M D = 0 ).

Решая совместно вышеприведенные четыре уравнения, получим

RB = 0,5P ; RD = 2,5P ; M D = 5Pa ; H D = 0 .

Рассмотрим второй метод.

Балка с промежуточным шарниром представляет собой сочлененную систему, состоящую из двух балок, соединенных шарниром С: правой консольной балки CD и левой полуподвесной балки

АС.

Мысленно разъединяем эти балки и изображаем их отдельно, заменяя их взаимодействие реакциями HC и RC (см. рис.4.16, б).

Силу Р, приложенную в сечении шарнира С, если специально не указано, можно отнести к правой балке CD (см. рис.4.16, б), или к левой балке АС, или разделить силу пополам и загрузить левую балку силой P / 2 в сечении С и правую балку силой P / 2 в сечении С.

Для полуподвесной балки АС запишем три уравнения равновесия:

∑X = 0 HC = 0 ;

∑mC = 0 : M + RB 2a − 2qa a = 0 RB = 0,5P ;

∑mB = 0 : M + 2qa a − RC 2a = 0 RC =1,5P .

Для консольной балки CD запишем три уравнения равновесия:

∑X = 0 : − HC + H D = 0 H D = 0 ;

∑mD = 0 : − P 2a − RC 2a + M D = 0 M D = 5Pa ;

∑mC = 0 : − RD 2a + M D = 0 RD = 2,5P .

155

Проверка правильности определения реакций производится так же, как и в примере 1.

Убедившись в правильности определения реакций, выносим их значения на расчетную схему (см. рис. 4.16, а).

III операция. Составление выражений для Qy и построение эпюры Qy . Силовых участков у балки три, при этом

				0 ≤ x1 ≤ a ,
				a ≤ x2 ≤ 3a ,
Qy	= 0 ;			0 ≤ x3 ≤ 2a .
1
Qy2	= RB − q(x2 − a)		(линейная зависимость!),
	при x2	= a	Qy2	= 0,5P ,
	при x2	= 3a	Qy2	= −1,5P .

Найдем абсциссу x20 ,	соответствующую значению Qy2 = 0 .
Для этого приравняем к нулю выражение для Qy2 :
Qy2 = RB − q(x20 − a) = 0 x20 =1,5a .
Qy = −RD = −2,5P = const	на всем участке DC.
3

Эпюра Qy представлена на рис.4.16, в.

IV операция. Составление выражений для M z и построение

эпюры M z .

M z1 = M = P a = const на всем участке АВ;

M z		= M + RB (x2		− a) − q	(x2 − a)		2	(квадратная парабола!),
	2					2
		при x2	= a	M z2		= M = Pa ,
		при x20 =1,5a		M z2		=1,125Pa ,
		при x2	= 3a	M z2		= 0 ,

последнее может служить проверочным моментом, так как действительно в сечении шарнира изгибающий момент равен нулю.

M z3 = RD x3 − M D (линейная зависимость!),

156

при x3 = 0 M z3 = −M D = −5Pa , при x3 = 2a M z3 = RD 2a − M D = 0 .

Эпюра M z приведена на рис. 4.16, г.

4.1.3. Проверка правильности построения эпюр Qy и M z

Анализ эпюр примеров 1 – 4, а также дифференциальные зависимости (4.3) и (4.4) позволяют установить правила, которые широко применяются для контроля правильности построения, и для совершенствования самой техники построения эпюр Qy и M z .

Приведенные далее правила, указания и выводы относятся к эпюрам балки, отнесенной к координатам с началом отсчета в левом крайнем сечении балки, т.е. ось х – горизонтальная ось, проведенная слева направо, а ось у – вертикально вверх.

4.3.1. Вертикальная сосредоточенная сила дает на эпюре Qy

скачок на величину силы (см. рис. 4.11, б, сечение А, D, К;

рис. 4.14, б, сечение А, С; рис.4.15, б, сечение С, Е; рис. 4.16, б, се-

чение В, С, D). На эпюре M z в сечении действия сосредоточенной

силы всегда получаем излом линии, ограничивающей эпюру, при этом острие излома направлено в сторону, противоположную направлению действующей силы. Это положение подтверждается

дифференциальной зависимостью Qy =

dM z

= tgβ. Так, на эпюре

dx

(см. рис. 4.11, б) в сечении D поперечная сила имеет два значения

Qy = −5qa (в сечении слева при x3 = 5a − 0 ) и Qy

= −qa (в сече-

3

3

нии справа при x3 = 5a + 0 ), следовательно, угол

наклона каса-

тельной

βправD

<

βлевD

(см. рис. 4.11, в); в сечении А, имеем одно

значение

Qy = 5qa , а левее сечения Qy

= 0 , т.е. βлев = 0 , и следо-

1

A

вательно, получаем две касательные, образующие угол, острие которого направлено в противоположную сторону направления реакции RA , т.е. вниз.

157

На эпюре (см. рис. 4.14, б) в сечении С имеем одно значение

	Qy (C) =	3M	> 0 , т.е.	βлев > 0 , а правее сечения С Qy = 0 , т.е.
		l
				C

βCправ = 0 , и следовательно, на эпюре M z (C) имеем две касатель-

ные, образующие угол, направленный острием против действующей силы RC , т.е. вверх (см. рис. 4.14, в).

На эпюре (см. рис. 4.15, б) в сечении С имеем два значения Qyлев2 (C) = −2qa < 0 и Qправy2 (C) = 4qa , т.е. на эпюре M z будем иметь в этом сечении две касательные к графику функции M z :

βCлев < 0 и βCправ > 0 , как показано на рис. 4.15, в; острие образо-

ванного угла направлено в сторону, противоположную направлению силы P = 6qa , т.е. вниз.

4.3.2. Сосредоточенный момент в сечении своего действия дает на эпюре M z скачек на величину момента (см. рис. 4.11, в, сечение Е; рис. 4.14, в, сечения А и В; рис. 4.15, в, сечения D и Е).

4.3.3. Если на участке q = 0 , то Qy = const (в том числе Qy = 0 ) и эпюра Qy ограничена прямой, параллельной оси х, а изгибаю-

щий момент изменяется по линейному закону, т.е. график функции

M z – прямая наклонная линия (см. на рис. 4.11 эпюры Qy и

M z на участках DE, ЕК; на рис. 4.14 эпюры Qy и M z на всем пролете балки; на рис. 4.15 эпюры Qy и M z на участках ВС, CD, DЕ; на рис. 4.16 эпюры Qy и M z на участке CD). Обращаем внимание, что при этом сосредоточенный момент, давая скачек на эпюре M z , не меняет угла наклона линии, ограничивающей эпюру M z , так

как Qy = dMdxz = tgβ = const на всем участке DK рис. 4.11, в, или, например, на всем пролете АС рис. 4.14, в. Таким образом, имеем, что на рис. 4.11, в прямая de ||e1k , на рис.4.14, в – ab ||b1c , на

рис.4.15, в – cd ||d1e .

158

4.3.4. Если на участке распределенная нагрузка имеет интенсив-

ность q = const , то Qy меняется	по	линейному	закону	(см.
рис. 4.11, б на участке ВС и CD;	рис. 4.15, б на		участке	АВ;
рис. 4.16, б на участке ВС), т.е. эпюра Qy		ограничена прямыми на-

клонными линиями, при этом если q < 0 , т.е. направлена вниз, то

Qy убывает, так как q = dQdxy = tgα < 0 , α < 0 . Если q > 0 , т.е. направлена вверх, то Qy возрастает.

Обращаем внимание, что в сечении перехода от одного значения q1 = const (или q = 0 ) к другому значению q2 = const , на эпюре

Qy получаем излом, что наглядно представлено на рис. 4.11, б. Здесь в сечении С пересекаются две прямые: одна под углом

dQy

α

BC

< 0

q

= q =

= tgα

BC

< 0

, и вторая под углом α

CD

< 0

1

dx

dQy

q

2

= 4q =

= tgα

CD

< 0

, при этом

α

CD

>

α

BC

. Излом на

dx

эпюре Qy имеется и в сечении В, где начинается распределенная

нагрузка интенсивностью q1 .

Особо подчеркнем, что «переходы» от одного значения интенсивности q к другому значению никак не сказываются на эпюре M z . Так на эпюре M z (см. рис. 4.11, в) в сечении В имеем плав-

ный переход наклонной прямой ab в кривую на участке ВС, что соответствует и дифференциальной зависимости Qy = dMdxz = tgβ,

так как в	этом сечении имеется только	одно значение
tgβ = Qy (B) =	= 5qa , т.е. в сечении к графику M z	можно провести

только одну касательную. Аналогичную ситуацию имеем и в сечении С.

4.3.5. Если на участке Qy = 0 , то M z = const (в том числе M z = 0 = const ), что имеет место на рис. 4.16, г на участке АВ.

159

4.3.6. Если на участке Qy > 0 , т.е. tgβ > 0 , то изгибающий момент

M z возрастает (см., например, рис. 4.11, в на участке АВ, ВС; рис. 4.14, в на участке АВ и ВС; рис. 4.15, в на участке CD и DE). И наоборот, если на участке Qy < 0 , т.е. tgβ < 0 , то M z убывает (см., на-

пример, рис. 4.11, внаучасткеDE, ЕК; рис. 4.15, внаучасткеАВиВС). 4.3.7. Если на участке эпюра Qy ограничена прямой наклонной

линией, т.е. Qy меняется по линейному закону, то эпюра M z ог-

раничена кривой второго порядка – параболой (см. рис. 4.11, в на участках ВС и CD; рис. 4.15, в на участке АВ; рис. 4.16, г на участке

ВС).

Знак кривизны параболы на эпюре M z можно определять по знаку второй производной от изгибающего момента. Так, если

	d 2 M z	= q > 0	, т.е.	1	> 0	, то эпюра M z	ограничена параболой во-
	dx2			ρ

гнутостью в положительное направление оси у (т.е. выпуклостью

	вниз). И, наоборот, если	d 2 M z	= q < 0 , т.е.	1	< 0	, то эпюра M z
		dx2		ρ

ограничена кривой выпуклостью вверх, как показано на рис. 4.11, в на участке BD, на рис. 4.15, в на участке АВ, на рис. 4.16, г на участке ВС.

4.3.7А. Однако более просто и удобно определять направление выпуклости (вогнутости) кривых на эпюре M z , причем для кривых

любой степени n или представляющих собой тригонометрическую функцию, исходя из следующих соображений, которые рассмотрим на конкретных примерах.

	qx	2
Для балки (см. рис. 4.15) на участке АВ M z = −	1		, т.е. эпю-
1	2

ра должна быть ограничена параболой. Обратимся к рассмотрению

	эпюры Qy		на этом участке. В сечении А Qy = 0 , следовательно,
	Qy =	dM z	= tgβ = 0 β = 0 , т.е. касательная к параболе в сечении
		dx

160