Исаченко Сопротивление материалов ч.1 2010

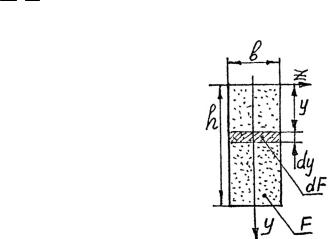
dW *

Из условия экстремума

z

= 0

получим

уравнение

dδ

1

= h ( δ

72δ2 − 40hδ+ 2h2 = 0 , корни которого будут

δ =

h

и δ

2

2

1

18

2

не имеет смысла). Подставляя

δ

в выражение для W * ,

получим

1

z

Wz* = h3 19 =1,05 Wz , т.е. прочность балки увеличится на 5 %. 24 18

Рис. 3.63

3.26. Площадь пор в элементарной площадке dF = b dy , отстоящей на расстоянии y от оси z (рис. 3.63),

dFпор = ρ( y) b dy = ρh0 by dy .

Так как поры в целом на 25 % ослабляют сечение, то, следова-

	h	ρ	b	y dy = 0,25 bh , откуда ρ0	= 0,5 .
тельно, Fпор = ∫dFпор = ∫		0
F	0	h

Найдем положение центра тяжести сечения по формулам (3.6), (3.7):

∫ y(dF −dFпор)

h

ρ

b

Sz

∫ y b −

0

y dy

4

y

=

=

F

=

0

h

=

h .

c

F

0,75bh

0,75bh

9

131

По формуле (3.3) момент инерции относительно оси z

	h			ρ				5
Iz = ∫ y2	(dF −dFпор) = ∫ y2	1	−		0	y	b dy =		bh3 .
								24
F	0			h

Тогда по формуле (3.12) найдем момент инерции относительно центральной оси, параллельной оси z,

		5		3	4		2		13		3
Izc	=		bh		−		h	0,75bh =		bh		.
		24				9			216

132

Тема 4

ПЛОСКИЙ ИЗГИБ ПРЯМОГО БРУСА

Плоским называется изгиб внешними нагрузками (сосредоточенные силы, распределенные нагрузки, пары сил), лежащими в одной плоскости, проходящей через главную центральную ось поперечного сечения, являющуюся осью симметрии, и осью бруса. Брус (стержень), испытывающий изгиб, принято называть балкой.

4.1. Построение эпюр внутренних силовых факторов

4.1.1. Предварительные замечания

Простейшими балками являются консольная (рис. 4.1) и простая однопролетная (рис. 4.2). Из этих двух балок можно составить самые разнообразные балки. Так, например, на рис. 4.3 изображена двухпролетная балка с правой консолью.

Рис. 4.1

Рис. 4.2

Рис. 4.3

Опоры у балок бывают трех видов.

133

1. Шарнирно-подвижная опора. Ее схематическое изображение, наиболее корректное для осуществления кинематического анализа, представлено на рис. 4.4, а. На рис. 4.4, б показаны и другие обозначения опоры, встречающиеся в литературе, которые нами использоваться не будут. В такой опоре возникает только одна опорная реакция, перпендикулярная опорной поверхности.

Рис. 4.4

Рис. 4.5

Рис. 4.6

2.Шарнирно-неподвижная опора (рис. 4.5, а). На рис. 4.5, б

представлено другое, встречающееся обозначение, которое в настоящем пособии использоваться не будет.

Втакой опоре возникают две опорные реакции R и Н, препятствующие вертикальному и горизонтальному смещению прилегающего к опоре сечения балки. Опора позволяет поворот прилегающего сечения балки. R и Н являются, по сути, вертикальной и горизонтальной компонентами реакции опоры, направленной под некоторым углом.

3.Жесткая заделка (защемление) (рис. 4.6). В такой опоре воз-

никают вертикальная R, горизонтальная Н опорные реакции и опорный момент М. Такая опора лишает прилегающее сечение балки всех трех степеней свободы в плоскости.

Принятое в настоящем пособии изображение опорных устройств позволяет устанавливать степень статической неопределенности балки по формуле (1.13): S = 3K − Ш . Так, для балки рис. 4.3 число

замкнутых контуров K = 3 (I, II, III), число шарниров Ш =8 , тогда

S=1 , т.е. балка один раз статически неопределимая.

Впоперечном сечении балки, испытывающей изгиб, возникают

вслучае поперечного изгиба два внутренних силовых фактора:

Qy – поперечная (или перерезывающая) сила и M z – изгибающий

134

момент. В случае чистого изгиба Qy = 0 , M z ≠ 0 . (Принятое рас-

положение осей представлено на рис. 4.3).

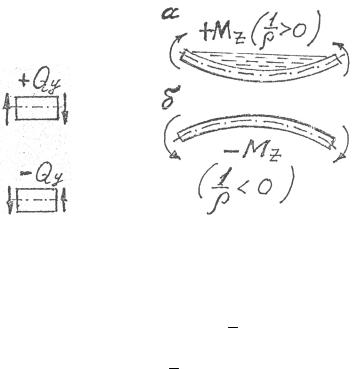
Правило знаков для Qy и M z . Поперечная сила Qy положи-

тельна, если она стремится повернуть часть балки, к которой приложена по часовой стрелке, и, наоборот, отрицательна – если стремится повернуть против часовой стрелки.

Рис. 4.7 иллюстрирует это правило.

Изгибающий момент положителен, если он стремится так изогнуть балку, чтобы верхние волокна испытывали сжатие, а нижние – растяжение (рис. 4.8, а), отрицательный изгибающий момент вызывает сжатие нижних волокон и растяжение верхних

(рис. 4.8, б).

Рис. 4.7

Рис. 4.8

Это же правило можно сформулировать исходя из знака кривизны в принятой системе координат:

изгибающий момент положителен, если его действие приводит к возникновению положительной кривизны ρ1 > 0 (см. рис. 4.8, а), и,

наоборот, M z отрицателен, если ρ1 < 0 (см. рис. 4.8, б).

135

Наиболее удобно определять знак изгибающего момента по мнемоническому «правилу воды»:

изгибающий момент положителен, если «налитая вода» (штриховая линия на рис. 4.8, а) удерживается (не стекает!) на поверхности балки, в противном случае (см. рис. 4.8, б) момент M z отрицателен.

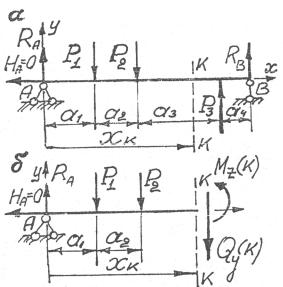
Определение величины Qy и M z в произвольном поперечном

сечении рассмотрим на примере сечения k − k для однопролетной балки (рис. 4.9, а).

Рис. 4.9

Воспользуемся методом сечений, для чего мысленно разрежем балку по сечению k − k и отбросим, например, правую часть балки. В сечении k − k (рис. 4.9, б) приложим положительные, соглас-

но принятому правилу знаков, Qy ,	M z и составим уравнения рав-
новесия:
∑y = 0 , RA − P1 − P2 −Qy (k) = 0	Qy (k) = RA − P1 − P2 , (4.1)

136

n
или Qy = ∑Pi ;	(4.1а)
1

∑mz = 0 , RA xk − P1(xk −a1) − P2 [xk −(a1 + a2 )]− M z (k) = 0 ,

где ось z, относительно которой берутся моменты, расположена в сечении k − k , а знак момента в уравнении равновесия ∑mz при-

нят положительным по часовой стрелке и отрицательным – против. Из последнего уравнения равновесия имеем:

M z (k) = RA x1 − P1(xk − a1) − P2 [xk −(a1 + a2 )],	(4.2)
n
или M z = ∑Mi .	(4.2а)
1

Анализ выражений (4.1) и (4.2) позволяет сократить графическую работу при решении задачи – отказаться от изображения отсеченных частей балки.

Из (4.1), (4.1а) следует, что:

перерезывающая сила в любом поперечном сечении равна алгебраической сумме сил, перпендикулярных к оси балки (параллельно оси y) и лежащих по одну сторону от сечения.

Внешняя сила, стремящаяся повернуть часть балки по часовой стрелке по отношению к рассматриваемому сечению, дает в выражении Qy положительное слагаемое, как, например, реакцию RA в

выражении (4.1); сила, стремящаяся повернуть часть балки против часовой стрелки, дает отрицательное слагаемое, как, например, сила P1 и P2 в выражении (4.1).

Из (4.2), (4.2а) следует, что:

изгибающий момент в любом поперечном сечении равен алгебраической сумме моментов внешних сил, лежащих по одну сторону от сечения, относительно рассматриваемого сечения (относительно оси z рассматриваемого сечения).

Внешние моменты, создающие положительную кривизну балки, дают в выражении M z положительные слагаемые, как, например,

момент RA x в выражении (4.2), и, наоборот – отрицательные слагаемые, если создают отрицательную кривизну, как, например, P1(xk − a1) и P2 [xk −(a1 + a2 )] в выражении (4.2).

137

Учитывая, что приведенные правила знаков для Qy и M z не свя-

заны с направлением выбранных осей координат, совершенно безразлично какая часть балки рассматривается лежащая слева или справа от сечения, т.е. можно брать абсциссу х как от левого конца балки вправо (как на рис. 4.9, а), так и от правого конца балки влево. Важно, чтобы выражения для Qy и M z были составлены наиболее

рационально, т.е. чтобы в них входило возможно меньшее число слагаемых. Так для сечений на участке a4 и a3 балки, изображенной на рис. 4.9, а, рационально абсциссы х взять от опоры В влево.

При построении эпюр Qy и M z пользуются дифференциаль-

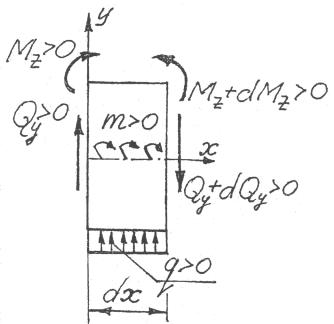
ными зависимостями между внешними усилиями и внутренними силовыми факторами. Дифференциальные зависимости, полученные из рассмотрения равновесия элемента балки длиной dx (рис. 4.10), на который действуют усилия с положительным знаком, имеют следующий вид:

q =	dQy	,	dM	z	= Qy + m ,	d 2M	z	= q +	dm	.	(4.3)
	dx		dx			dx2			dx

В большинстве задач интенсивность распределенной моментной нагрузки m = 0 , тогда дифференциальные зависимости принимают вид:

q =	dQy	= tgα , Qy =	dM	z	= tgβ, q =	d 2 M	z	.	(4.4)
	dx		dx			dx2

где α – угол между направлением оси абсцисс и касательной к графику функции Qy ; β – угол между направлением оси абсцисс и

касательной к графику функции M z .

Обращаем особое внимание, что в формулах (4.3) – (4.5) q > 0 направлено снизу вверх, т.е. совпадает с положительным направлением оси y на рис. 4.3, 4.10. Положительный угол α или β наклона касательной – это наименьший угол между направлением оси х и касательной, отложенный против часовой стрелки, и, наоборот, отрицательный – по часовой стрелке, при направлении оси х слева направо. Если ось х направлена справа налево, т.е. рассматривается правая часть балки от сечения, то в формулах (4.3) – (4.4) перед q и

138

Qy нужно проставить знак минус, так как угол наклона касательной меняет знак при изменении направления оси абсцисс.

	Рис. 4.10
Из выражения (4.4) имеем
Qy =	∫q dx ± Pi ,
	l	(4.5)
M z = ∫Qy dx ± Mi ,
	l

где постоянные Pi и Mi – это сосредоточенные силы и моменты,

лежащие по одну (рассматриваемую) сторону от данного сечения, при этом знак перед ними проставляется согласно правилу знаков для Qy и M z . Формулами удобно пользоваться в особенности при

построении эпюр от действия распределенной нагрузки q, изменяющейся по закону степенной или тригонометрической функции.

139

4.1.2. Порядок построения эпюр Qy , M z

Рассмотрим порядок построения эпюр на ряде примеров для балок, загруженных наиболее часто встречающимися внешними силами: сосредоточенными силами, сосредоточенными моментами, распределенными по длине нагрузками.

П р и м е р 1 (рис. 4.11)

I операция. Изображение расчетной схемы. Сюда входит изо-

бражение оси балки, опорных устройств, активных сил, реакций опор с указанием выбранного их направления, размеров силовых участков.

II операция. Определение опорных реакций. Приняв за нача-

ло координат точку А, изобразим координатные оси Y и Х. Составим уравнения равновесия в виде ∑X = 0 , ∑mK = 0 , ∑mA = 0 :

∑X = 0 H A = 0 ;

∑mK = 0 , RA 8a −2qa 6a −8qa 4a + P 3a − M = 0

RA = 5qa ;

∑mA = 0 , −RK 8a − M − P 5a +8qa 4a + 2qa 2a = 0 ,

откуда RK = qa .

Отметим, что при составлении уравнений действие равномерно распределенной по длине нагрузки заменяется действием ее равнодействующей, приложенной в центре тяжести нагрузки. Так, для нагрузки интенсивностью q2 равнодействующая равна q2 2a =

=8qa и приложена посредине отрезка CD.

При составлении уравнения вида ∑mi = 0 для моментов при-

нимается правило знаков: по часовой стрелке – знак «+», против часовой стрелки – «–», или наоборот. И совершенно неуместно вспоминать о правиле знаков для изгибающих моментов, так как в этом случае имеем дело исключительно с уравнениями статики.

Для проверки правильности определения опорных реакций воспользуемся уравнениями, являющимися следствием вышеприведенных уравнений равновесия. Как известно из курса теоретической механики уравнение вида ∑Y = 0 является следствием урав-

нений ∑mA = 0 и ∑mK = 0 , как сумма проекций на ось, перпендикулярную прямой, соединяющей точки А и К. Уравнение вида

140