Исаченко Сопротивление материалов ч.1 2010

M z (1 −1)

=

qa2

,

(*)

2

M z (2 − 2) = RB x(2−2) −

q[x(2−2)

]2

.

(**)

2

l

Из уравнения равновесия в виде ∑mA = RB (l − a) − ql

− a

=

2

= 0 найдем RB = ql

l − 2a

.

2(l − a)

На участке АВ нас будет интересовать абсцисса того сечения, в

	котором действует M z(max) (2 − 2) .
	Из Qy (2 − 2) = RB − qx(2−2) = 0 найдем	x0 = l	l − 2a	. Тогда
			2(l − a)
	подставляя вместо x(2−2) значение x0 в	(**)	и приравнивая
	M z (2 − 2) = M z (1 −1) , найдем a = 0,293l .

211

Тема 5

ПЕРЕМЕЩЕНИЯ В БАЛКАХ ПРИ ПЛОСКОМ ИЗГИБЕ

5.1. Предварительные замечания

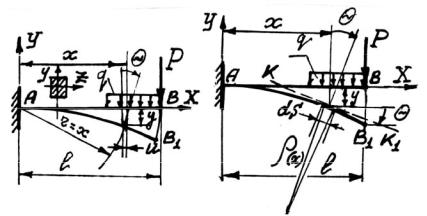
Под действием внешних сил ось балки искривляется (рис. 5.1) и сечения балки получают линейные и угловые перемещения u, y, θ. Перемещение u настолько мало, что им можно пренебречь, тогда изогнутая ось балки или, иначе, упругая линия балки будет иметь вид AB1 , показанный на рис. 5.2, где y – прогиб сечения х, т.е. пе-

ремещение центра тяжести сечения по направлению, перпендикулярному оси балки в плоскости изгиба.

Рис. 5.1 Рис. 5.2

Наибольший прогиб (прогиб сечения В на рис. 5.2) называется стрелой прогиба и обозначается через f.

Уравнение вида y = F(x) будет являться уравнением изогнутой оси балки.

212

Угол поворота θ поперечного сечения равен углу наклона касательной KK1 к изогнутой оси с первоначальной (до деформирова-

ния) осью x; как известно: tgθ = dydx .

Угол θ на практике при изгибе балок очень мал, обычно он не более одного градуса, и с достаточной степенью точности можно

	считать, что tg θ ≈ θ в радианах, тогда
	θ =	dy	,	(5.1)
		dx

т.е. угол поворота поперечного сечения равен первой производной по х от прогиба y в данном сечении.

5.2. Дифференциальное уравнение изогнутой оси балки

Кривизна изогнутой оси связана с изгибающим моментом выражением:

1

=

M z (x)

,

(5.2)

ρ(x)

EJ z (x)

где ρ(x) – радиус кривизны изогнутой оси между двумя смежными

сечениями, т.е. радиус кривизны дуги длиной dS (см. рис. 5.2).

Из курса высшей математики известно, что

±

d 2 y

1

=

dx

2

.

(5.3)

ρ(x)

dy

2

3

+

1

dx

Приравнивая правые части выражений (5.2) и (5.3) и сохраняя

только знак «+» в последнем выражении, так как имеется полное соответствие между знаками кривизны и знаком изгибающего момента, что продемонстрировано на рис. 5.3, получим точное уравнение изогнутой оси балки:

		d 2 y
		dx2					=	M z (x)	.	(5.4)
								EJ z (x)
		dy			2	3
	+
1
		dx

213

Рис. 5.3

Интегрирование нелинейного дифференциального уравнения второго порядка (5.4) представляет значительные трудности, c другой стороны, квадрат угла поворота θ = dy / dx – величина весьма

малая по сравнению с единицей. Учитывая это, для определения перемещений используют приближенное дифференциальное уравнение, которое принято называть основным дифференциальным уравнением упругой линии:

	EJ z (x)	d 2 y		= M z (x) .	(5.5)
		dx	2

В большинстве задач EJ z (x) = EJ z = const , тогда двумя последовательными интегрированиями получим выражения для определения θ и y:

	EJ z	dy	= EJ z θ = ∫M z (x) dx + C ,	(5.6)
		dx
	EJ z y = ∫dx∫M z (x) dx + C x + D .			(5.7)

Если жесткость EJ z (x) – величина переменная, то понятно, что

она должна быть внесена под знак интеграла.

Постоянные интегрирования С и D определяются из граничных условий (условий на опорах и на границе двух смежных участков).

При расположении осей х и y, как показано на рис. 5.1 – 5.3, руководствуемся следующим правилом знаков: положительный прогиб y направлен в положительное направление оси y, а отрицательный – в отрицательное; угол θ положителен, если сечение поворачивается против часовой стрелки, и отрицателен – если по часовой стрелке от своего первоначального положения.

214

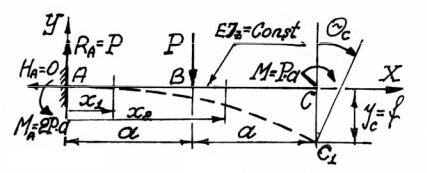
П р и м е р 1

Определить прогиб и угол поворота сечения С консольной бал-

ки (рис. 5.4).

Рис. 5.4

I операция. Изображение расчетной схемы. Сюда входит изо-

бражение балки (ее оси!), ее размеров, опорных устройств, активных сил, реакций опор с указанием выбранного их направления, изображение выбранной координатной системы.

II операция. Определение опорных реакций. Составляем уравнения равновесия:

∑X = 0 H A = 0 ,

∑Y = 0 RA = P ,

∑mA = 0 , − M A + Pa + M = 0 M A = 2Pa .

Для проверки правильности определения опорных реакций можно воспользоваться, например, уравнением вида ∑mC = 0 .

III операция. Составление уравнений упругой линии для каждого силового участка и интегрирование их:

			EJ z y1′′ = −2Pa + Px1 ,
									Px	2
EJ z y1′			= EJ z θ1 = −2Pax1					+	1		+ C1 ,		(1)
						Px13			2
EJ	z	y	= −	2Pax12	+			+ C x			+ D	,	(2)
		1	2		6				1	1	1

EJ z y2′′ = −2Pa + Px2 − P(x2 − a) ,

215

EJ z y2′ = −2Pax2 +

Px22

−

P(x2 − a)2

+ C2 ,

(3)

2

2

EJ z y2

2Pax22

Px23

P(x2

− a)3

+ C2 x2 + D2 .

= −

+

−

(4)

2

6

6

IV операция. Определение постоянных интегрирования Ci и

Di . Из условия опирания (заделки) левого сечения А:

при x1 = 0	y1′ = θA = 0	C1 = 0 ,
	y1 = y A = 0 D1 = 0 .

Из условия на границе смежных участков АВ и ВС:

при x1 = x2 = a y1′ = y2′ C1 = C2 = 0 , y1 = y2 D1 = D2 = 0 .

V операция. Определение перемещений в заданных сечени-

ях. Подставляя в (3) x2 = 2a найдем y2′					(C) = θC = −	2,5Pa2
							(ради-
						EJ z
ан), а из (4) найдем	y2 (C) =	f = −	17Pa3		(м).
			6EJ z

На рис. 5.4 изогнутая ось показана штриховой линией.

Из уравнений (1) и (2) следует, что постоянные интегрирования

С = EJ

z

θ

A

= EJ

z

θ

0

[Н м2 ] , а D = EJ

z

y

A

= EJ

z

y

0

[Н м3

] ,

1

1

где y0

– прогиб,

θ0

– угол поворота в начале координат. Постоян-

ные C1 и D1 обратились в нуль, что является следствием выбора начала координат в заделке.

5.3.Метод начальных параметров (метод Клебша). Универсальное уравнение упругой линии

При определении перемещений путем интегрирования дифференциальных уравнений упругой линии, получаем 2n постоянных интегрирования, где n – число силовых участков. Можно обеспечить равенство между собой всех соответствующих постоянных интегрирования, если при интегрировании соблюдать следующие правила.

1. Начало координат выбирается в крайнем левом сечении балки.

216

2. Абсцисса xi текущего сечения для каждого силового участка

отсчитывается от один раз выбранного начала координат.

3. Если имеется сосредоточенный момент, то в уравнении изгибающего момента он должен быть умножен на скобку (x − a)0 , равную единице. Здесь а – абсцисса сечения приложения момента М.

4.Интегрирование должно проводиться без раскрытия скобок.

5.Распределенная нагрузка раз начавшись должна продолжаться до конца балки. Если распределенная нагрузка обрывается, то ее продлевают «дополнительной» нагрузкой до конца балки, а для восстановления исходного нагружения балку догружают «компенсирующей» нагрузкой обратного направления.

При выполнении приведенных правил С1 = С2 =... = Ci = C0 =

= EJ z θ0 , D1 = D2 =... = Di = D0 = EJ z y0 ; в уравнивании постоянных интегрирования и состоит сущность метода начальных па-

раметров. Прогиб y0 и угол поворота θ0 в начале координат при-

нято называть начальными параметрами.

При решении задач методом Клебша легко заметить, что сосредоточенные моменты дают в уравнении прогибов члены вида

		M (x − a)2	(где а – абсцисса сечения, в котором приложен сосре-
	2
				P(x − a)3
	доточенный момент М), сосредоточенные силы –				(где
				6

а – абсцисса сечения, в котором приложена сосредоточенная сила

	P), равномерно распределенные нагрузки –	q(x − a)4	(где а – абс-
		24

цисса начала приложения распределенной нагрузки), распределен-

	ная по треугольнику нагрузка –	tg β(x − a)5	, где β – положитель-
		120

ный угол наклона касательной к эпюре треугольной нагрузки.

С учетом указанного было составлено универсальное уравнение метода начальных параметров упругой линии балки:

		x1		M	i	(x − a)2		P	(x − a)3
EJ z y = EJ z y0	+ EJ z θ0		± ∑				± ∑	i		±
		1!				2!			3!

217

± ∑	qi (x − a)4	± ∑	tg β(x − a)5	.	(5.8)
4!		5!
В уравнении (5.8) EJ z y0 = D0 , а EJ z θ0 = C0					(см. уравнения

(2) и (4) в III операции примера 1). Знак «+» или «–» перед членами уравнения определяется знаком изгибающих моментов, которые вызывают соответствующие нагрузки в сечении с абсциссой х. При составлении универсального уравнения абсцисса х – это абсцисса текущего сечения последнего (правого) силового участка балки.

Определение начальных параметров y0 и θ0 производится из

граничных условий – условий на опорах балки.

Дифференцируя уравнение (5.8) получим уравнение для определения углов поворота поперечных сечений балки:

EJ z θ = EJ z θ0	± ∑	M i (x − a)1		± ∑	Pi (x − a)2		± ∑	q(x − a)3	±
	1!			2!			3!
		± ∑	tg β(x − a)4			.	(5.9)
				4!

Правило знаков для θ и y сохраняется то же, что и в методе интегрирования дифференциальных уравнений изогнутой оси балки.

При определении перемещений с помощью (5.8), (5.9) в уравнениях используются только те члены, у которых x > a , другими словами, учитываются только те усилия, которые лежат по одну сторону (левее!) рассматриваемого сечения с абсциссой х, т.е. те члены, у которых (x − a) > 0 .

При составлении уравнения (5.8) балка просматривается от начала координат. При этом с появлением той или иной нагрузки записывают член уравнения, соответствующий данной нагрузке.

П р и м е р 2

Для балки (рис. 5.5, а) определить прогиб сечения С и угол поворота сечения D. Изобразить изогнутую ось балки. Балка изготов-

лена из двутавра 27а, для которого J z = 5500 см4 ; l = 2 м, q = 20 кН/м, E = 2 105 МПа.

218

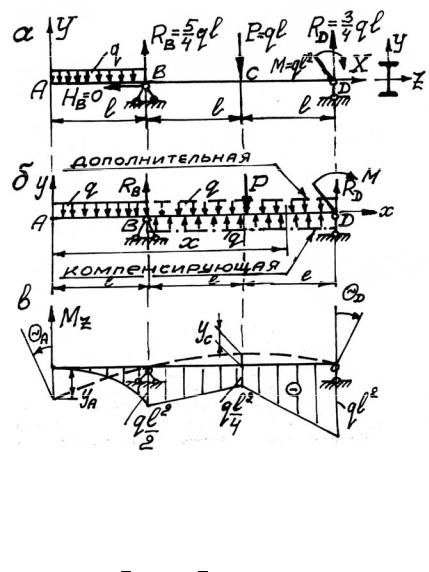
Рис. 5.5

I операция. Изображение расчетной схемы (см. рис. 5.5, а) II операция. Определение опорных реакций. Используя урав-

нения равновесия вида ∑X = 0 , ∑mD = 0 , ∑mB = 0 , найдем,

что H B = 0 , RB = 54 qa , RD = 34 qa . Проверку правильности опре-

деления реакций осуществим, составив уравнение вида ∑Y = 0 .

219

III операция. Составление расчетной схемы с учетом правил метода начальных параметров (рис. 5.5, б), а именно правил 1 – 5

разд. 5.3 на с. 216, 217.

IV операция. Составление универсального уравнения:

EJ z y = EJ z y0 + EJ z θ0 x −			q(x −			0)	4	+	RB (x − l)3	+
					4!				3!
									x>l
+	q(x − l)4	−			P(x − 2l)3				.	(5.10)
	4!					3!

x>2l

Значения x > l и x > 2l под стрелками указывают, что все члены уравнения, находящиеся правее вертикальной разделительной черты, используются в решении, если х имеет указанное значение.

V операция. Определение начальных параметров. При y = yB = 0 :

0 = EJ z y0 + EJ z θ0l −

ql 4

.

24

При x = 3l y = yD = 0 :

5

q(3l)

4

ql

(3l

− l)3

0 = EJ z y0 + EJ z θ0 3l −

4

+

+

6

q(3l − l)4

24

2l)3

+

−

ql(3l −

.

24

6

Решая совместно уравнения (1) и (2), найдем

y0 = y A = −

13

ql 4

= −1,58 10−2 м,

24 EJ z

θ0

= θA =

14 ql3

= 0,0084 рад = 0,482°.

24 EJ z

x = l

(1)

(2)

220