Исаченко Сопротивление материалов ч.1 2010

с известным значением интенсивности q. Если балку догрузить силой P, то при каком значении этой силы прогиб балки в сечении А будет равен нулю?

Задача 5.3. Для балки с промежуточным шарниром (рис. 5.20), которая имеет постоянную жесткость EJ z = 7300 кН м2 , постро-

ить изогнутую ось, определив перемещения необходимых сечений.

Дано: Р = 40 кН, M = 40 кН м , а = 1 м.

Рис. 5.20

Рис. 5.21

Задача 5.4. Для однопролетной балки с правой консолью (рис. 5.21), нагруженной на конце консоли силой Р, замерен максимальный прогиб ymax = f на пролете между опорами. Опреде-

лить наибольшее значение нормальных напряжений в опасном поперечном сечении балки и величину силы Р. Известны размеры прямоугольного поперечного сечения, длина l пролета и модуль упругости Е для материала балки.

Задача 5.5. Однопролетная балка загружена распределенной нагрузкой, как показано на рис. 5.22. Определить прогиб посредине пролета балки, если жесткость поперечного сечения EJ z постоян-

на по всей длине.

241

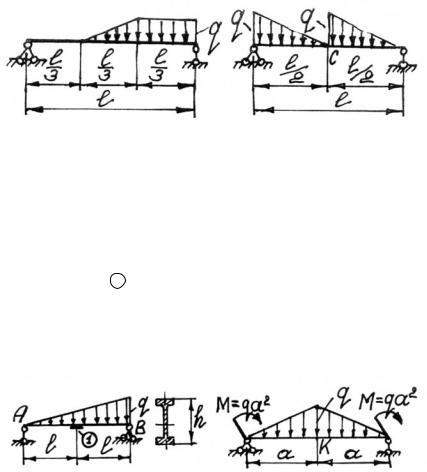
Рис. 5.22

Рис. 5.23

Задача 5.6. Однопролетная балка загружена распределенными по линейному закону нагрузками с наибольшей интенсивностью q (рис. 5.23). Определить прогиб сечения С балки, если жесткость ее

EJ z = const.

Задача 5.7. Однопролетная балка (рис. 5.24) загружена распределенной нагрузкой, изменяющейся по линейному закону. Изме-

ренная датчиком 1 продольная деформация составила ε = 5 10−4 . Найти взаимный угол поворота сечений А и В, если l = 15h.

Задача 5.8. Балка (рис. 5.25) загружена распределенной нагрузкой и сосредоточенными моментами. Определить угол поворота поперечного сечения K, если жесткость EJ z = const.

Рис. 5.24

Рис. 5.25

Задача 5.9. Для балки (рис. 5.26), загруженной сосредоточенными моментами M = q0l 2 и распределенной нагрузкой, изменяющейся по

закону q = q0 sin πlx , найтипрогибсеченияK, если EJ z = const.

Задача 5.10. Балка постоянной жесткости EJ z с промежуточным шарниром K (рис. 5.27) нагружена парой сил моментом M в

242

двух вариантах: слева и справа от шарнира K. Найти линейное перемещение шарниров, угол поворота сечений приложения момента M и работу пары сил в обоих вариантах. Дано: M, l, E, J z .

Рис. 5.26

Рис. 5.27

Задача 5.11. Однопролетная балка (рис. 5.28) постоянной жесткости поперечного сечения EJ z загружена по двум вариантам:

железобетонной плитой (см. рис. 5.28, а), деформацией которой пренебрегаем, весом G;

мешками с песком (см. рис. 5.28, б), равномерно распределенными надлине2l балки, имеющими общийвес G, равныйвесуплиты.

Рис. 5.28

Определить, насколько отличается максимальный прогиб в балке в обоих вариантах нагружения.

Рис. 5.29

243

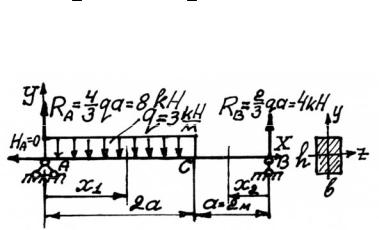
Задача 5.12. Для балки постоянной жесткости поперечного сечения EJ z (рис. 5.29) найти расположение опор, при котором от указанной нагрузки прогиб посредине балки будет равен нулю.

5.7.Решения, указания, ответы

5.1.Изобразим расчетную схему (рис. 5.30). Используя уравнения равновесия в виде ∑X = 0 , ∑mB = 0 , ∑mA = 0 , найдем, что

H A = 0 , RA = 43 qa =8 кН, RB = 23 qa = 4 кН. Проверку правильно-

сти определения реакций опор выполним, составив уравнение вида

∑Y = 0 .

Рис. 5.30

Для того, чтобы получить более простые выражения изгибающих моментов для силового участка АС абсциссу текущего сечения x1 будем отсчитывать от опоры А, а для силового участка ВС – x2

будем отсчитывать от опоры В.

Составим дифференциальные уравнения изогнутой оси балки для каждого силового участка и дважды проинтегрируем их:

qx2

EJ z y1′′ = RA x1

−

1

,

EJ z y2′′ = RB x2 ;

2

EJ z y1′ =

RA x12

−

qx13

+ C1 , (1)

EJ z y2′ =

RB x22

+ C2 ; (2)

2

2

6

244

			RA x3		qx4								R	B	x	2
EJ	z	y =	1	−	1	+ C x	+ D , (3)	EJ	z	y	2	=					+ C	2	x	2	+ D	2	. (4)
		1	6		24	1 1	1							6

Для определения постоянных интегрирования воспользуемся граничными условиями:

при x1	= 0 :	y1 = 0 D1 = 0 ;
при x2 = 0 :		y2 = 0	D2 = 0 ;
при x1	= 2a и x2 = a :		y1 = y2 = yC ,	(а)
			θ1 (С) = −θ2 (С) ,	(б)

здесь знак «–» (минус) перед θ2 (С) объясняется тем, что оси x1 и x2 направлены в противоположные стороны, поэтому правило знаков для θ2 меняется на обратное, по отношению к правилу зна-

ков для θ1 .

Условие а) приводит к следующему выражению:

RA (2a)3	−	q(2a)4	+ C 2a =	RB a3	+ C	2	a .
6	24		1	6

Условие б) дает равенство:

RA (2a)2 − q(2a)3 + C = −				RB a2	− C		.
2		6	1	2		2

Подставляя численные значения в последние два равенства, получим

72 + 6C1 = 3C2 ,

40 + C1 = −C2 ,

откуда C1 = −21,3 кН м2 , С2 = −18,7 кН м2 .

Для определения абсциссы сечения, которое имеет наибольший прогиб, исследуем на экстремум уравнение (3):

dy	= 0 :	RA x12	−	qx13	+ C = 0	xmax = 2,889 м.
dx		2	6		1	1

Поставив x1max в выражение (3), получим ymax = f = 3,818 10−2 м.

245

Обращаем внимание, что постоянная C1 ≠ C2 , это определено

тем, что не был применен метод уравнивания постоянных интегрирования (метод Клебша).

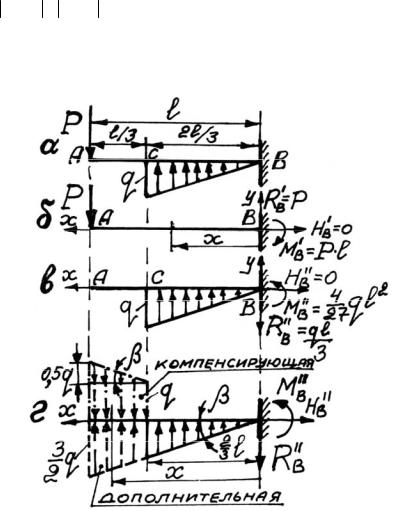
5.2. Прогиб сечения А (рис. 5.31, а) будет равен нулю, если y A (P) = y A (q) .

Для определения прогиба y A (P) воспользуемся расчетной схе-

мой, изображенной на рис. 5.31, б. Начало координат расположим в сечении В.

Рис. 5.31

246

Универсальное уравнение будет иметь вид:

		′			3		′	2
EJ z y(P) = EJ z y0 + EJ z θ0 x +	RB (x − 0)					−	M B (x − 0)		.
			3!				2!
В заделке yB = y0 = 0 , θB = θ0 = 0 , тогда при x = l
y A (P) = −		Pl3		,
		3EJ z

где знак «–» (минус) свидетельствует о том, что прогиб y A (P) направлен в сторону, противоположную оси y, т.е. вниз.

Для определения прогиба y A (q) воспользуемся расчетной схемой (рис. 5.31, в), для которой из уравнения равновесия в виде ∑x = 0 ,

∑y = 0 , ∑mB = 0 найдем, что	′′	,	′′	ql	,	′′	4ql 2	.
	H B = 0		RB =	3		M B =	27

Проверку правильности определения реакций опоры В можно выполнить, составив уравнение равновесия вида ∑mC = 0 , которое являет-

сяследствиемуравнений ∑y = 0 и ∑mB = 0 .

Внесем коррективы в нагрузку на балку (рис. 5.31, г) согласно требованиям метода начальных параметров. Тогда универсальное

уравнение (с учетом того, что

yB = y0 = 0

и

θB = θ0 = 0 ) будет

иметь вид:

′′

0)

2

′′

3

tg β(x − 0)

5

EJ z y(q) =

M B (x −

−

RB (x − 0)

+

−

2!

3!

5!

2

4

2

5

q x −

l

tg β x

−

l

3

3

−

−

,

4!

5!

x>

2

l

3

где tg β =		q		.
		2	l
		3

247

Тогда при x = l

y A (q) =

37ql 4

.

15

81

EJ z

37

Из равенства

y A (P)

= y A (q)

получим, что P =

ql =

5 81

=0,091ql .

5.3.Заданную балку представим как состоящую из двух: однопролетной с правой консолью и полуподвесной (рис. 5.32, а).

Используя уравнения равновесия, найдем реакции опор и силы взаимодействия в шарнире D (полученные численные значения реакций приведены на рис. 5.32, а).

На рис. 5.32, б изображена эпюра изгибающего момента для всей заданной балки.

Для построения изогнутой оси балки найдем прогибы сечений В, S, D и углы поворота сечений S, D для левой балки, а также угол поворота сечения D для правой балки с помощью универсального уравнения.

Для левой (AD) балки при начале координат в сечении А:

л			л	RA (xл − 0)		3		M (xл − a) 2
EJ z yл = EJ z y0	+ EJ z θ		0 xл −	3!			+	2!	+
								xл>a
	+	RC (xл − 4a)3			.				(1)
			3!

xл>4a

Найдем начальные параметры из граничных условий: при xл = 0 : yл = y0л = 0 ,

при xл = 4a = 4 м:	yл = yC = 0 θ0л = θA =	100	=
		12EJ z

= 0,00114 рад = 0,0655°.

Подставляяв(1) значения xл =1м, xл = 2 ми xл = 6 м, найдем, что: yB = 0,0007 м = 0,7 мм;

yS = 0,00137 м = 1,37 мм; yD = −0,016 м = –16 мм.

248

Рис. 5.32

Для определения углов поворота сечений продифференцируем уравнение (1):

249

dyл

л

RA (xл − 0)

2

M (xл − a)1

EJ z

= EJ zθл = EJ z θ0

−

+

+

dx

2!

1!

xл>a

+

RC (xл − 4a)2

.

(2)

2!

xл>4a

При xл = 2

м: θS = 0,00113 рад = 0,065°.

При xл = 6

м: θлD = −0,0098 рад = –0,563°.

Составим универсальное уравнение для правой (DN) балки, выбрав начало координат в сечении D:

п		п	RD (x − 0)3			P(x − 2a)3
EJ z yп = EJ z y0	+ EJ z θ	0 xп +			−			,	(3)
			3!			3!
где y0п = yD = −16 мм.						x>2a
Из условия, что при xп = 4a : yп = yN = 0 найдем
θ0п = θпD = −0,0015 рад = –0,085°.
Изогнутая ось	балки	изображена		(сплошная			линия)		на

рис. 5.32, в, где масштаб прогибов и углов поворота существенно увеличен по сравнению с масштабом размеров балки.

5.4. Используя уравнения равновесия, найдем реакции опор балки (рис. 5.33, а). Построим эпюру изгибающего момента M z (рис. 5.33, б), откуда следует, что опасным сечением является сечение В, где действует M z(max) = Pl / 2 .

Запишем универсальное уравнение для балки с учетом, что y0 = y A = 0 при расположении начала координат на опоре А.

		RA (x − 0)3		RB (x − l)3
	EJ z y = EJ z θ0 x +		−		.	(1)
		3!		3!

x>l

250