Исаченко Сопротивление материалов ч.1 2010

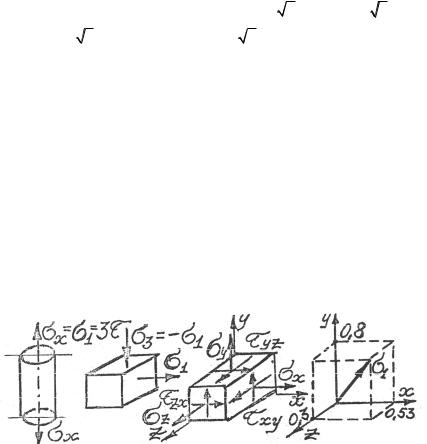
	2.3. Решения, указания, ответы
2.1. Для напряженного состояния (рис. 2.7, а)		II ≠ 0 ,	III =
= IIII	= 0 , т.е. имеем линейное напряженное состояние. По формуле
(2.1)	найдем σi = 3τ = σ1 = σx ; σj = σk = 0 (рис. 2.23). Для напря-
женного состояния (см. рис. 2.7, б) имеем II = 0 , III		≠ 0 , IIII	= 0 ,

т.е. элемент испытывает двухосное напряженное состояние. По

формуле (2.1)	получим σi = 0 , σj = τ 2 , σk = −τ 2 , т.е.
σ1 = σj = τ 2 ,	σ2 = σi = 0 , σ3 = −τ 2 – напряженное состояние,

эквивалентное чистому сдвигу (рис. 2.24).

2.2. 1. Отнесем элемент к осям x, y, z (рис. 2.25), тогда σx =

=40 МПа, σy = 90 МПа, σz = 30 МПа, τxy = 60 МПа, τyz = 30 МПа,

τzx = 20 МПа.

2. Определим инварианты II = 40 +90 +30 =160		МПа,
III = 2600 МПа2, IIII = 0 , т.е.	имеем двухосное напряженное со-
стояние. Из уравнения (2.1)	получим σi = 0 , σj =141,6	МПа,

σk =18,4 МПа. Итак, имеем: σ1 = σj , σ2 = σk , σ3 = 0 .

3. Для определения направления σ1 подставим в формулу (2.5) вместо σ = σ1 = σj и найдем направляющие косинусы l = 0,53; m = 0,8; n = 0,3 (рис. 2.26).

Рис. 2.23

Рис. 2.24

Рис. 2.25

Рис. 2.26

81

2.3. Вариант 1. Для того чтобы элемент испытывал одноосное напряженное состояние, необходимо второе главное напряжение по формуле (2.9) приравнять к нулю, т.е.

σj =	σx +σy	−		σx −σy	2 + τ2xy = 0 σx σy = τ2xy .
	2
			2

Вариант 2. Нулю должен быть равен второй инвариант

III =		σx		τyx			= 0 , откуда σx σy = τ2xy .
		τ	xy	σ	y

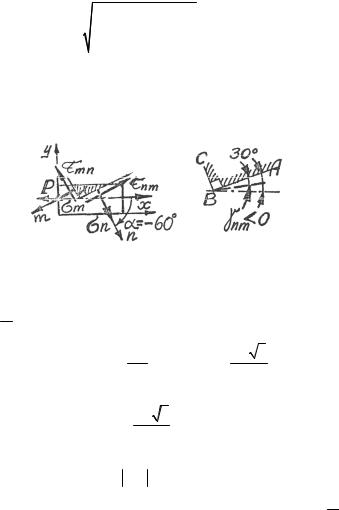
Рис. 2.27 Рис. 2.28

2.4. Отнесем стержень к координатным осям x, y (рис. 2.27). Тогда σx = FP , σy = 0 , τxy = 0 , и по формуле (2.7)

τnm = σ2x sin 2α = 2PF (−cos30)= − P4F 3 < 0 ,

т.е. τnm на площадке n направлено против часовой стрелки. По формуле (2.12) γnm = τGnm = − P4GF3 < 0 , т.е. площадка АВ поворачивается на угол γnm по часовой стрелке и, следовательно, прямой угол АВС увеличивается на γnm (рис. 2.28).

2.6. В поперечном сечении действует только σx = σ1 = FP . На

	площадке I и II, для которых	α = (x, n)= −45D , напряжения опре-
	делим по формулам (2.6)	и (2.7): σn =	σx	+	σx cos 2α =	σx ,
			2
					2	2

82

τnt = σ2x sin 2α = −σ2x . На площадке III σn = 0 и τnt = 0 , так как она

|| σx .

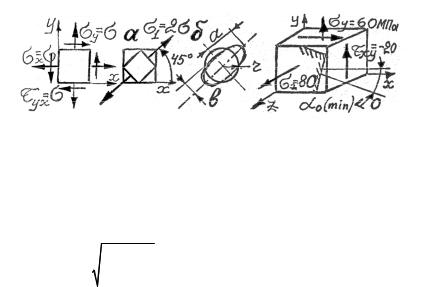
2.6. Отнесем элемент к осям x, y (рис. 2.29). Главные напряже-

ния определятся по формуле (2.9): σi = 2σ,

σj = 0

, т.е. имеем од-

ноосное напряженное состояние при σ1 = σi

= 2σ. Направление σ1

определим

по

формуле

(2.10):

tg 2α0 =

−2 (−σ)

= ∞

σ−σ

2α0 = 90D,

α0 = 45D (рис. 2.30, а). Круг превращается в эллипс

(рис. 2.30, б),

для

которого

ε = σ1

= 2σ

,

ε

2

= ε

3

= −με = −μ 2σ .

1

E

E

1

E

Размеры полуосей эллипса: a = r + r ε1 , b = r + r ε2 .

Рис. 2.29 Рис. 2.30 Рис. 2.31

2.7. Отнесем элемент к координатным осям x, y, z (рис. 2.31), тогда σx = 0 , σy = 60 МПа, σz =80 МПа, τxy = −20 МПа. Одно главное напряжение известно: σz = σk =80 МПа. Для определения двух других главных напряжений воспользуемся формулой (2.9):

σi (σj )=

σy

±

σ2y

+ τ2xy = 30 ±36 .

Таким

образом,

имеем:

4

2

σ1 = σz

=80 МПа, σ2 = σi

= 66 МПа,

σ3 = σj = −6

МПа. Из фор-

мулы

(2.10)

получим

положение

главной площадки:

tg2α0 =

−2 τxy

α0(min)= (x, σj )= −16

D

50

′

.

τmax =

σ1

−σ3

=

0 −σy

2

83

= 43,0 МПа и действует на площадке || σ2 = σi и расположенной под углом 45° к направлению σ1 = σz и σ3 = σj .

2.8. В любом поперечном сечении бруса по формулам сопротивления материалов действует нормальное напряжение

P

σx = F (x) < 0 . Выделим у боковой грани бруса элемент АВС раз-

мерами dx ×dy ×1 (толщина бруса принята за единицу), как показано на рис. 2.32. На грани ВС, как в поперечном сечении, действует напряжение σx (рис. 2.33, а). Сила dNx = σx 1 dy может быть уравновешена только силой dT = τxy 1 dx от действия τyx на грани АВ (рис. 2.33, б). Тогда, согласно закону парности касательных напряжений, на грани ВС будет действовать τxy = τyx

(рис. 2.33, в). Сила dT1 = τxy 1 dy может быть уравновешена только силой dN y = σy 1 dx от действия σy на грани АВ (рис. 2.33, г).

Рис. 2.32

Рис. 2.33

2.9. На участке длиной a в каждой точке имеем двухосное напряженное состояние: σx = 0 ; σy = −p , σz = −p . Тогда

εx =	1	σx −μ(σy + σz )		=	2 p μ	=	a	l =	a =	2 pμa .
					E		a
	E									E

2.10.В ленте имеет место линейное напряженное состояние:

σx = σ1 = NFx = FP , где F = bδ. Так как μ = 0,5 , то согласно форму-

ле (2.12) εv = 1 −E2μ σx = 0 , т.е. объем ленты до и после наматыва-

ния на валик будет один и тот же (рис. 2.34):

84

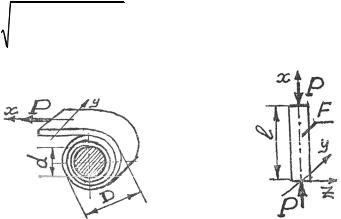
V = bl δ =	π(D2	− d 2 )	b	,
4			1

где b1 – ширина ленты после деформирования. Новую ширину b1

найдем из следующего:

b = b + b , ε

y

=

b

,

откуда

b = bε

y

, а

1

b

σx

P

b = −μP

так как

εy = −μεx = −μ

= −μ

,

то

. Тогда

E

EF

δE

b =

bδE −μP

. Подставляя

значение

b

в V,

получим

1

δE

1

D = d 2 +

4lbδ2 E

.

π(bδE −μP)

Рис. 2.34 Рис. 2.35

2.11. Для стержня (рис. 2.35) напряжения в поперечном сечении

σ

x

= −

P

;

относительное

изменение объема

ε = V

=

F

V

V

P

=

1 − 2μ σx = −

(1 − 2μ), откуда

EF

E

Pl (1 − 2μ)

V =V ε = Flε = −

.

V

V

E

85

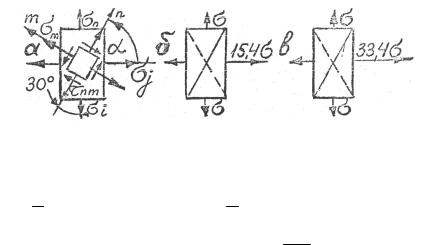
2.12. Из чертежа (рис.

2.36, а)

имеем,

что α = 60D , тогда

cos 2α = cos120 = −0,5 .

По

формуле

(2.6)

σn (σm ) =

=

σj + σi

±

σj

−σi

(−0,5), откуда

2

2

σj + 3σi

σ

n

=

.

(*)

σm

3σj + σi

Из условия задачи εn =

1

(σn

−μσm )= 0 , получим, что

σn

=μ; и,

σj

E

σm

обозначая

= k , из формулы (*) k =

3 −μ

.

σi

3μ −1

3 −0,39

Для сплава ниобия

k =

=15, 4 ,

т.е. если

σ = σ, то

3 0,39 −1

i

σj =15, 4σ (рис. 2.36, б).

Для чугуна k =

3 −0,36

=

33, 4 , т.е. если σ = σ, то σ

j

= 33, 4σ

3 0,36 −1

i

(рис. 2.36, в).

Рис. 2.36

2.13. Одноосная деформация будет в том случае, если εx ≠ 0 ,

εy = E1 σy −μ(σz + σx ) = 0 ; εz = E1 σz −μ(σx + σy ) = 0 . Выра-

жая σy , σz через σx , получим σy = σz = σx 1 −μμ .

86

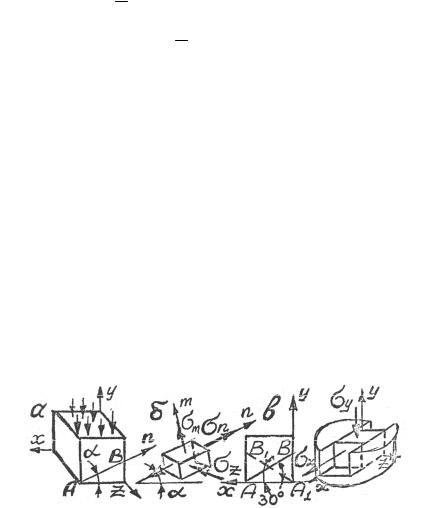
2.14.1. На верхней грани кубика σy = −p , а на свободной грани

σx = 0 . Из условия деформирования кубика имеем, что

εy = E1 (σy −μσz )= − δa = −3(1 −μ2 ) 10−4 ,

εz = E1 (σz −μσy )= 0 ,

откуда σy = −60 МПа, т.е. p = 60 МПа, а σz = − 15 МПа, так как

σz = μσy .

2. Найдем по формуле (2.6) нормальные напряжения, действующие вдоль волокна АВ и перпендикулярно ему и лежащие в

плоскости xy (рис. 2.37,

а,

б):

σn (σm )=

σx + σy

±

σx −σy

cos 2α,

2

σy

σy

2

откуда σn =

(1 −cos 2α),

σm

=

(1 + cos 2α).

2

2

1

3. По условию εn =

σn −μ(σm +σz ) = 0 ;

выражая все на-

E

пряжения через σy , получим 1 −μ −2μ2 −cos 2α −μcos 2α = 0. То-

гда cos 2α =	1 −μ − 2μ2	= 0,5 α = 30D (рис. 2.37, в).
	1 +μ
		εAB = εA B = 0 !
		1	1

Рис. 2.37

Рис. 2.38

87

	2.15. По условию задачи σy = −p , σx =	P	= 3 p (рис. 2.38).
		a2

Пользуясь обычной схемой решения предыдущих задач, из условия

деформирования	εz =	1	σz −μ(σx + σy )		= 0 , откуда σz =
		E

= 2μ p . Результат «парадоксальный», так как σz > 0 , т.е. растяги-

вающее. Это возможно только в том случае, если боковая грань кубика прикреплена (приклеена, приварена) к боковой стенке паза плиты, чего нет. Таким образом, предпосылка, что εz = 0 , ошибоч-

на. Это подтверждается определением деформации ребра z кубика

отдельно

от

действия σx

и σy :

az (σx ) = −μ

σx

a = −3μ

p

a ,

σy

E

E

az (σy )

= −μ

a = μ

p

a ,

откуда

суммарная деформация

ребра

E

E

равна −2μ EP a , т.е. ребро укорачивается, между стенкой паза и ку-

биком образуется зазор величиной 2μ EP a , напряжение σz = 0 , а

сам кубик испытывает двухосное напряженное состояние. Изменение размеров ребер кубика определим из

ε x=

ax

=

1

(σx −μσy )=

p

(3 +μ);

a

E

E

ε y =

ay

=

1

(σy −μσx )= −

p

(1 −3μ);

E

a

E

ε z =

az =

1

0 −μ(σx + σy )

= −2μ

p

.

a

E

2P

E

P

2.16. 1. Из условия задачи

σy (A)

= −

,

σy (B)= −

,

a2

a2

σy (C ) = 0 . σx (A) = σx (B) = σx (C ) = σx !

2. Запишем дополнительные уравнения из условия деформирования:

ε z(A)= E1 σz (A)−μ(σx + σy (A)) = 0 ;

88

ε z(B)=		1			σz (B)−μ(σx + σy (B))	= 0 ;
		E
ε z(C )=		1			σz (C )−μ(σx +σy (C ))	= 0 ;
		E

	a = a x(A)+ a x(B)+			a x(C ) ,		(*)
где	ax (i)= a ε x(i )=	a	σx −μ (σy (i)+σz (i ))		, при i = A, B, C.
		E			σz (A) ,	σz (B) ,
Решая совместно уравнения п.2, найдем				σx ,
σz (C ).

Обращаем внимание на часто совершаемую грубую ошибку, когда четвертое уравнение (*) представляют в виде

ε x(A)+ ε x(B)+ ε x(C )= 3aa !

2.17. Силу определим через напряжение на верхней грани:

P = σy a2 . Напряжение σy , как и σx , σz

найдем из совместных

решений дополнительных уравнений: ε z =

1

σz −μ(σx + σy )

= 0,

1

3 a

1

E

a

ε y =

= −

,

ε x=

=

.

E

σy −μ(σz

+ σx )

a

E

[σx − μ(σy + σz )

a

3

a

Обращаем внимание на знак «–» перед величиной

.

a

P

2.18. Вариант 1.

1.

Только

от

действия силы

P: σx

= −

,

F

P

μ

σy (P)= σz (P)= −

. Тогда смещение крышки по направле-

F (1 −μ)

нию оси x будет:

P (1 − 2μ)l (1 +μ)

ux (P)= εx l = l

1

σx −μ(σy (P)+ σz (P)) = −

.

E

EF (1 −μ)

89

. Тогда:

2. Только от действия температуры: σx (t ) = 0 , из условия де-

формирования ε y(t )= εz (t )= E1 σy (t )−μ(σz (t )+ σx (t )) + +α t = 0 , откуда σy (t )= σz (t )= −α1 −t μE

ux (t )= εx (t ) l = l E1 σx (t )−μ(σy (t )+σz (t )) = 11+−μμ α t .

3. С учетом суммарного действия P и t крышка поднимется на
ux = ux (t )−		ux (P)		1		+ μ		P (1 − 2μ)
			=				l α t −		.
				1		− μ		EF

Вариант 2. Учитываем как действие силы, так и действие тем-

пературы одновременно. При этом σx = − FP ; из условия деформирования ε y = εz = E1 σy −μ(σz + σx ) + αt = 0 , откуда

σy = σz = −

Pμ

−

α t E .

F (1 −μ)

1 −μ

Крышка поднимется на:

P (1 −2μ)

1

σx −μ(σy + σz )

1 +μ

ux= εx l =l

+αt

=

l

α t −

.

1−μ

EF

E

2.19. 1. Отнесем брусок к координатным осям x, y, z (рис. 2.39, а). Из уравнения равновесия ∑x = 0 : RA − RD = 0 , сле-

дует, что задача один раз статически неопределимая. На участке

ВС: σy = −p , σz = −p .

2. Для эквивалентной системы (рис. 2.39, б) дополнительное

	уравнение будет	иметь вид:	ux (D)= uxP (D)−uxRD (D)= 0 .
	uxp (D)= uxp (C )= ∫	l		1	σx −μ(σy +σz )
		εxdx = ∫εxdx ,	где ε x=				=
	LBC	0		E

90