Исаченко Сопротивление материалов ч.1 2010

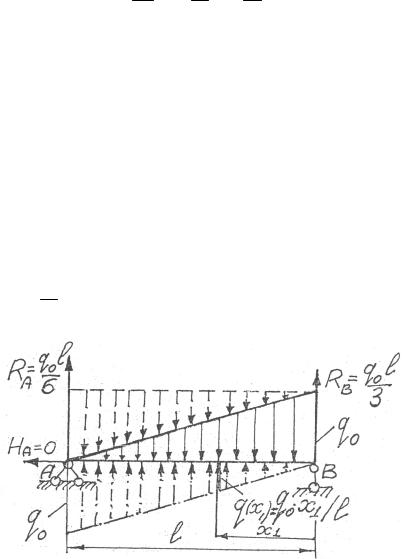
= q30l x1 − q20 x12 + q60l x13 .

2-й прием. Нагрузку на длине x1 разбиваем на две грузовые площади – треугольники Bcd и BdK . Тогда

						1							1									q	0		l											q	0	x2
Q	y	= −R		B	+		q(x		) x +					q		0	x			= −							+ q			0	x		−					1	,
						2							2									3															2l
							1			1								1														1
		M	z	= R		B	x −				q(x		)	x				1		x		−		1		q		0	x				2	x			=
									2									3					2
							1					1				1				1										1		3			1
							=	q0l				x −			q0		x2			+	q0		x3 .
																					6l
									3			1				2		1									1

3-й прием (рис. 4.19). Нагрузку по треугольнику при q < 0 достраиваем до нагрузки равномерно распределенной по длине интенсивностью q0 = const < 0 (штриховая линия); достроенную нагрузку уравновешивают треугольной нагрузкой q > 0 (штрихпунктир), с интенсивностью в сечении А q = q0 > 0 . Тогда

q(x1) = ql0 x1 .

Рис. 4.19

171

												1						q l									q x2
		Q		y	= −R		+ q		x		−			q(x ) x		= −		0		+ q				x	−		0 1		,
						B		0	1			2			1 1			3					0	1			2l
																															x3
						q	0	x2			1					1			q		0	l				q	x2			q0
M	z	= R	B	x −				1		+		q(x			) x		x	=					x −				0 1	+			1	.
								2			2					3				3							2
					1									1	1		1							1							6l

П р и м е р 7

Построим эпюры для балки, загруженной неравномерной распределенной нагрузкой (рис. 4.20).

I операция. Изображение расчетной схемы (см. рис. 4.20, а).

Рис. 4.20

172

II операция. Определение опорных реакций. Разбиваем всю распределенную нагрузку на равномерно распределенную с интенсивностью q0 и на нагрузку в виде треугольника со значением ин-

тенсивности в сечении на опоре А q = 2q0 . Равномерно распределенную заменяем ее равнодействующей, равной q0 l и приложенной посередине длины l, а распределенную по треугольнику заме-

няем равнодействующей, равной 12 2q0 l и приложенной в цен-

тре тяжести грузовой площади в виде треугольника, т.е. на рас-

стоянии	1	l	от опоры А.
3
Составляем уравнения равновесия:
∑X = 0			H A = 0 ;

∑mB = 0 RA l − 12 2q0 l 23 l − q0 l 2l = 0

RA = 76 q0 l ;

∑mA = 0 − RB l + q0 l 2l + 12 2q0 l 13 l = 0

RB = 56 q0 l .

Проверка:

∑Y = 0

RA −

3q0 + q0

l + RB = 0 0 ≡ 0 .

2

Выносим значение реакций на расчетную схему.

III операция. Составление выражений для Qy

и построение

эпюры Qy .

Qy

= −RB + q0 x +

1

q(x) x = −

5

q0 l + q0

x +

q0

x

2

,

(*)

2

6

l

q(x)

2q0

2q0

где q(x)

определено из соотношения

=

q(x) =

x .

l

x

l

Эпюра Qy ограничена кривой второго порядка.

173

При x = 0 Qy = −RB = − 56 q0l , при x = l Qy = RA = 76 q0l .

Приравняв выражение (*) к нулю, найдем значение абсциссы x0 , при котором Qy переходит через нуль. Квадратное уравнение

(*) дает два корня: x1 = 0,54l , x2 = −1,54l . Откуда следует

x0 = 0,54l .

Эпюра Qy изображена на рис.4.20, б.

Для определения знака кривизны линии, ограничивающей эпюру Qy , воспользуемся положением 4.3.7А.

Равномерно распределенная нагрузка интенсивностью q0 дает Qy , изменяющуюся по линейному закону. Кривизну линии, ограничивающей эпюру Qy , дает нагрузка с грузовой площадью в виде треугольника. В этой нагрузке интенсивность над опорой В равна нулю и, следовательно, tgα*B = 0 , α*B = 0 , т.е. касательная к

эпюре в сечении В располагалась бы горизонтально, если была бы только нагрузка, распределенная по треугольнику, что и определяет направление кривизны. Как видно из рис.4.20, б, касательная в

сечении В проходит под углом α

B

, так как tgα

B

=

dQy

= −q .

dx

0

IV операция. Составление выражения для M z

и построение

эпюры M z .

x

1

1

5

q0

x2

q0

x3

M z = RB x − q0 x

−

q(x) x

x =

q0 l x

−

−

,

2

2

3

6

2

3l

при x = 0

M z

= 0 ,

при x0 = 0,54l

M z

= M z (max) = 0,252q0 l 2 ,

при x = l

M z

= 0 .

Эпюра M z изображена на рис. 4.20, в. Кривизна линии, ограничивающей эпюру M z , определена, исходя из положения 4.3.7А и

4.3.7Б.

174

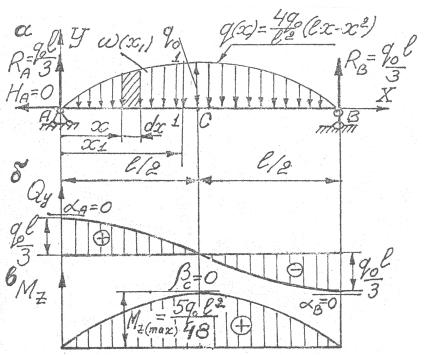
П р и м е р 8 (рис.4.21)

Построение эпюр Qy и M z покажем с использованием двух

разных приемов.

Прием первый – традиционный.

I операция. Составление расчетной схемы (см. рис. 4.21, а). II операция. Определение опорных реакций. Уравнение в ви-

де ∑X = 0 дает значение H A = 0 .

Рис. 4.21

Грузовая площадь ограничена симметричной квадратной параболой. В силу симметрии грузовой площади реакции RA = RB =

= ω/ 2 , где ω – грузовая площадь. Наибольшую высоту площади ω получим из условия, что при x1 = l / 2 q(l / 2) = q0 . Площадь, огра-

175

ниченная

выпуклой

параболой,

равна

ω=

2

h l =

2

q0 l . Тогда

3

3

q0l

RA = RB

=

– значения реакций,

которые выносим на расчет-

3

ную схему.

III операция. Составление выражения для Qy

и построение

эпюры Qy . Обозначим грузовую площадь,

лежащую слева от се-

чения 1 −1 через ω(x1 ) , тогда

Qy = RA − ω(x1) =

q0 l

x1

q0l

4q0

x1

x1

=

− ∫q(x) dx =

−

l ∫xdx − ∫x2 dx =

2

3

0

3

l

0

0

2

3

l

2x1

4x1

= q0

−

+

,

(1)

l

3l

2

3

при

x

= 0

Q

y

=

q0l

= R

A

,

1

3

l

при

x

=

Q

y

= 0 ,

1

2

q0l

при

x

= l

Q

y

= −

= R

B

.

1

3

Эпюра Qy

изображена на рис. 4.21, б. Обращаем внимание, что

касательные к линии,

ограничивающей эпюру Qy в сечении А и В,

горизонтальны, т.е. αA = 0 , αB = 0 , так как

q( A) =

dQy

= tgαA

= 0 и q(B) =

dQy

= tgαB = 0 ,

dx

dx

что и определило характер выпуклости линий, ограничивающих эпюру Qy .

IV операция. Составление выражений для M z и построение эпюры M z .

x1

M z = RA x1 − ∫q(x)(x1 − x)dx ,

0

176

где q(x)dx – элементарная сила, а (x1 − x) – плечо этой силы относительно сечения 1 −1.

Подставляя значение q(x)			и интегрируя, получим, что
					3			4
M z = q0	l x1			−	2x1	+	x1			,	(2)
			3		3l		3l	2

при x1

= 0

M z

= 0 ,

при x

=

l

M

z

= M

z

(max) =

5

q

0

l 2

,

48

1

2

при x1

= l

M z

= 0 .

Эпюра M z

изображена на рис. 4.21, в.

Прием второй, основанный на использовании дифференциальных зависимостей (4.4).

Qy = ∫[−q(x)] dx .

Обращаем внимание на знак минус в подынтегральном выражении, его наличие определено тем, что распределенная нагрузка действует вниз, т.е. q(x) < 0 !

Подставим заданное значение q(x) и проинтегрируем:

	− 4q0				2														2			x	3
Qy =			∫(lx − x			) dx = −						4q0 lx								−					+ C1	,
	l	2										l	2					2				3
				4q			0	lx3					x4
M z = ∫Qy dx = −											−							+ C1			x + C2 .
					l	2							12
								6

На концевых шарнирных опорах изгибающие моменты равны

нулю (см. положение 4.3.9). Таким образом,
при x = 0	M z		= 0 C2 = 0 ,
при x = l	M	z	= 0 = −	4q0 l 4		+	4q0 l 4	+ C l , откуда
				6l 2			12l 2	1

C1 = q03 l .

177

Тогда

l

2x2

4x3

Q

y

= q

−

+

,

2

0

3

l

3l

l x

2x3

x4

M

z

= q

0

−

+

,

3

3l

3l

2

что совпадает с выражением (1) и (2) при решении задачи традиционным путем.

П р и м е р 9 (рис. 4.22)

Для построения эпюр Qy и M z воспользуемся приемом, основанным на использовании дифференциальных зависимостей (4.4).

∫

∫

l

Qy =

[−q(x)] dx = −q0

sin

2πx

dx

=

=

l

q

0

cos

2πx

+ C

,

2π

l

l 2 q

1

l

2πx

0

2πx

M z = ∫Qy dx =

q0 ∫cos

dx =

sin

+ C1

x + C2 .

2π

l

4π2

l

Согласно положению 4.3.11

при x = l

Qy = 0

C1 = −q0l / 2π,

M z

= 0 C2

=

q0l 2

.

q0l

2π

2πx

q0l

Тогда Qy =

cos

−

,

2π

l

2π

при x = 0

Qy = 0 ,

при x = l / 2

Qy =

q0l

,

π

при x = l

Qy = 0 .

Эпюра Qy изображена на рис. 4.22, б. Обращаем внимание, что в сечениях А, В, С касательные к линии, ограничивающей эпюру

178

Qy , горизонтальны, так как αA = αB = αC = 0 , исходя из дифференциальной зависимости q A,B,C = dQdxy = tgαA,B,C = 0 .

Рис. 4.22

Подставляя значения постоянных C1 и C2 в выражениях для изгибающего момента, получим

M z =

q0 l 2

sin

2πx

−

q0

lx

+

q0

l 2

,

4π2

l

2π

2π

при x = 0

M z =

q0l 2

,

2π

179

	при x = l / 2	M z =	ql	2	,
			4l
	при x = l	M z = 0 .

Эпюра M z изображена на рис. 4.22, в. Обращаем внимание, что

	в сечениях А, В касательные к линии,					ограничивающей эпюру M z ,
	горизонтальны, так как βA =βB = 0 ,					исходя из дифференциальной
	зависимости (4.4) Qy ( A, B) =			dM z	= tgβA,B = 0 .
				dx
		В заделке А горизонтальная реакция H A = 0 , что следует из урав-
	нения		равновесия в виде	∑X = 0 . Вертикальная реакция
	RA = Qy ( A) = 0 . Опорный момент в					заделке А M A = M z ( A) =
	=	q0l 2	и направлен по часовой стрелке, как показано на рис. 4.22, а,
		2π

с тем, чтобы вызвать в сечении заделки (в балке правее заделки) положительный изгибающий момент («вода не сливается»!).

П р и м е р 10 (рис. 4.23)

Построить эпюры Qy и M z для балки, загруженной равномер-

но распределенными моментами, интенсивностью m Нмм .

I операция. Изображение расчетной схемы (рис. 4.23, а).

II операция. Определение опорных реакций. Составим урав-

нения равновесия:

∑X = 0 − H A = 0 ;

∑mB = 0 − RA l + m l = 0 RA = m ;

∑mA = 0 − RB l + m l = 0 RA = m .

Проверка:

∑Y = 0 − RA + RB = 0 0 ≡ 0 .

Выносим значения реакций на расчетную схему.

180