Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

ходное определение Ж. Лиувилля, предложенное им в работе 1832 г., основано на формуле дифференцирования показательной функции и относится только к функциям f x , представимым в виде

следующего ряда: f x Ck eak x . Для таких функций, согласно

k 0

определению Ж. Лиувилля, для производной любого (в том числе и комплексного) порядка p справедливо следующее соотношение:

Dp f x Ck ak p eak x . k 0

Ограниченность этого определения связана, очевидно, со сходимостью ряда, в виде которого представима рассматриваемая функция. В одной из работ Ж. Лиувилль получил также формулу дифференцирования дробного порядка для степенной функции. Более того, в той же работе Ж. Лиувилль выводит1 формулу

		1
p					p 1
D	f x		0	x t t	dt, x , ,Re p 0,
		1 p p

называемую теперь (без множителя 1 p ) лиувиллевой формулой

дробного интегрирования2.

В один ряд с работами Ж. Лиувилля по значимости следует поставить работы Б. Римана и Х. Хольмгрена. Работа Б. Римана по данному направлению, выполненная им в 1847 г. в студенческие годы, была опубликована только в 1876 г. – спустя десять лет после его смерти. Б. Риман пришел к следующей конструкции дробного интегрирования:

1	x t
	0		dt, x 0,
		x t 1

служащей с тех пор наряду с конструкцией Ж. Лиувилля одной из основных форм интегрирования дробного порядка.

1Однако необходимо отметить, что данный вывод представляется не совсем строгим с современной точки зрения.

2Здесь p – гамма-функция, определение которой приведено ниже.

88

На этом представляется оправданным, в рамках данной работы, закончить историческую справку, подойдя к возможности более подробного рассмотрения вопросов, связанных с дробным интегродифференциальным исчислением. Для более подробного знакомства с историческими аспектами интегродифференциального исчисления дробных порядков читателю можно посоветовать обратиться к [79, 80], где данный вопрос освещен детально.

§5. Интегральное уравнение Абеля

Понятие дробного интегрирования тесно связано с интегральными уравнениями Абеля. Необходимо отметить, что дробные интегралы и производные, так же как и интегральное уравнение Абеля и его обобщения имеют важное прикладное значение. Данный аппарат используется в самых различных областях прикладных исследований – в физике, механике, химии и др. После задачи Н. Абеля о таутохроне первые приложения аппарата дробного интегродифференциального исчисления к задачам геометрии, физики и механики были даны Ж. Лиувиллем. Среди рассмотренного круга задач была и задача Лапласа о влиянии прямолинейного проводника бесконечной длины на магнит; задача Ампера о взаимодействии двух таких проводников; задачи, связанные с притяжением тел; задача о распределении тепла в шаре; задача Гаусса о приближенных квадратурах и другие1.

5.1. Определение и решение уравнения Абеля

Определение 2.7. Интегральное уравнение

1	x	t		f x , x a,0 1
	a		dt		(2.8)
		x t 1

называется (интегральным) уравнением Абеля.

Для дальнейшего рассмотрения необходимы некоторые дополнительные определения, которые приводятся ниже.

Определение 2.8. Равенство

1 Подробный обзор задач, рассмотренных Ж. Лиувиллем, см., например, в

[79 – 81].

89

b	x	b	b
dx f x, y dy		dy f x, y dx		(2.9)
a	a	a	y
называется равенством Дирихле.
Определение 2.9. Функция
	1
B z,w xz 1 1 x w 1 dx, Re z 0,Re w 0				(2.10)
	0

называется бэта-функцией (эйлеровым интегралом первого рода).

Определение 2.10. Функция

z xz 1e xdx, Re z 0	(2.11)
0

называется гамма-функцией (эйлеровым интегралом второго рода). Известно, что справедливо следующее соотношение для эйлеро-

вых интегралов:
B z,w	z w	.	(2.12)
	z w

В силу важности, ниже приведем подробно решение уравнения Абеля. В (2.8) можно сделать замену x на t, положить t s соот-

ветственно; далее, умножить обе части равенства (1.8) на x t

и проинтегрировать полученное выражение по t на отрезкахa, x , x a,b , считая, что a,b – числа и рассматривая уравнение

Абеля (1.8) на конечном отрезке a,b . В результате выполнения

указанных преобразований можно получить следующее интегральное равенство:

x	dt	t	s	ds x	f t	dt.
			1
a x t		a t s		a x t

Поменяв порядок интегрирования по формуле Дирихле (2.9) в левой части данного соотношения, можно получить равенство

x	x		dt		x	f t
s ds							dt.
		x t		1
a	s		t s		a	x t

Внутренний интеграл в левой части равенства можно вычислить после замены t s x s и использования формул для эйлеро-

90

вых интегралов (2.10) и (2.12). Таким образом, можно получить

x

dt

1

следующую цепочку равенств:

1 1 d

1

s

x t

t s

0

B ,1 1 . В результате выполненных преобразо-

ваний можно получить:

f t

x

1

x

s ds

dt.

(2.13)

x t

a

1 a

Отсюда, после дифференцирования можно получить равенство

x

1

d

x

f t

dt.

(2.14)

1 dx

a x t

Таким образом, если уравнение Абеля имеет решение, то это решение имеет вид (2.14) и, следовательно, единственно.

Важно отметить, что для простоты в (2.8) рассматривался случай 0 1. Случай 1 очевиден, а случай 1 сводится, вообще говоря, к рассмотренному подробно случаю 0 1 дифференцированием обеих частей в (2.8).

Совершенно аналогично приведенному выше решению уравнения Абеля (2.8), рассматривается уравнение Абеля вида

1

b

t

f x , x b,

x

dt

t x 1

но в данном случае вместо (2.14) при

0 1

получается сле-

дующая формула обращения:

f t

x

1

d

b

dt.

(2.15)

1 dx

x t x

Методом математической индукции доказывается следующая общая формула для n -кратного интеграла вида

x	x	1		x
dt t dt				x t n 1 t dt.	(2.16)
		n
a	a		1 ! a

n

В силу того, что n n 1 ! правой части (2.16) можно прида-

вать смысл и при нецелых значениях порядка интегрирования n.

91

5.2. Обоснование решения уравнения Абеля

В данном разделе более подробно выясняется, при каких условиях на функцию f x , стоящую в правой части (2.8), уравнение

Абеля действительно разрешимо. Для того чтобы сформулировать основную теорему, введем следующее обозначение:

f1 x

1

x

f t

a

dt.

1

x t

Справедливо следующее неравенство:

b

f1 x

1

b

f t

b t 1 dt.

dx

(2.17)

2

a

a

Докажем данное утверждение.

Действительно, справедливы следующие соотношения:

b

1

b

x

f t

1

b

x

f

t

f1 x

dx

dt

dx

dx

dt.

1

x t

1

x t

a

a

a

a

a

Поменяв порядок интегрирования в последнем выражении, можно получить следующую цепочку равенств:

b

b

f

t

b

1

b

1

dt

dx

1

f t

x

t

dt

1

a

t

x t

1 a

1

b

f t

b

t

1

1

dt

f t

b t 1

dt.

1 1

1

2

b t

a

a

Неравенство (2.17) доказано.

Для дальнейшего рассмотрения представляется необходимым напомнить некоторые определения из математического анализа.

Определение 2.11. Функция	f x называется абсолютно не-
прерывной на отрезке a,b , a b,	если для каждого 0 сущест-

вует 0 такое, что для любой конечной системы попарно непересекающихся отрезков ak ,bk a,b , k 1,2, ,n, удовлетво-

n

ряющей условию bk ak , справедливо неравенство

k 1

92

n

f bk f ak .

k 1

Класс всех абсолютно непрерывных на отрезке a,b функций

обозначается AC a,b .

Замечание. Известно, что класс AC a,b

совпадает с классом

первообразных от суммируемых по Лебегу функций:

x

b

f x AC a,b f x C t dt,

t

dt .

a

a

Определение 2.12. Говорят, что функция

f x , заданная на

отрезке a,b , удовлетворяет условию Гельдера (порядка

) на

отрезке a,b , если x1, x2 a,b справедливо неравенство:

f x1 f x2

A

x1 x2

,

где A – некоторая постоянная, параметр

называется «показа-

тель Гельдера».

Класс всех (вообще говоря, комплекснозначных) функций, удовлетворяющих на отрезке a,b условию Гельдера фиксирован-

ного порядка , обозначается как H H a,b .

Необходимо отметить, что здесь важность представляет только

случай 0 1, так как при условии	1 класс H a,b со-
держит только константы: f x const	на a,b .
Важно, что H1 a,b AC a,b ;	обратное утверждение не-
верно. Действительно, например, f x		AC a,b , но, с
	x a
		0 1, так как в
другой стороны, f x x a H1 a,b при
точке x a условие Гельдера не выполняется.

Через L1 a,b обозначается множество всех измеримых на отрезке a,b функций f x , вообще говоря, комплекснозначных,

для которых справедливы следующие соотношения:

93

b

b

f x

dx ,

f x

L1 a,b

f x

dx.

a

a

Из приведенного выше доказательства справедливости неравен-

ства (2.17) следует, что если f x L1 a,b , то справедливо: f1 x L1 a,b . Необходимо дополнительно заметить, что на множестве функций L1 a,b справедлива теорема Фубини о сме-

не порядка интегрирования.

Теорема 2.3. Интегральное уравнение Абеля (2.8) при 0 1

разрешимо на множестве функций L1 a,b тогда и только тогда,

когда f1 x AC a,b и f1 a 0. При выполнении данных

условий уравнение Абеля (2.8) имеет единственное решение, определяемое формулой (2.14).

Доказательство. На первом этапе доказывается необходимость.

Пусть уравнение Абеля (2.8) разрешимо в L1 a,b . Тогда спра-

ведливы все рассуждения, приведенные выше в п.5.1, при этом возможность перестановки интегрирования в равенстве Дирихле (2.9) обосновывается с помощью теоремы Фубини. Следовательно, справедливо соотношение (2.13). Откуда следует, что выполняются

условия f1 x AC a,b и f1 a 0. Необходимость доказа-

на.

На втором этапе доказывается достаточность. В силу выполне-

ния условия теоремы f1 x AC a,b справедливо следующее соотношение: f1' x df1 x 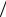dx L1 a,b . Поэтому функция

(2.14) существует почти всюду и принадлежит L1 a,b . Теперь

необходимо показать, что функция (2.14) действительно дает решение уравнения Абеля (2.8). Подставим функцию (2.14) в левую часть уравнения (2.8) и результат подстановки обозначим через g x . В результате данных преобразований можно получить сле-

дующее равенство:

94

1		x f1' t		dt g x .
		a			(2.18)
			x t 1
Доказав теперь, что почти всюду f x g x ,					тем самым будет

доказана достаточность, следовательно, и данная теорема. Равенство (2.18) есть уравнение Абеля (2.8) относительно функ-

ции f1' t . Данное уравнение заведомо разрешимо, поэтому, в

силу соотношения (2.14), справедливо следующее равенство:

f1' x	1			d	x g			t		dt,
	1 dx
					a x t
то есть f1' x g1' x .
Функции f1 x и g1 x		являются абсолютно непрерывны-

ми: первая по условию теоремы, вторая – в силу равенства (2.13) с функцией g x в правой части.

Тогда	f1 x g1 x C 1. По предположению теоремы спра-
ведливо	f1 a 0, а в силу того, что (2.18) – разрешимое уравне-
	1				a f1' t
ние справедливы равенства g a					a			dt 0. Поэтому
						a t 1
		x		f t g t
C 0. Таким образом, справедливо							dt 0. Последнее
		a		x t

равенство есть уравнение Абеля (2.8). В силу единственности решения уравнения (2.8) справедливо f x g x 0 на отрезке

a,b . Достаточность доказана. Теорема доказана. ▲

Необходимые и достаточные условия разрешимости интегрального уравнения Абеля были сформулированы выше в терминах

1 Необходимо отметить, что требование абсолютной непрерывности в данном рассуждении существенно: его нельзя ослабить просто до непрерывности, так как известны непрерывные функции, но не являющиеся абсолютно непрерывными, отличные от тождественной постоянной и имеющие почти всюду производную, равную нулю.

95

вспомогательной функции f1 x . Следующая лемма и следствие из нее дают простое достаточное условие разрешимости уравнения

Абеля в терминах самой функции

f x .

Лемма 2.1. Если

f x AC a,b ,

то и f1 x AC a,b и

при этом справедливо следующее равенство:

1

x

f1 x

f a x a 1 f '

t x t 1 dt .

(2.19)

2

a

Доказательство. Подставляя функцию

f t , представленную в

t

виде f t f a f ' s ds,

в следующее интегральное равенство

a

f t

f1 x

1

x

a

dt,

можно получить:

1

x t

f a

1

x

dt

t

f1 x

x a 1

f ' s ds.

(2.20)

2

1

a x t

a

Здесь первое слагаемое – абсолютно непрерывная функция, в силу

x

того, что x a 1

1 t a dt. Поскольку справедливо

a

x

dt

t

f '

x t

f '

s

(2.21)1

s

ds

ds dt,

a

x t

a

a a

x t

то второе слагаемое в (2.19) является первообразной от функции, соответствующей внутреннему интегралу в правой части (2.21), и, следовательно, абсолютно непрерывно. Представление (2.19) следует из (2.20) после перестановки порядка интегрирования. Лемма доказана. ▲

Следствие. Если f x AC a,b , то уравнение Абеля (2.8)

разрешимо при 0 1 на множестве функций L1 a,b , при этом решение (2.14) можно представить также в следующем виде:

1 Справедливость данного соотношения проверяется непосредственной перестановкой порядка интегрирования в обеих частях равенства.

96

1			f a		x f ' s
x							ds .	(2.22)
	1		x a		a x s

Действительно, условия разрешимости, сформулированные в теореме 2.3, выполнено в силу леммы 2.1 и формул (2.20) и (2.21). Так как x df1 x 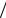dx , то формула (2.22) получается дифференци-

рованием равенства (2.19), при этом дифференцирование под знаком интеграла возможно в силу справедливости (2.21).

Совершенно аналогично представленной выше теореме 2.3 показывается, что уравнение

1	b	t		f x , x b
	x		dt
		t x 1

разрешимо на множестве функций L1 a,b для тех и только тех правых частей, для которых выполнена совокупность следующих

условий: f1 x AC a,b

и

f1 b 0, где при 0 1 функ-

ция f1 x

1

b f t

dt.

Решение

рассматриваемого

1

x t x

уравнения в случае

f x AC a,b

можно записать в виде

t

1

f b

b f ' s

ds .

1

b x

t s t

Необходимо отметить, что существует и другая форма обращения Абеля.

На основании изложенного выше, можно приступить к определению операторов дробного интегрирования и дифференцирования.

§6. Интегралы и производные во фрактальной геометрии

Как было показано выше (§5), аппарат дробного интегродифференциального исчисления известен в математике достаточно давно и к настоящему времени является хорошо разработанным и строго обоснованным [79, 81, 82]. Однако широкое применение дробных интегралов и производных в области релятивистской ядерной фи-

97