Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

bi s, x , зависящие от времени1. Таким образом, для неоднородных по времени случайных процессов уравнение (4.14) примет вид

p s, x,t, y

s

i j

(4.17)

n

2

p

n

p

i

1 aij s, x

bi s, x

s, x,t, y

s, x,t, y

2 i, j 1

x x

i 1

x

и уравнение (4.16) – следующий вид:

p s, x,t, y

t

(4.18)

2 aij t, y p s, x,t, y

bi t, y p

s, x,t, y

1

n

n

.

i

y

j

y

i

2 i, j 1

y

i 1

Уравнение (4.17) связано с дифференцированием по левому концу временного промежутка, уравнение (4.18) – соответственно, по правому концу временного интервала.

Важно отметить, что с точки зрения дифференциальных уравнений уравнение (4.17) означает, что плотность вероятностей перехода есть фундаментальное решение уравнения параболического типа

u		1	n	ij 2u				n	u
			a								0.
s					i	x	j		x	i
		2 i, j 1			x			i 1

Действительно, фундаментальным решением называется функ-

ция p s, x,t, y , s t, x, y Rn , удовлетворяющая при каждом фик-

сированном y уравнению (4.17), требованию регулярности того типа, что был указан выше в условии (4.13), стремящаяся к

y x	при s t, что можно сформулировать так: f Cфинит
	p s, x,t, y f y dy f x
	Rn
при s t.

1 При доказательстве данных теорем можно использовать сведение неоднородных марковских семейств к однородным.

198

Приведенное определение можно переформулировать следующим образом: фундаментальным решением является функция p s, x,t, y , при помощи которой возможно представление в виде

u s, x p s, x,t, y f y dy, s t

Rn

единственного ограниченного решения задачи Коши для рассматриваемого параболического уравнения с «конечным» условием ви-

да u t , x f x 1.

Уравнение (4.17) означает, что переходная плотность вероятностей является также фундаментальным решением уравнения вида

v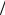 t L*v.

Важно отметить, что одна и та же функция p s, x,t, y является

фундаментальным решением различных уравнений. Однако данное обстоятельство не должно вызывать удивления: в теории дифференциальных уравнений тот факт, что одна и та же функция p s, x,t, y при изменении ее аргументов служит фундаменталь-

ным решением двух сопряженных друг другу параболических уравнений, хорошо известен.

Пример 4.10.

Свойство независимости приращений позволяет использовать винеровский процесс для построения любых диффузионных процессов. В данном случае уравнение Фоккера – Планка и обратное уравнение Колмогорова для переходных плотностей вероятности совпадают и сводятся к классическому уравнению диффузии:

p t, x, y a 2 p t, x, y .

2 x2

Переходная плотность одномерного винеровского процесса p t, x, y , являющаяся фундаментальным решением данного урав-

нения, определяется как

1 Здесь говорится именно о «конечном» условии, а не о начальном, так как уравнение вида u s Lu 0 решается «вниз», в отличие от уравнения вида u s Lu.

199

1				x y 2
p t, x, y			exp		.
		2 at		2at

Переходная плотность многомерного винеровского процесса подчиняется, соответственно, многомерному уравнению Фоккера –

Планка, имеющему следующий вид (при t0 0								и aij 1 ):
	p t, x, y	1			2
						p t, x, y		,
	t		2		y2
				i	i
фундаментальное решение которого имеет вид:
				n 2			y x 2
p t, x, y 2 t					exp
							2t

(см. также (3.23) выше).

Необходимо отметить, что уравнение Фоккера – Планка является частным случаем более общего уравнения Колмогорова – Чеп-

мена. Данное уравнение имеет следующий вид:
					P t1,t2				(4.19)
P t1,t3, x	, z	dyP t2	,t3, y	, z		, x	, y

и представляет собой уравнение для переходной функции марковского процесса, отражающее марковское свойство независимости будущего от прошлого при известном настоящем. Уравнение (4.19) может быть интерпретировано следующим образом. Вероятность перехода (переходная функция) из точки x при t1 в точку z в мо-

мент времени t3 равна переходной функции из точки x при t1 в

точку y в момент времени t2 , умноженной на вероятность перехо-

да переходной функции из точки y при t2 в точку z в момент времени t3 при всех возможных значениях y. Уравнение (4.19) может быть переписано и для соответствующих плотностей вероятностей.

Контрольные вопросы

1. Дайте определения марковского случайного процесса, марковского семейства.

200

2.Дайте определение диффузионного процесса. Приведите явный вид производящего оператора диффузионного процесса.

3.Приведите явный вид прямого и обратного уравнения Колмогорова.

4.Дайте формулировки теоремы 4.5 и 4.6 для обратной и прямой переходной плотности соответственно. Приведите доказательства данных теорем.

4.Приведите явный вид уравнения Колмогорова – Чепмена и поясните его смысл.

Рекомендуемая литература

4.1.Портенко Я.И., Скороходов А.В., Шуренков В.М. Марковские процессы. Итоги науки и техн. Современные

пробл. матем. Новейшие достижения. ВИНИТИ. 1989.

Т.46. С.5.

4.21. Холево А.С. Квантовое стохастическое исчисление. Итоги науки и техн. Современные пробл. матем. Новейшие достижения. ВИНИТИ. 1989. Т.36. С.3.

1 Данный обзор может использоваться в качестве введения в квантовое вероятностное исчисление.

201

Глава 5

БРОУНОВСКОЕ ДВИЖЕНИЕ

§1. Вводные замечания

С точки зрения физики для броуновского движения справедливо следующее определение

Определение 5.1. Процесс броуновского движения – это непрерывное хаотическое движение малых частиц (размерами в несколько микрометров и менее), взвешенных в жидкости или газе, происходящее под действием молекул (конституентов) окружающей среды.

Физическое явление, которое получило название «броуновское движение», впервые наблюдал шотландский биолог Р. Броун (1773

– 1859 г.г.), именем которого оно и было названо. Р. Броун в 1827 г. наблюдал в микроскоп движение цветочной пыльцы, взвешенной в воде, и описал наблюдаемый им эффект именно как физическое явление. Видимые лишь под микроскопом взвешенные частицы (броуновские) размером в несколько микрометров движутся независимо друг от друга, описывая сложные и сильно нерегулярные траектории. Наблюдаемое движение не ослабевает со временем, не зависит от химических свойств среды, его интенсивность увеличивается с ростом температуры среды и с уменьшением ее вязкости и размеров частиц. Качественное объяснение данного явления основывается на том факте, что взвешенная частица испытывает очень большое («бесчисленное») число столкновений со случайно движущимися молекулами окружающей жидкости; каждое отдельное столкновение оказывает пренебрежимо малое действие на частицу, но вместе они производят наблюдаемое движение. Таким образом, причиной броуновского движения является тепловое движение молекул среды и отсутствие точной компенсации ударов, испытываемых взвешенной частицей со стороны окружающих ее конституентов среды (молекул), то есть броуновское движение обусловлено флуктуациями давления. Удары молекул среды приводят броунов-

202

скую частицу в состояние хаотического непрерывного движения: скорость частицы быстро меняется по величине и направлению. Если фиксировать положение частицы через небольшие равные промежутки времени, то построенная таким методом траектория – броуновская кривая – оказывается исключительно сложной и запутанной (см. ниже).

Простейшей физической моделью броуновского движения является модель Эйнштейна – Смолуховского, созданная ими в 19051906 г.г. В рамках данной модели для была получена следующая формула:

x2 2Kd t,

называемая законом Эйнштейна. Здесь x2 – средний квадрат

проекции смещения броуновской частицы на некоторую ось, Kd – коэффициент диффузии, t – промежуток времени наблюдения. Формула Эйнштейна справедлива при условии, что данный временной промежуток достаточно велик, чтобы силы, действующие на частицу со стороны молекул среды, много раз поменяли свое направление. Для сферической частицы радиуса a коэффициент диффузии определяется на основе закона Стокса для гидродинамического сопротивления движению сферы заданного радиуса в вязкой жидкости и выражается формулой Kd kT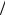6 a , где T – температура, – динамическая вязкость среды. Важно отметить,

что при выводе закона Эйнштейна помимо равновероятности смещения частицы в любом направлении пренебрегалось инерцией броуновской частицы по сравнению с влиянием сил вязкого трения (это допустимо только при достаточно больших t или в среде с большой вязкостью).

Кроме поступательного броуновского движения существует также вращательное броуновское движения, которое можно определить как хаотическое вращение броуновской частицы под влиянием ударов молекул среды. В рамках модели Эйнштейна – Смолуховского среднеквадратичное угловое смещение броуновской частицы определяется следующим образом:

2 2Kdврt,

203

где Kdвр – коэффициент диффузии для вращательного броуновского движения. При указанных выше допущениях для сферической частицы Kdвр kT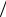8 a3 .

Опыты Ж.-Б. Перрена (1870 – 1942 г.г.) подтвердили справедливости представленных формул как для поступательного, так и для вращательного броуновского движений, хотя последний эффект наблюдать значительно сложнее, чем поступательное движение. Применив к наблюдаемому под микроскопом блужданию частиц закон больших чисел, Ж.-Б. Перрен сумел экспериментально оценить постоянную Больцмана k и число Авогадро NA . Ж.-Б.

Перрен в 1926 г. был удостоен Нобелевской премии за свою работу, посвященную броуновскому движению. Великий математик Н. Винер (1874 – 1964 г.г.) и его коллеги продолжили исследование броуновского движения частицы. В 1923 г. Н. Винеру удалось построить первую, удовлетворительную с математической точки зрения, модель вторичных реализаций и доказать свойство их «почти наверное» непрерывности.

Как известно, закономерности броуновского движения послужили наиболее наглядным экспериментальным подтверждением фундаментальных положений молекулярно-кинетической теории. Теория броуновского движения имеет принципиальное значение, она проясняет статистическую природу второго начала термодинамики и показывает границы его применимости.

Однако несмотря на солидный «возраст» открытия, многие сложные вопросы, связанные с броуновским движением, на протяжении многих лет оставались без ответа. В настоящее время броуновскому движению посвящена обширная литература. В рамках настоящей книги авторы используют работы [78, 123, 124, 126, 127], в которых дано более или менее строгое изложение данного вопроса.

§2. Линейное (одномерное) броуновское движение

В основе традиционного подхода к анализу случайных сигналов лежит спектрально-корреляционная теория. Однако за исключением только класса гауссовских процессов, полное статистическое описание случайных сигналов требует оценки моментов высших

204

порядков с учетом многоточечных корреляций. Резкое возрастание сложности и объема вычислений при ухудшении их точности ставит под сомнение само описание случайных процессов такими характеристиками. Альтернативный подход заключается в оценке фрактальных размерностей различных связанных с исследуемым процессом геометрических объектов. Распределения фрактального типа во времени и пространстве могут иметь плотности распределений случайных величин, графики сигналов, множества экстремумов случайных процессов и так далее.

Математической моделью одномерного броуновского движения, соответствующей физической модели Эйнштейна – Смолуховского, является винеровский процесс, который часто в литературе называется процессом броуновского движения. Одним из важнейших примеров случайного процесса, обладающего фрактальными свойствами, является именно классический процесс броуновского движения.

2.1. Дискретная аппроксимация

Простейшей дискретной аппроксимацией броуновского движения служит одномерное случайное блуждание. В данном случае

рассматриваемая	частица первоначально располагается в точке
x0 0 на прямой.	Частица совершает единичный шаг вправо или

влево в зависимости от случайного выбора, определяемого, например, бросанием монеты. Случайное блуждание происходит итеративно. Для каждого n 1,2,3, положим xn xn 1 1. Более точным приближением к реальному броуновскому движению является замена шагов величиной 1, шагами, величина которых является случайной величиной gn , имеющей гауссово (нормальное) распределение. После первого шага итерационной процедуры частица будет находиться в положении x1 x0 g1, а после n шагов, соот-

ветственно, – в положении xn xn 1 gn . На рис. 5.1 изображена типичная реализация гауссовского случайного блуждания.

Гауссовское случайное блуждание достаточно легко может быть реализовано с помощью компьютерного моделирования. Существует несколько способов генерирования случайных чисел, распре-

205

деленных по нормальному закону. В рамках одного из них используется генератор равномерно распределенных на отрезке 0,1 слу-

чайных чисел. Тогда из выборки k полученных случайных чи-

сел можно получить выборку нормально распределенных величин,

		12	n
	используя следующую формулу: gn		i 1 i		. Справедли-
				3n
		n

вость данной аппроксимации следует из применения центральной предельной теоремы.

Рис.5.1. График реализации одномерного гауссовского случайного блуждания. Для получения более реалистичного графика соседние точки соединены линиями

Определение 5.2. Гауссовский процесс называется одномерным броуновским движением или классическим винеровским процессом на отрезке a,b и обозначается B t , если он обладает сле-

дующими свойствами:

1)B 0 0 и функция B t почти всюду непрерывна на a,b ;

2)(свойство гауссовости приращений) t2 t1 случайная вели-

чина B B t2 B t1 имеет гауссово (нормальное) распределе-

ние с нулевым математическим ожиданием и дисперсией равной2 t2 t1 , где – положительная константа, то есть

P B x

1

x

u2

exp

du. (5.1)

2 2 t

t

2

2

t2

2

t1

1

206

В частном случае 1 процесс B t называется стандартным

процессом броуновского движения (или, как было указано выше в гл. 3, стандартным винеровским процессом). Необходимо отметить, что данный тип случайных процессов занимает центральное место в теории случайных процессов.

2.2. Основные свойства

Закон дисперсии и стационарность. Из свойства 2) определения

5.1 следует закон дисперсии для броуновского движения:

t1,t2 a,b : D B t2 B t1 2 t2 t1 .

Всилу того, что дисперсия зависит только от разности t2 и t1, а не

от самих значений, то говорят, что приращения в случае броуновского движения стационарны.

Свойство независимости приращений.

Броуновское движение обладает независимостью приращений в том смысле, что если 0 t1 t1' t2 t2' tk tk' 1, то прираще-

ния		'		,	j 1, ,k являются независимыми случайны-
	B tj B tj

ми величинами.

Необходимо отметить, что, как и случае винеровского процесса, существует несколько эквивалентных определений процесса броуновского движения. Например, указанное выше свойство независимости приращений включается непосредственно в определение, которое может быть сформулировано следующим, более развернутым, образом [128].

Определение 5.3. Стандартным процессом броуновского движения (стандартным винеровским процессом) называется случайный процесс Bt , t 0, удовлетворяющий следующим условиям:

1)	B0 0 почти наверное;
2)	если 0 t0 t1 tn , то приращения Bti 1 Bt , i 0, n 1
являются независимыми случайными величинами;
3)	s,t 0 приращение	B Bt s Bt распределено нормально
со средним 0 и дисперсией		s;

207