Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

ПРЕДИСЛОВИЕ

Использование современных математических методов и подходов нередко приводило к революционным изменениям в понимании и описании физической картины мира. В настоящее время в различных областях фундаментальной физики все более популярными становятся такие разделы математики, как фрактальная геометрия и фрактальные или недифференцируемые функции, случайные процессы и обобщенные устойчивые распределения. Аппарат указанных разделов математики успешно используется, в частности, в исследованиях по квантовой теории поля, физике высоких энергий, теории хаоса и критических явлений в квантовых системах. Применение понятий самоподобия и фрактальности оказалось полезным, в частности, для развития современных подходов в квантовой механике и в квантовой хромодинамике.

В рамках предлагаемого пособия авторы в явной форме постарались продемонстрировать глубокую взаимосвязь фрактальной геометрии и физики фундаментальных взаимодействий. В пособии изложены математические основы теории операторов дробного порядка, теории вероятностей и случайных процессов, необходимых при рассмотрении случайных фракталов. Рассмотрено применение данного математического аппарата для описания броуновского движения, в различных областях современной физики высоких энергий, а именно, в корреляционном анализе и при изучении распределений по множественности. Такой подход к изложению материала, по мнению авторов, является актуальным и представляется положительной отличительной чертой настоящего пособия. Данное пособие продолжает серию учебно-методических работ, посвященных фракталам в современной фундаментальной физике.

Пособие не претендует на обзор последних достижений ни в физике многочастичных процессов, ни в используемых разделах математики.

Авторы выражают глубокую благодарность профессору Сергееву Ф.М. за постоянный интерес к работе и многочисленные полезные обсуждения. Авторы искренне признательны Окорокову М.А. за предоставление необходимых компьютерных ресурсов и помощь в подготовке к изданию данного учебного пособия.

8

ВВЕДЕНИЕ

На наиболее фундаментальном уровне исследования в экспериментальной и теоретической физике высоких энергий представляют собой исследования природы массы и энергии и, в конечном счете, структуры и геометрии пространства-времени. В настоящее время одним из многообещающих подходов представляется исследование функциональных уравнений Шредингера и соответствующих формулировок принципа неопределенности для «квантовой механики струн». Важнейшим следствием в данном случае является введения квантового пространства-времени дробной размерности, то есть фрактального пространства-времени в квантовой физике. Роль фракталов и соответствующей геометрии в квантовой физике содержит два аспекта. Во-первых, само изучаемое пространство может обладать фрактальными свойствами и это может оказывать влияние на динамику квантовых систем. Одним из примеров здесь может служить явление перколяции. Во-вторых, рассматриваемое пространство может быть достаточно гладким, и проявление фрактальных свойств, фрактальной геометрии может быть обусловлено динамикой квантовой системы. Важнейшим примером в данном случае может служить интерпретация интегралов по траекториям Фейнмана и глубокая взаимосвязь броуновского движения и квантовой механики. Данный пример более подробно рассматривается ниже.

Важно отметить, что в отличие от конструктивных фракталов, рассмотренных в [1], более реалистичные фракталы для квантовой физики должны строиться и исследоваться с привлечением основополагающих для данной области исследований понятий: «вероятность» и «случайность». Таким образом, фракталы в квантовой физике являются, по своей сути, «случайными» или «вероятностными» фракталами.

Вероятность в квантовой физике – это категория, необходимость привлечения которой обусловлена тем, что наблюдаемое поведение физических объектов атомного и субатомного уровня носит выраженный статистический характер. Соответственно, предсказания квантовой теории, описывающей поведение микрообъектов, являются по своему существу вероятностными и выражаются в

9

терминах вероятностей переходов, средних значений, дисперсий, корреляций и так далее.

Принципиально важным, однако, является следующее обстоятельство: хотя результат каждого, отдельно взятого эксперимента можно рассматривать как обычную случайную величину, оказывается, что невозможно дать «классическое» описание совокупности статистических результатов всевозможных экспериментов над данным микрообъектом, которое характеризовало бы состояние этого микрообъекта в терминах какого-либо пространства элементарных исходов. Квантовая статистичность подлинна в том смысле, что носит первичный характер и принципиально неустранима за счет повышения точности и детальности измерений. С математической точки зрения это свойство квантовой теории выражается в том, что вероятностное описание квантово-механического объекта не может быть целиком построено на классической аксиоматике пространства элементарных исходов и требует привлечения иных аналитических средств. Такие методы разработаны в рамках, например, некоммутативной теории вероятностей.

Тезис о невозможности введения в квантовую механику «скрытых параметров», то есть о несводимости квантовых вероятностей к той или иной форме классического вероятностного описания был выдвинут Н. Бором и послужил предметом глубокой физикофилософской дискуссии в 30-х гг. XX века. Признание де факто такой несводимости явилось следующим после построения кинетической теории вещества принципиальным шагом на пути отказа от догматов детерминизма и внедрения статистических категорий в физическое мышление [2].

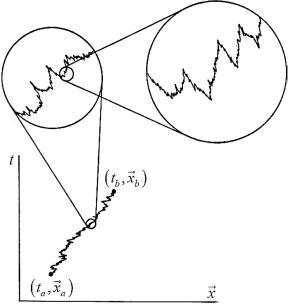
В 40-х годах XX века Р. Фейнманом была выдвинута гипотеза, согласно которой амплитуда вероятности перехода квантовомеханической системы из начального состояния с 4-мерной координатой ta , xa в конечное состояние с координатой tb , xb про-

порциональна сумме амплитуд, соответствующих всевозможным траекториям связывающим точки a и b. Данное предположение лежит в основе метода функционального интеграла, представляющего собой метод квантования физических систем, альтернативный волновой механике Шредингера и операторному методу Гейзенберга [3]. Необходимо отметить, что основы математической тео-

10

рии интегралов по траекториям были заложены в 20-х годах XX века Н. Винером, однако строгая математическая теория функциональных интегралов пока еще не создана. Представление амплитуды перехода в виде функционального интеграла естественным образом обобщается на случай квантовой теории поля (КТП). Данный метод занимает особое место в теории калибровочных полей. Необходимо отметить, что исторически первый пример использования геометрии сильнонерегулярных, сильноизрезанных объектов1 в квантовой физике был предложен Р. Фейнманом и А. Хиббсом в 1965 г. именно при рассмотрении самоподобного (фрактального) поведения контуров, возникающего в интегрировании по траекториям в КТП. В то время как частицы в классической механике двигаются по гладким (дифференцируемым) траекториям, в квантовой механике, как известно, ситуация отличается качественно. Как было отмечено в [4], в рамках фейнмановской интерпретации квантовой механики перемещения массивной частицы, которые условно можно описывать траекториями, в квантовой механике являются недифференцируемыми и самоподобными кривыми, то есть сильно изломанными зигзагообразными кривыми (рис. В.1). Необходимо отметить аналогию квантовой траектории с фрактальной кривой, которая имеет подобный вид на различных масштабах (см. рис.

В.1).

В связи с этим, еще в 1965 г. Р. Фейнманом и А. Хиббсом было особо отмечено свойство (стохастического, веротностного) самоподобия, которое играет исключительно важную роль во многих областях современной физики [4]. Затруднительно точно в количественном смысле определить, в чем именно состоит «нерегулярность» или «изрезанность» рассматриваемых объектов, не считая, конечно, отрицательной характеристики – это не многообразия и не счетные объединения таковых. Как было показано в [1], в настоящее время существует несколько определений понятия «фрактал», носящих, как правило, достаточно общий качественный характер. Важно отметить, что множество дробной хаусдорфовой размерности, очевидно, «нерегулярно», но оно не обязано быть «самоподоб-

1 Это соответствует фрактальной геометрии, однако в то время, когда появился данный пример, термины «фрактал», «фрактальная геометрия» еще не были введены.

11

ным», а множество целой хаусдорфовой размерности вполне может быть «нерегулярным» (или, можно сказать другими словами, «изрезанным») и при этом обладать или не обладать свойством локального «самоподобия». Не является вполне обязательным для фракталов и другое свойство, первоначально также называвшееся как основное: хаусдорфова размерность больше топологической [5]. Термин «фрактальный» можно трактовать и как «дробный, не целый», так и как «изломанный» [1, 6].

Рис. В.1. Типичная траектория квантовой частицы в фейнмановской формулировке, являющаяся сильнонерегулярной кривой на малых масштабах [4]. Данная кривая нигде не дифференцруема и стохастически самоподобна

В ряде случаев наблюдения о «фрактальности» тех или иных множеств (включая сюда утверждения и о размерности, и о «самоподобии») подтвердились в ходе строгих математических исследований, при этом был достигнут значительный прогресс и в других отношениях. Это особенно относится к «конформной динамике», то есть исследованию итераций аналитических функций в области комплексного переменного [2].

12

В классической физике недифференцируемой траекторией обладает броуновская частица. Траектория броуновской частицы является одним из наиболее известных и важных примеров фрактальных кривых.

Броуновское движение играет особую роль в квантовой физике. Функциональный или континуальный интеграл, предложенный Р. Фейнманом, является обобщением интегралов по траекториям, введенных в работах А. Эйнштейна и М. Смолуховского и применяемых при изучении броуновского движения в классической физике. Как было указано выше, стандартная формулировка и интерпретация квантовой механики базируется на теории вероятностей, при этом считается, что волновая функция (ВФ) системы покрывает все конфигурационное пространство, описывая вероятность локализации системы в определенной точке пространства-времени. Однако такая интерпретация не обеспечивает интуитивно понятной картины явлений микромира, какую дает, например, классическая механика для явлений макромира. Вследствие этого были предложены альтернативные интерпретации и формулировки, основанные на интуитивно более понятной концепции траектории. Одной из формулировок такого рода является рассмотренная выше фейнмановская формулировка квантовой механики. Основой другого подхода является теория квантового броуновского движения [7]. Было показано [7, 8], что имеется тесная взаимосвязь между броуновским движением и квантовой механикой1. Броуновское движение переходит в свободное движение массивной квантово-механической частицы, если выполняются формальные замены времени t it и

коэффициента диффузии Kd 2m, при этом уравнение диффузии переходит в уравнение Шредингера нерелятивистской квантовой механики. В [9] было показано, что усредненная квантовомеханическая траектория свободного движения обладает фрак-

тальной	геометрией с целочисленной размерностью Хаусдорфа
dH 2.	Таким образом, динамика свободной системы без гранич-

ных условий может быть охарактеризована на основе фрактальных

1 Подробное рассмотрение данного вопроса может служить предметом отдельной книги. В данном пособии рассматривается только соответствующий математический аппарат.

13

траекторий. Контуры для большинства взаимодействий (с локальными потенциалами) соответствуют траекториям с размерностью Хаусдорфа dH 2. Интерес представляют ситуации, когда dH 2. Пример такой ситуации – потенциал, зависящий от скорости, U x4 , который может встретиться, когда частица распространяется в среде, приводя в результате к модифицированным дисперсионным соотношениям. В качестве другого примера можно было бы рассмотреть квантовую механику в искривленном пространствевремени, соответствующем ситуации, когда квантовая частица падает на нейтронную звезду или черную дыру [10].

Особую роль при исследовании основ квантовой механики играют так называемые квантовые фракталы. Данные объекты, например, позволяют снять некоторые противоречия в квантовой механике Бома [11, 12], сохраняя всю ее предсказательную силу и интуитивно более понятную формулировку на основе сильноизрезанных нигде не дифференцируемых траекторий. При этом квантовые фракталы рассматриваются как волновые функции, у которых реальная и мнимая части являются всюду непрерывными, но нигде не дифференцируемыми функциями. В данном подходе квантовые траектории, ассоциированные с указанными ВФ, также являются фракталами [13]. Важно отметить, что в настоящее время исследования в данной области продолжаются.

В системах многих тел таких, как системы спинов или системы полей в КТП, фрактальная геометрия оказывается полезным инструментом, в особенности для анализа критических явлений. Используя ковры Серпинского, оказалось возможным моделировать системы в пространстве нецелого числа измерений и изучать критическое поведение как функции размерности пространства. Выполнение численных моделирований методом Монте-Карло на таких решетках дает информацию в непертурбативной области теории при нецелом числе измерений. Фрактальная геометрия использовалась для анализа геометрии критических кластеров при фазовых переходах второго рода. Интересным и важным является вопрос соотношения между критическими показателями и хаусдорфовой размерностью. Однако, к сожалению, нет никакого уникального пути для определения такой хаусдорфовой размерности. В квантовой гравитации, например, размерность Хаусдорфа была оп-

14

ределена через сравнение масштабных показателей для двух наблюдаемых, которые имеют естественные физические размерности длины и объема соответственно. Размерность Хаусдорфа, определенная таким способом, тесно связана с аномальной размерностью вершинной функции [10].

В настоящее время значительные усилия, в частности, в физике фундаментальных взаимодействий концентрируются на изучении так называемых квантовых фазовых переходов или квантовых критических явлений. Действующие экспериментальные установки на коллайдере релятивистских тяжелых ионов (RHIC) Брукхейвенской национальной лаборатории, экспериментальная программа на на- учно-ускорительном комплексе LHC (CERN) позволяют исследовать сильновзаимодействующую материю при экстремально высоких температурах и плотностях энергии. Особый интерес представляет фазовый переход от состояния деконфайнмента к состоянию бесцветной адронной материи. Важно отметить, что в настоящее время интенсивно развиваются как теоретические, так и экспериментальные исследования в новой области физики фундаментальных взаимодействий, которую можно назвать «релятивистская ядерная физика конденсированных / сплошных сред». Таким образом, рассматриваемые в данной книге методы могут носить важный междисциплинарный характер.

Один из наиболее интересных аспектов – это роль фрактальной геометрии при фазовом переходе к состоянию деконфайнмента при конечной температуре в теории поля на решетке. Была найдена наблюдаемая (токовая петля монополя), которая является нефрактальной в фазе деконфайнмента, но становится фрактальной в фазе конфайнмента. Таким образом, данная наблюдаемая характеристика играет роль параметра порядка [10].

Делаются попытки описания поведения кварков тяжелых ароматов в окружающей среде на основе классического броуновского движения [14]. При этом окружающая среда может рассматриваться в качестве сильнонерегулярного фрактального пространства. Известно, что в макрофизике при изучении процесса просачивания именно фрактальная геометрия является подходящей для описания геометрии пористых сред. Таким образом, математический аппарат, разработанный для описания транспортных явлений во фрактальных пространствах, может оказаться полезным при построении

15

более реалистичных моделей в релятивистской ядерной физике. При моделировании таких важнейших коллективных эффектов как азимутальные корреляции относительно плоскости реакций может быть полезно уравнение Ланжевена. Применение простейшего варианта данного уравнения позволило разумно на качественном уровне описать параметр эллиптического потока в столкновениях релятивистских тяжелых ионов при энергиях RHIC [15, 16]. Однако в настоящее время в распоряжении физиков имеется мощный математический аппарат, позволяющий выполнять обобщения стандартного уравнения Ланжевена для моделирования сложных статистических физических явлений. Важно отметить, что в связи с выполнением и планированием экспериментов с пучками тяжелых ионов при релятивистских энергиях в условиях больших множественностей вторичных частиц использование рассматриваемого в данной книге математического аппарата будет находить все более широкое применение в релятивистской ядерной физике как для экспериментальных исследований новых состояний сильновзаимодействующей материи в экстремальных состояниях, так и для построения более реалистичных феноменологических моделей.

Важно отметить, что в основе указанных выше физических мо-

делей и подходов лежит глубокая математическая теория: со-

временная теория вероятностей, теория операторов дробного порядка и фрактальных функций, фрактальная геометрия.

Врезультате ряда исследований было обнаружено исключительно важное соответствие между фракталом, являющимся геометрическим объектом, который обладает свойством самоподобия,

иренормализационной группой в физике, которая также была построена с учетом свойства самоподобия (приводя к возникновению бегущей константы взаимодействия).

Внастоящее время физика адронных процессов часто сводится к исследованию струй адронов, изучение свойств которых позволило получить ряд экспериментальных подтверждений справедливости предсказаний КХД. Одним из важнейших модельно независимых предсказаний КХД является зависимость сечения взаимодействия партонной конфигурации от ее геометрии. Таким образом, исследование геометрических характеристик конечных адронных состояний может помочь существенно продвинуться в понимании динамики процессов сильного взаимодействия и, в конечном

16

итоге, затрагивает фундаментальные вопросы о структуре про- странства-времени и физическом смысле геометрии. Как известно, фрактальная размерность в классической физике дает некоторую информацию о поведении наблюдаемой (например, длины береговой линии), когда разрешение по длине стремится к нулю [1]. Подобная ситуация возникает, когда рассматриваются адронные структурные функции в зависимости от квадрата переданного импульса, для которого обратная величина может трактоваться как квадрат длины волны, определяющей пространственное разрешение. Необходимо отметить, что структурные функции являются важнейшим элементом, характеризующим начальное состояние при описания процесса образования адронных струй.

Таким образом, по-видимому, наряду с объектами, форма которых с высокой степенью точности изображается привычными «евклидовыми» фигурами, в природе действительно встречаются объекты «фрактальной» формы. Важно отметить, что пока это только феноменология: встает вопрос, почему тот или иной объект имеет фрактальную форму, и притом с такими-то количественными характеристиками.

Вданной книге рассмотрен ряд областей именно квантовой физики, в которых фрактальная геометрия играет существенную роль.

Краткое содержание данного пособия следующее.

Впервой главе рассматриваются процессы глубоко неупругого рассеяния и адронные структурные функции. Основное внимание уделено зависимостям физических характеристик от квадрата переданного импульса. Показана роль, которую фрактальная геометрия могла бы, возможно, играть при изучении внутренней структуры частиц. Актуальность данного подхода обусловлена как современными прецизионными экспериментальными результатами, полученными при изучении структуры протона на RHIC, так и планируемым развитием данной области исследований и, в частности, проектом создания электрон-ядерного коллайдера (e-RHIC).

Вследующих трех главах вводится математический аппарат, необходимый для исследования как самих случайных фракталов, так и физических процессов, происходящих в пространствах с соответствующей нетривиальной структурой. Подробно рассмотрено интегро-дифференциальное исчисление дробных порядков, аксиоматический подход в теории вероятностей и случайные процессы.

17