Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

1

n

2

f

x

yi xi y j x j

y x

2

P t, x,dy .

i

j

2

i, j 1

x x

Первый интеграл в правой части полученного равенства в силу

условия					(4.11а) теоремы оценивается по модулю величиной
2		f x					t и при малых t 0 он не превосходит k ; k	– конеч-
					o
ный множитель (то есть нескольких ). В силу того, что								можно

взять сколь угодно малым, то получается, что данное слагаемое равномерно стремится к нулю при t 0.

В силу условий теоремы (4.11б) и (4.11в) второй интеграл будет

n

f x

1

n

2

f x

равен

bi x t

aij

x t

t и

плюс слагае-

o

i

i j

i 1

x

2 i, j 1

x x

n

2

n

мое,

не превосходящее

величины

aij x t o

t

при

2 i, j 1

t 0

t 0.

В силу выбора n данное слагаемое будет отличаться от про-

t Lf x

f x

изведения

менее,

чем на величину t n max

xi

i

n2

2 f x

n2

n

ii

n3

max

a

.

i

x

j

2

2 i, j

x

i

2

f Cфинит2 ,

Таким образом,

f DL Lf x Lf x ,

где DL

– об-

ласть задания оператора L.

Теорема доказана. ▲

Следствие. Если сделать траектории рассматриваемого марковского семейства непрерывными, то в условиях теоремы 4.3 t ,Px

оказывается диффузионным процессом.

Важно отметить, что условия теоремы 4.3 являются слишком ограничительными, жесткими. Как утверждал А. Вентцель, настолько ограничительными, что ему не удалось привести красивого или интересного с точки зрения реальных приложений примера, удовлетворяющего условиям данной теоремы, кроме винеровского процесса [125].

188

Из условий теоремы 4.3 вытекает, что коэффициенты aij x и

bi x ограничены во всем пространстве1.

Указанные выше условия теоремы 4.3 можно сделать более мягкими, если ограничиться финитными функциями.

Теорема 4.4. Пусть задано марковское семейство t , Px на фазовом пространстве Rn ,Bn такое, что условия (4.11) выпол-

няются при t 0 равномерно по x в пределах каждого ограничен-

ного множества и для каждого ограниченного множества				K Rn
существует ограниченное множество K ' K такое, что
P t, x,K			t	(4.12)
	o
	t 0

равномерно по x Rn \ K ', K ' Rn . Тогда инфинитезимальный оператор данного марковского семейства определен на всех функциях f Cфинит2 и на них он равен L, то есть производящему оператору диффузионного процесса.

Доказательство. Пусть множество K является компактом в пространстве Rn и f x – гладкая финитная функция, обращаю-

щаяся в нуль всюду вне компакта K. Выбираем K ' K, удовлетворяющее условию теоремы. Тогда нужно доказать, что справед-

лив предельный переход t 1 Pf x f x Lf при t 0 равно-

мерно по x Rn. В случае, если x K ', действует теорема 4.1 и, следовательно, теорема 4.4 справедлива; в противном случае, если x Rn \ K ' x K ' , действует условие (4.12) и теорема 4.4 справед-

лива. Таким образом, теорема 4.4 справедлива для всех x Rn. Теорема доказана. ▲

1 В противном случае, для некоторых f Cфинит2 оператор L будет давать неограниченную функцию Lf .

189

Пример 4.5.

Для однородного гауссовского марковского семейства переходная плотность вероятности задается следующей формулой:

1

y m t x 2

p t, x, y

exp

2 2

t

, t 0,

2

t

где параметр m t

удовлетворяет уравнению m t s m t m s ,

а параметр 2 t

связан с функцией m t

следующим условием:

2 t s m2 t 2 s 2 s . Можно доказать, что общее не-

прерывное решение системы приведенных выше уравнений для m t , t имеет вид:

bt					1	e	bt	1 , при b 0,
				ab
m t exp			,	t
	2							при b 0.
				at,

Достаточно легко проверить выполнение условий (4.11) равномерно на каждом компакте по x и условия (4.12). Тогда локальное среднее и локальная дисперсия оказываются равными (соответственно):

b x limt 1 x t	x , t x limt 1 x t x
t 0		t 0
limt 1 m t x x bx 2;
t 0
a x lim t 1 x t	x 2 , t	x limt 1 2 t a.
t 0		t 0

Здесь , t x – ступенчатая функция, отличная от нуля толь-

ко на интервале , . Производящий оператор в данном случае

имеет следующий вид: Lf x af '' x bxf ' x 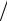2.

Пример 4.6.

Рассмотрим более сложный случай двумерного гауссовского

марковского семейства t ,wt , t	t
	0 wsds, где wt – винеров-
ский процесс.	0

190

Распределение в момент t в начальной точке w0							x, 0 y –
нормальное с математическим ожиданием x, y tx							и матрицей
	t		t2		2
ковариаций	2			3		. Локальные математические ожидания и
		2	t		3
t

локальные ковариации равны производным соответствующих функций в нуле: интеграл по U x, y отличаются от интегралов

по всей плоскости лишь на величину o t ; отсюда можно получить

t 0

b1 x, y 0, b2 x, y x; a11 1, a12 a21 a22 0. Производящий

L

1 2

x

оператор

имеет вид

,

соответственно, действие

2 x2

y

данного оператора на функцию

f x, y

определяется следующим

образом:

Lf x, y

1

2 f

x

f

.

x2

2

y

Важно отметить, что в данном случае производящий оператор оказывается не эллиптическим, а вырождается в параболический; соответствующий процесс, как можно видеть, тоже в каком-то смысле является вырожденным: случайность не проявляется в полной мере – вторая координата полностью определяется первой и фиксацией начальной точки.

Пример 4.7.

Пусть случайный процесс задан в виде сложной случайной функцией t wt , где x – гладкая возрастающая функция

на , ' x 0, x , , причем растущая на бы-

стрее, чем exp Cx2 при любой константе C; wt – винеровский

случайный процесс. В данном случае математическое ожиданиеx t не существует при t 0, но в то же время локальное среднее и локальная дисперсия существуют и равны, соответственно,

b x '' 1 x

2, a x ' 1 x 2

. Производящий опера-

191

	1			1		2	1
тор:	Lf x		'		x	f '' x ''		x f ' x	.	Для рас-
	2

сматриваемого	случая производящий оператор может быть пред-
ставлен в виде	Lf x	1		d 2 f	, u 1 x . Доказательство данного
				du2
	2

соотношения предоставляется читателю.

Пример 4.8.

В данном примере будет определен диффузионный процесс, который (приближенно) описывает процесс изменения численности особей некоторого вида. Пусть коэффициенты рождаемости и смертности1 зависят от общего числа n особей в популяции2 и

равны соответственно r n и l n . На малом отрезке времени можно считать n t n const, следовательно, коэффициенты r,l

тоже можно считать приближенно постоянными. При этом естественное приближение к реальности состоит в том, чтобы считать процессы рождений и смертей на малом интервале времени независимыми пуассоновскими процессами с параметрами nr n и

nl n . Отсюда, справедливы следующие (приближенные) равенст-

ва: n n t n n r n l n t, Dn n t n n r n l n t.

Соответственно, для коэффициентов дифференциального операто-

ра можно получить:						b n n r n l n , a n n r n l n и
дифференциальный					оператор рассматриваемого					диффузионного
процесса			будет записываться				в следующем			виде:	Lf n
	1	n r n l n		d 2 f		n r n l n		df	.
				2
2				dn				dn
	Функцию uN t,n , выражающую вероятность того,										что в мо-
мент t (причем произвольный,							не обязательно малый) число осо-

1То есть средние числа рождающихся и погибающих в единицу времени особей в расчете на одну особь соответственно.

2Простейший аргумент в пользу подобного предположения – от общего числа особей зависит хватит ли всем пищи и, следовательно, увеличение или вырождение данной популяции.

192

бей данного вида будет не больше N , если в начальный момент времени t0 0 число особей было n, можно найти как решение

	uN t,n
задачи Коши:			LuN t,n ,
		t

uN 0,n 1, при n 0и n N.

§4. Результаты Колмогорова.

Прямое и обратное уравнения Колмогорова

Теорема 4.5. Пусть инфинитезимальный оператор диффузионного процесса определен и совпадает с производящим оператором

L на всех непрерывно дифференцируемых функциях	f , убываю-
щих вместе с производными f xi , 2 f xi x j , i,	j 1, ,n на
бесконечности не медленнее, чем некоторая функция x , при-

чем x 0

при

x

. Предположим, что переходные вероят-

ности диффузионного процесса определяются соответствующей переходной плотностью вероятности по формуле

P t, x, p t, x, y dy,

где функция p t, x, y ,	определенная на 0, Rn Rn , непре-

рывна по всем трем своим аргументам вместе с первой частной

производной по t

и частными производными первых двух поряд-

ков по xi , x j . Пусть имеют место следующие оценки:

p

,

p

,

p

,

2 f

C t, y x ,

(4.13)

t

xi

xi x j

где C t, y – непрерывная положительная функция на пространст-

ве 0, Rn . Тогда переходная плотность вероятности удовле-

творяет следующему уравнению:

p t, x, y

1

n

ij

2 p t, x, y

n

i

p t, x, y

a

x

b

x

(4.14)

i

x

j

x

i

t

2 i, j 1

x

i 1

193

или, в более короткой форме1

p t, x, y Lx p t, x, y .

t

Замечание. Условия данной теоремы довольно громоздкие. Например, требуется, чтобы плотность вероятности и ее производные оценивались функцией C t, y x , а не просто C y x . Одна-

ко упрощения здесь недопустимы потому, что соответствующее распределение при t 0 сходится к распределению, целиком сосредоточенному в одной точке, то есть на языке обобщенных

функций x Rn : lim p t, x, y y x , и плотность вероятности

t 0

не может не расти, когда t приближается к нулю. Доказательство. Необходимо отметить, что оценки (4.13) в ус-

ловии теоремы обеспечивают возможность производить дифференцирование под знаком интеграла в следующей формуле:

Pt f x p t, x, y f y dy,

Rn

где f x – произвольная ограниченная измеримая функция, обра-

щающаяся в нуль вне некоторого компакта. Таким образом, можно получить следующие соотношения:

Pt f x

p t, x, y

f y dy,

t

Rn

t

Pt f x

p t, x, y

y dy,

f

(4.15)

x

i

x

i

Rn

2Pt f x

2 p t, x, y

f y dy.

i

x

j

x

i

x

j

x

Rn

При этом, в силу требований, наложенных на рассматриваемую плотность, полученные функции при любом фиксированном t 0 будут убывать на бесконечности не медленнее, чем const x ,

1 Здесь индекс « x » означает, что оператор применяется к плотности веро-

ятности p t, x, y при фиксированных t, y как к функции от x.

194

следовательно, Pt f x будет принадлежать D .		Теперь в качестве
	A
f x возьмем функцию из пространства Cфинит2		; данная функция
также будет принадлежать DA, а для таких функций справедливо
Pt f x t APt	f x . По условию теоремы применение операто-
ра A к функции	Pt f x , убывающей вместе с производными с

указанной в условии теоремы скоростью, равносильно применению производящего оператора L. С учетом данной эквивалентности в применение операторов и используя формулы (4.15), последнее соотношение можно переписать в следующем виде:

p t, x, y

f y dy

Rn

t

1 n

ij

2 p t, x, y

n

i

p t, x, y

a

x

f

y dy b

x

f y dy

i

x

j

x

i

или

2 i, j 1

Rn

x

i 1

Rn

p t, x, y

1 n

ij

2 p t, x, y

n

i

p t, x, y

a

x

b

x

f y dy 0.

t

i

x

j

x

i

R

n

2 i, j 1

x

i 1

Функция в квадратных скобках является непрерывной по y. В силу

того, что интеграл от ее произведения на произвольную гладкую функцию равен нулю, сама рассматриваемая функция тождественно равна нулю. Теорема доказана. ▲

Теорему 4.5 можно перевести на язык дифференциальных уравнений с помощью общего соотношения из теории полугрупп

dPt f AP ' f ; dt

приведенная ниже теорема выводится из соотношения

dPt f Pt Af . dt

Введем некоторые дополнительные ограничения на коэффициент-

ные функции aij x

и bi x в дифференциальном операторе:

195

пусть функция aij x дважды, а bi x один раз непрерывно диф-

ференцируемы (ограниченность производных не предполагается). Тогда для дифференциального оператора определен (на гладких

функциях) формально сопряженный оператор L* :

*	1	n	2
L g x
			i	x	j
	2 i, j 1		x

Теорема 4.6. Пусть t

	ij			n			i
a		x g x			x	i b		x g x	.
				i 1
,Px		– диффузионный процесс с произ-

водящим оператором L. Предположим, что плотность вероятности перехода обладает непрерывными частными производными перво-

го порядка по t и первых двух порядков по

yi , y j . Тогда переход-

ная плотность удовлетворяет следующему уравнению:

p t, x, y

1 n

2 aij y p t, x, y

n bi y p t, x, y

(4.16)

i

y

j

y

i

t

2 i, j 1

y

i 1

или, в более короткой форме1

p t, x, y

L*y p t, x, y .

t

Доказательство. Пусть взята произвольная функция f Cфинит(2) .

Тогда f DA и справедлива следующая цепочка соотношений:

Pt f x Pt Af x Pt Lf x .

t

Записывая данные равенства через плотность вероятности и ее частную производную по t, можно получить следующую формулу:

p t, x, y

f y dy

t

Rn

1

n

2

f

y

n

f y

p t, x, y

aij y

bi y

dy.

i

j

i

R

n

2 i, j 1

y y

i 1

y

1 Здесь индекс « y » означает, что оператор применяется к плотности ве-

роятности p t, x, y при фиксированных t, x как к функции от y.

196

Разобьем интеграл, стоящий в правой части, на n2 интегралов со вторыми частными производными и на n интегралов с первыми производными. Далее, в каждом из полученных интегралов выпол-

ним интегрирование по частям. Для финитной функции

f y

вне-

интегральные члены будут исключены,

в результате

можно полу-

чить следующее равенство:

p t, x, y

1

n

2

aij y p t, x, y

n

bi y p t, x, y

2

i

y

j

y

i

R

n

t

i, j 1

y

i 1

f y dy 0.

Аналогично рассмотренному выше доказательству теоремы 4.5, в данном случае функция в квадратных скобках является непрерывной по y. В силу того, что интеграл от ее произведения на произвольную гладкую функцию равен нулю, сама рассматриваемая функция тождественно равна нулю. Теорема доказана. ▲

Пример 4.9.

Для процесса диффузии справедливо следующее равенство для плотности вероятности:

p		1		2 p			p
			a			b		bp .
		2		y	2		y
t

Полагая p t 0, из (4.16) получается уравнение плотности меры инвариантной относительно меры Лебега: L*y p 0.

Уравнение (4.14) называется обратным уравнением Колмогорова, уравнение (4.16) – прямым уравнением Колмогорова или уравнением Фоккера – Планка.

Поясним более подробно, с чем именно связаны названия «обратное» и «прямое» уравнение.

Для неоднородного по времени процесса t , Ps,x можно дока-

зать соответствующие аналоги теорем 4.5 и 4.6, в которых будут участвовать локальные ковариации aij s, x и локальные средние

197