
Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009
.pdf6. Если Cn – последовательность таких положительных чисел,
|
|
f |
n |
x |
|
|
n |
то начиная с некоторого значения ин- |
|||||||
что x 0,1 : |
|
|
C , |
||||||||||||
декса n справедливо следующее неравенство: |
|
|
|
|
|||||||||||
|
|
|
|
4 |
n |
n |
|
4r |
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
n |
, |
0 1. |
|
|
|
|||
|
|
|
|
D |
|
D |
|
|
|
||||||
|
|
|
|
|
n |
1 |
|
n |
|
|
|
|
|
|
|
7. Знак разности |
|
fn x hn fn x , |
начиная с некоторого номе- |
||||||||||||
0 |
|
|
|
|
|
|
|
|
n |
|
|
|
и для всех |
|
0 |
ра n не зависит от значения h для всех x 0,1 |
n n . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда функция |
|
f x , |
являющаяся суммой ряда fn x |
из |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
условия 2, ни в одной точке x 0,1 не будет иметь конечной про-
изводной. Бесконечную производную данная функция может иметь на бесконечном множестве точек [60, 61].
Позже У. Дини показал [61], что при некоторых дополнительных предположениях такая функция f x ни в одной точке не бу-
дет иметь и бесконечной производной. Важно отметить, что класс функций, удовлетворяющих теореме Дини, бесконечен [60], в частности, в нем содержится функция Вейерштрасса W x [61].
В 1879 г. Дарбу предложил достаточно общий метод построения недифференцируемых функций [62]. Он изучал функции x ,
определяемые следующим рядом:
|
f anbn x |
|
|
|
x |
, |
(2.4) |
||
|
||||
n 1 |
an |
|
||
где an и bn – некоторые последовательности действительных чисел, f x – непрерывная ограниченная функция с ограниченной второй производной. Если последовательности an и bn выбра-
ны так, что при фиксированном k |
справедливы соотношения |
|||||
lim |
an |
0, |
lim |
a1b12 |
a2b22 an kbn2 k |
0, |
|
|
an |
||||
n an 1 |
n |
|
||||
78

то ряд (2.4) сходится к некоторой непрерывной функции x .
При некоторых дальнейших ограничениях на выбор an , bn ,k и f x можно получить непрерывные функции, не имеющие произ-
водной ни в одной точке. Так, если n : bn 1 и k 1, то на члены последовательности an достаточно наложить условие
lim a1 a2 an 1 0,
n an
которому удовлетворяют, например, числа n!, чтобы можно было указать бесконечное множество функций f x , для которых соот-
ветствующая функция (2.4) не дифференцируема ни в одной точке. В частности, при всех f x cos x функция x нигде не диффе-
ренцируема. При выборе bn n 1,k 3 и f x sin x из общего соотношения (2.4) получается недифференцируемая функция x
из работы Дарбу [59].
В 1918 г. метод построения непрерывных недифференцируемых функций был предложен К. Кноппом [63]. Можно даже сказать, что после упомянутых выше работ была создана целая индустрия по производству как отдельных недифференцируемых функций, так и целых их классов.
Замечание. Пример функции Вейерштрасса опирается на свойства лакунарного ряда, то есть такого ряда, в котором члены, отличные от нуля «очень редки и разбросаны» [64, 65].
Понятие лакунарного тригонометрического ряда было введено Ж. Адамаром в 1892 г. при изучении функций, не продолжаемых аналитически за границу сходимости [66].
Определение 2.1. Лакунарным (в смысле Адамара) тригонометрическим рядом называется ряд следующего вида:
|
|
a0 |
|
|
|
cos n |
|
x b sin n |
|
x |
|
|
|
|
a |
k |
k |
k |
(2.5) |
||||
|
|
|
|||||||||
|
2 |
|
|
|
k |
|
|
||||
|
|
k 1 |
|
|
|
|
|
|
|
||
при nk 1 |
nk q 1. |
|
|
|
|
|
|
|
|
||
Таким образом, номера nk лакунарного ряда (2.5) при всех k растут не медленнее геометрической прогрессии со знаменателем,
79

большим единицы. В [48] было также доказано, что функция Вейерштрасса W x не имеет конечной производной ни в одной точке
при выполнении следующих условий: a 1,b 1 и ab 1.
§3. Множества первой и второй категории по Бэру
Чтобы корректно рассмотреть вопрос о месте, занимаемом дифференцируемыми функциями в множестве всех непрерывных функций, представляется важным напомнить некоторые понятия, относящиеся к множествам (подробнее – см., например, [39]). Для данного случая вводится удобное определение согласно [67 – 69].
Определение 2.2. Множество M называется топологическим пространством, если всякому подмножеству X M поставлено в
соответствие подмножество X M так, что выполнены следующие аксиомы:
1)X Y X Y ;
2)X X ;
3), – пустое множество;
4)X X .
Определение 2.3. Множество X называется всюду плотным в топологическом пространстве M , если X M.
Определение 2.4. Множество X называется граничным, если его дополнение в топологическом пространстве M является всюду
плотным множеством, то есть M \ X M .
В 1899 г. Бэр сформулировал следующее определение. Определение 2.5. Множество X топологического пространства
M называется множеством первой категории на M , если оно является объединением счетного семейства множеств нигде не плотных на M .
Определение 2.6. Множества второй категории определяются как множества, не являющиеся множествами первой категории.
Согласно теореме Бэра справедливы следующие утверждения: - дополнение любого множества первой категории на прямой
является плотным;
80
-никакой интервал на множестве действительных чисел R не является множеством первой категории;
-каждое счетное множество на прямой является множеством первой категории и множеством меры нуль;
-в множестве действительных чисел рациональные числа образуют множество первой категории.
Простейшим примером несчетного множества, принадлежащего
кмножеству первой категории и к множеству меры нуль, является канторово совершенное множество, имеющее мощность континуума. Доказывается, что прямую можно разбить на два взаимно дополняющих друг друга множества A и B так, что множество A будет являться множеством первой категории, а множество B – иметь меру нуль.
Во многих проблемах топологии и теории функций множества первой категории играют роль, аналогичную роли множеств меры нуль в теории меры (то есть множеств, которыми можно пренебречь).
При доказательстве теорем существования в теории множеств часто пользуются так называемым методом категорий, который основан на теореме Бэра, согласно которой всякое метрическое пространство является множеством второй категории на самом себе [57]. На основе данного утверждения доказывается следующая важная теорема.
Теорема 2.2. Пусть C 0,1 – пространство непрерывных функций
x t , наделенное нормой |
x |
|
|
|
max |
|
x t |
|
. Пусть G – множество |
|
|
|
|
|
t 0,1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
функций из C 0,1 , которые не имеют конечной правой производной ни в одной точке t 0,1 . Тогда G является множеством второй
категории по Бэру на пространстве C 0,1 , а его дополнение являет-
ся множеством первой категории по Бэру [70, 71].
Из приведенных выше определений и теорем следует исключительно важный вывод: множество функций, имеющих конечную одностороннюю производную хотя бы в одной точке t 0,1 , явля-
ется пренебрежимо малым в смысле категории Бэра по сравнению с множеством всех непрерывных функций. Тем более данное ут-
81
верждение справедливо для функций с конечной обычной производной. Доказательство данного утверждения и приведенной выше теоремы приведено в [69], а в [72] показано, что множество таких функций образует коаналитическое неборелевское подмножество пространства 0,1 .
Как отмечено в работе [41], классы непрерывных функций без производных, рассмотренные в XIX веке и в первые два десятилетия XX века, не давали примера такой сингулярной непрерывной функции, у которой ни в одной точке не существовала бы конечная или бесконечная (левая или правая) производная. Например, у функции Вейерштрасса W x (2.2) имеется односторонняя произ-
водная на всюду плотном множестве.
Первый пример такой в сильном смысле недифференцируемой функции был построен в 1922 г. и опубликован в 1924 г. А.С. Безиковичем [73]. В связи с этим Банах и Штейнгауз поставили следующий важный вопрос о распространении с помощью метода категорий результата С. Мазуркевича и Банаха на функции типа функции Безиковича: можно ли показать, что дополнение множества всех непрерывных функций, не имеющих ни в одной точке ни конечной, ни бесконечной производной, является множеством первой категории?
В 1932 г. С. Сакс дал отрицательный ответ на данный вопрос. Он показал [74], что множество непрерывных на отрезке 0,1
функций, у которых или существует конечная правая производная, или эта производная равна на множестве мощности континуум, есть множество второй категории в пространстве всех непрерывных функций.
Таким образом, можно сделать исключительно важный вывод: класс функций, односторонне дифференцируемых хотя бы в одной точке, в смысле категорий существенно шире класса функций, имеющих обычную производную хотя бы в одной точке.
Соответственно, класс функций, не имеющих ни конечной, ни бесконечной односторонней производной в каждой точке отрезка, уже в смысле категорий класса функций, нигде не имеющих двухсторонней производной.
82
По словам С. Сакса «… это быть может объясняет трудности с нахождением первого примера функции, не имеющей конечной или бесконечной односторонней производной в каждой точке …»
[74].
Таким образом, непрерывные дифференцируемые функции, в основном используемые в физических исследованиях, составляют существенно малую часть (подмножество меры нуль) множества всех непрерывных функций. Естественно, что попытки корректно и на количественном уровне описывать, в частности, сложные многочастичные процессы, фазовые переходы, резко нерегулярные и квазихаотические явления в физике микромира и квантовой теории поля привели к необходимости введения аппарата недифференцируемых (фрактальных) функций, который является относительно новым для физиков и в то же время достаточно давно известен математикам. Важно отметить, что раздел недифференцируемых функций имеет прочную и строгую фундаментальную математическую основу.
С целью расширения известных классов недифференцируемых функций В. Орлич в 1947 г. нашел достаточно общие условия, при которых непрерывные функции, являющиеся суммами равномерно сходящихся рядов, нигде не дифференцируемы [75]. Однако общность результатов была достигнута за счет того, что коэффициенты этих рядов задавались неэффективно, с использованием метода категорий. Такой подход сам В. Орлич охарактеризовал как «в некотором смысле промежуточный» между «эффективными» способами задания недифференцируемых функций в виде рядов и «неэффективным» методом Мазуркевича – Банаха [75].
Таким образом, класс непрерывных функций, не имеющих производной ни в одной точке, неизмеримо богаче класса функций с производными.
Как метко было отмечено в [41] «… создалась любопытная ситуация, когда оказалось, что те непрерывные функции, которые изучались математиками на протяжении веков, те функции, которые использовались для описания (физических) явлений внешнего мира, – эти функции оказались принадлежащими лишь пренебрежимо малому классу всех непрерывных функций …». Постепенно с течением времени математики привыкли к тому, что нигде не дифференцируемые функции действительно существуют, но физики
83

долго не соглашались с этим и воспринимали такие функции в виде неких «монстров», «уродливых порождений математических фан-
тазий», не имеющих отношения к миру реальных физических явлений1.
Важно отметить, что с позиций современной физической науки функция без производной вовсе не абстрактное понятие, такая функция описывает реальное физическое явление, в частности, траекторию движения броуновской частицы. В настоящее время идеи фрактальной геометрии и соответствующие ей разделы математического анализа, в частности, связанные с недифференцируемыми функциями, интегродифференциальным исчислением дробных порядков (см. ниже), все более широко используются в современных физических исследованиях.
Великий ученый Н. Винер писал: «… В рамках этой теории мне удалось подтвердить замечание Перрена, показав, что за исключением множества случаев, имеющих суммарную вероятность нуль, все траектории броуновского движения являются непрерывными нигде не дифференцируемыми кривыми …» [77].
Существенным моментом является то, что в спектральной теории стационарных случайных процессов недифференцируемые функции возникают совершенно естественно и избежать их возможно лишь при отказе от имеющего ясный физический смысл условия стационарности, единственно делающего данную теорию простой и наглядной [76].
Ввиду важности кратко поясним данное утверждение.
При спектральном разложении стационарного процесса X t
использование интеграла Стилтьеса оказывается неизбежным в силу того, что случайная функция Z не является дифференци-
руемой ни в каком смысле, и поэтому никак нельзя перейти от интеграла Фурье – Стилтьеса
X t ei tdZ
1 Долгое время физики исходили из принципа «в физике все функции дифференцируемы» [76].
84

к обычному интегралу Фурье. В случае существования спектральной плотности f всегда справедливо следующее соотношение:
|
dZ |
|
2 |
f d . |
(2.6) |
|
|
В силу соотношения (2.6) во всех реальных физических случаях, когда процессу X t соответствует положительная спектральная
плотность |
f , средний квадрат приращения Z случайной |
функции |
Z на малом отрезке оси частот будет близок к |
величине |
f , то есть имеет тот же порядок малости, что и |
величина . В таком случае само значение приращения Z |
|
имеет, как правило, порядок 
 , что несовместимо с допущени-
, что несовместимо с допущени-
ем о дифференцируемости случайной функции Z , то есть о существовании предела отношения Z 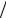 при 0 [78].
при 0 [78].
Как отмечено в работе [76] «… мы сталкиваемся здесь с довольно редким случаем, когда в задаче, имеющей реальный физический смысл, возникают нигде не дифференцируемые функции, которые еще совсем недавно многим прикладникам представлялись заумной математической абстракцией, которая не может иметь никаких приложений …».
В арсенале математика нашелся и аналитический аппарат для адекватного и строгого описания таких объектов и процессов. Место обычной размерности заняла размерность Хаусдорфа (подробнее – см. [39]), а место обычной производной – дробная производная или показатель Гельдера.
§4. Интегралы и производные дробного порядка: краткая историческая справка
Представляется важным отметить, что мысль об обобщении по-
нятия дифференцирования |
d p f x dx p на нецелые значения по- |
рядка дифференцирования |
p возникла практически с самого воз- |
никновения дифференциального исчисления.
85
Первая попытка обсуждения идеи обобщения понятия производной на любые порядки, зафиксированная историей, содержится в переписке создателя дифференциального исчисления Г. Лейбница. В своих письмах к Г. Лопиталю (1695 г.) и Уоллису (1697 г.) Г. Лейбниц сделал несколько замечаний о возможности рассматривать дифференциалы и производные дробного порядка, а именно, для p 1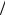 2.
2.
Следующий шаг, который можно рассматривать как первую попытку количественного решения проблемы производных произвольного порядка, был сделан Л. Эйлером (1738 г.), заметившим, что результатам вычисления производной d p x 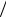 dx p от степенной функции можно придать смысл при нецелых значениях порядка дифференцирования p. П. Лаплас (1812 г.) высказал идею о возможности (нецелого) дифференцирования функций, которые можно представить с помощью следующего интеграла:
dx p от степенной функции можно придать смысл при нецелых значениях порядка дифференцирования p. П. Лаплас (1812 г.) высказал идею о возможности (нецелого) дифференцирования функций, которые можно представить с помощью следующего интеграла:
F t t xdt,
где F t – некоторая функция.
В трактате С. Лакруа (1820 г.) повторена мысль Л. Эйлера и уже приведена явная формула вычисления производной дробного порядка d1 2 x
2 x 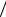 dx1
dx1 2 от степенной функции.
2 от степенной функции.
Следующий шаг в развитии данного направления аппарата интегродифференциального исчисления сделал Ж. Фурье (1822 г.), который предложил использовать равенство
d p f x |
|
1 |
|
p |
|
|
|
||
|
|
|
|
|
|
d |
f t cos tx t p |
|
dt |
dx |
p |
2 |
|
2 |
|||||
|
|
|
|
|
|
|
|||
для определения производной нецелого порядка. Важно отметить, что это было первое определение производной любого положительного порядка от любой (достаточно «хорошей») функции, и, что примечательно, дано это определение было еще в первой половине XIX века.
Таким образом, дифференцирование и интегрирование дробных порядков имеет достаточно длительную историю развития и является неотъемлемой частью математического анализа. В настоящее время в связи с развитием теоретических и экспериментальных методов физических исследований данный раздел математики нахо-
86

дит все более широкое применение при решении различных задач, в том числе и в физике фундаментальных взаимодействий.
Описанные выше эпизоды можно отнести к предыстории развития аппарата дробного интегродифференциального исчисления1. Собственно историю интегрирования и дифференцирования дробных порядков следует вести с работ Н. Абеля и Ж. Лиувилля. В работах Н. Абеля 1823 г. и 1826 г. в связи с так называемой задачей о таутохроне было решено следующее интегральное уравнение:
t
dt f x , x a,0 1. (2.7)
a x t
Вобеих указанных выше работах Н. Абеля решение было дано дляx
произвольного значения 0,1 , хотя задача о таутохроне приво-
дит к случаю 1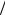 2. Хотя работы Н. Абеля и не были выполнены в русле идей обобщения дифференцирования на произвольные порядки, они сыграли важную и непосредственную роль в их развитии. Это связано с тем, что левая часть уравнения Н. Абеля (2.7) представляет собой, как выяснится позже, операцию дробного интегрирования порядка 1 , а обращение данного уравнения – операцию дробного дифференцирования соответственно. Однако в такой форме понятия дробного интегродифференциального исчисления были сформулированы позже.
2. Хотя работы Н. Абеля и не были выполнены в русле идей обобщения дифференцирования на произвольные порядки, они сыграли важную и непосредственную роль в их развитии. Это связано с тем, что левая часть уравнения Н. Абеля (2.7) представляет собой, как выяснится позже, операцию дробного интегрирования порядка 1 , а обращение данного уравнения – операцию дробного дифференцирования соответственно. Однако в такой форме понятия дробного интегродифференциального исчисления были сформулированы позже.
В 1832 – 1837 г.г. появляется серия работ Ж. Лиувилля, сделавших его по праву создателем уже достаточно полноценной картины интегродифференциального исчисления дробных порядков. Хотя теория, созданная Ж. Лиувиллем, еще и не достигла той формы, которую ей придало дальнейшее развитие подходов дробного интегрирования и дифференцирования другими исследователями, но в ней уже были высказаны и далеко продвинуты важные идеи. Ис-
1 Здесь и далее, если специально не оговорено, под термином «дробное интегродифференциальное исчисление» понимается, естественно, интегродифференциальное исчисление дробного порядка, то есть именно дробный порядок интегрирования / дифференцирования. Ниже в соответствии с установившимися понятиями и для краткости будут использоваться сочетания «дробное интегродифференциальное исчисление, дробное интегрирование / дифференцирование».
87
