Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

2)класс E2 конечных пересечений подмножества из E1;

3)класс E3 конечных объединений попарно непересекающихся подмножеств из E2.

Построенный таким образом класс E3 совпадает с булевой алгеброй, порожденной классом E.

Важно отметить, что предложение 3.2 дает конкретную конструкцию булевой алгебры, порожденной классом E.

§3. Пространства, классы и алгебры в теории вероятности

Определение 3.11. Вероятность P на булевой алгебре A подмножеств множества есть отображение булевой алгебры A в множество действительных чисел, удовлетворяющее следующим аксиомам:

1)A A : 0 P A 1, P 1;

2)для любого конечного семейства Ai ,i I попарно непересе-

кающихся событий справедливо P	Ai P Ai – свойство
	i	i

аддитивности;

3) для любой последовательности событий An ,n 1 монотонно

стремящейся к , такой, что	A1 A2 An и	An ,
		n

справедливо lim P An 0	– свойство непрерывности в относи-
n

тельно монотонных последовательностей.

Ниже приведены свойства вероятности, являющиеся простыми следствиями аксиом 1) и 2)1:

а) P 0;

б) если A1, A2 A и A1 A2, то P A1 P A2 – свойство монотонности;

1 Ими обладают, естественно, также те функции множеств, которые не удовлетворяют аксиоме 3) в определении 3.11.

118

в) A1, A2 A : P A1 P A2 P A1 A2 P A1 A2 – свойст-

во сильной аддитивности;

г) конечного семейства событий Ai ,i I справедливо соот-

ношение: P	Ai P Ai – свойство полуаддитивности.
	i	i

Определение 3.12. Булевой -алгеброй (или борелевским полем) подмножеств множества называется класс A подмножеств множества , содержащий , и замкнутый относительно операций дополнения, счетного объединения и счетного пересечения.

Определение 3.13. Пара ,A , состоящая из множества и

(булевой) -алгебры A подмножеств множества , называется измеримым пространством.

Необходимо отметить, что для того чтобы класс A подмножеств множества был -алгеброй, достаточно, чтобы он содержал , и был замкнутый относительно операций дополнения и счетного объединения.

Определение 3.14. Измеримое пространство ,A называется

фазовым пространством, если -алгебра A содержит все подмножества , состоящие из одной точки.

Определение 3.15. Пусть E1 и E2 являются непустыми множе-

ствами и определено преобразование : E1 E2. Пусть F – неко-

торая система подмножеств множества E2. Полным прообразом1 F называется множество 1 , F 1 F .

Замечание. Определение 3.15 применимо и в том случае, когда отображение определено лишь на некотором подмножестве E множества E.

Пусть даны измеримые пространства E1,A1 , , En ,An . Мож-

но образовать топологическое произведение, определяемое следующим образом: E1 E2 En x1, , xn ; i 1, n : xi Ei . Будем обозначать -алгебру в построенном выше топологическом произведении E1 E2 En , которая порождается множествами

119

вида 1 2 n i Ai , i 1, ,n , через A1 A2 An. В ча-

стном случае, если E = E	2	E	n	E, будем писать En	вместо
1
E1 E2 En. В случае,		когда A1 = A2 An A, будем пи-
сать An вместо A A A соответственно.
1 2		n

Предположим далее, что задана бесконечная последовательность измеримых пространств En ,An , n 1,2, Условимся обо-

значать через E1 E2			En множество всех последователь-
ностей	x1, , xn , ,		где n 1,2, : xn En и обозначать через
A1 A2	An -алгебру в этом множестве, порожденную
подмножествами		вида A1 An En 1 En 2 , n 1,2, , где
i 1, n : Ai Ai .		В частном случае одинаковых сомножителей

указанные выше объекты будут обозначаться E и A соответственно.

Определение 3.16. Отображение : E1,A1 E2,A2 измери-

мого пространства E1,A1 в измеримое пространство E2 ,A2 на-

зывается измеримым отображением, если 1 A2 A1.

Определение 3.17. Для всякой монотонно возрастающей последовательности An ,n 1 A1 A2 An подмножеств мно-

жества положим

lim An An.

n

n

Определение 3.18. Для всякой монотонно убывающей последо-

вательности An ,n 1 A1 A2	An подмножеств множе-
ства положим
lim A		A .
n	n	n
		n

Определение 3.19. Класс E подмножеств множества называется монотонным, если он замкнут относительно операций lim

и lim 1.

1 Здесь имеются в виду пределы по последовательностям.

120

Предложение 3.3. Для того, чтобы булева алгебра A была - алгеброй, необходимо и достаточно, чтобы она была монотонным классом1.

Определение 3.20. Множество N в вероятностном пространст-

ве ,A,P называется нулевым (относительно вероятности P ),

если существует множество A A, такое, что N A, P A 0.

Определение 3.21. Вероятностное пространство ,A,P назы-

вается полным, если A содержит все P -нулевые подмножества множества .

Для дальнейшего рассмотрения представляется важным напомнить понятие булевой полуалгебры, являющееся вспомогательным понятием, которое оказывается особенно полезным при изучении вероятностей на действительной прямой и в произведении пространств.

Определение 3.22. Класс J подмножеств множества называется булевой полуалгеброй, если он удовлетворяет следующим условиям:

1), J;

2)класс J замкнут относительно конечных пересечений;

3)дополнение Sc каждого множества S J есть объединение

конечного семейства попарно непересекающихся подмножеств множества из класса J.

Теорема 3.1. Булева алгебра A,	порожденная булевой полуал-
геброй J подмножеств множества	, состоит из сумм	A Si
		i

конечных семейств Si ,i I попарно непересекающихся подмно-

жеств множества , принадлежащих классу J.

Для каждой аддитивной функции множеств P, отображающей класс J в отрезок 0,1 , и такой, что P 1, равенство

P' A P Si

i

1 Доказательство данного предложения предоставляется читателю.

121

(корректно) определяет единственное аддитивное продолжение P' функции P на алгебру A. Если функция P является - аддитив-

ной на классе J, то функция P' является вероятностью на алгебру A; в этом случае существует единственная продолжающая вероятность P на -алгебре, порожденной на классе J (совпадающая с-алгеброй, порожденной A ).

Доказательство. Класс S сумм Si							есть булева алгебра под-
					i
множеств множества . Действительно,							данный класс содержит в
качестве элементов и ;			является замкнутым относительно ко-
		i			j			i	j
нечных пересечений:
		S			S'			S	S' ; является замкну-
i I				j J			I J

тым относительно образования дополнений, то есть справедливо:

			c
			Sic	и Sic S в силу аксиомы (3) определения булевой
	Si
i I			i I

полуалгебры (определение 3.22). Очевидно, что класс J порождает

S.

Для доказательства корректности определения P' на S необходимо показать, что если Si S'j , то P Si P S'j .

			i I	j J		i I	j J
	Используя	Si Si S'j , S'j			Si	S'j ,	а также свойство
			j J		i I
аддитивности рассматриваемой функции множеств P								и булевой
полуалгеброй		J,	можно	получить		следующие		равенства:
P Si P Si			S'j P S'j .		Таким образом, корректность
i I	I J		j J

доказана.

Докажем ниже аддитивность (а именно, -аддитивность) про-

должения функции множеств P P' на классе S. Если конечное

(счетное) семейство множеств A j Sij из класса	S ( Sij J,
i I j
множество I j конечно), пронумерованных индексами	j J, есть

122

разбиение некоторого множества A Sk из S, то используя

k K

разложения Sk Sij Sk , k K; Sij Sij Sk , i I j , j J

j J i I j k K

и свойство аддитивности ( -аддитивности) функции множеств P на классе S, можно последовательно получить следующие равен-

ства: P' A P Sk P Sij Sk P Sij Sk

k K

k K j J i I j

j J i I j k K

P Sij P' Aj . Таким образом, аддитивность доказана.

j J i I j

j J

Единственность продолжения функции P' очевидна. Последнее утверждение данной теоремы есть следствие из теоремы о продолжении. Теорема доказана. ▲

В теории вероятности нередко бывает трудно, а иногда и вообще невозможно доказать, что построенная некоторым образом функция множеств обладает свойством -аддитивности, даже если эта функция аддитивна по построению. Тем не менее в довольно широком классе случаев можно установить -аддитивность аддитивной функции множеств, доказав, что рассматриваемое пространство удовлетворяет некоторому дополнительному условию компактности. Введем данное условие в наипростейшей возможной форме.

Определение 3.23. Класс E подмножеств множества назы-

вается компактным, если для любой последовательности Cn n 1

множеств из класса E, для которых Cn , существует целое

n 1

число N , такое, что Cn .

n N

§4. Меры и интегралы

Определение 3.24. Пусть E,A – измеримое пространство. Не-

отрицательная функция

123

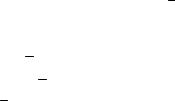
	: A R ,
где A – -алгебра на E,	R 0, , называется мерой, если для

любого конечного или счетного набора 1, 2 , , n , попарно непересекающихся множеств из A справедливо равенство

i i .

i i

Определение 3.25. Пусть – мера в измеримом пространстве

E,A . Если E , то и A : . В этом случае рас-

сматриваемая мера называется конечной.

Подкласс класса конечных мер образуют так называемые веро-

ятностные меры, для которых E 1.

Определение 3.26. Мера называется -конечной, если най-

дется последовательность множеств n n 1 , n,n 1,2, : n A

такая, что n E и n,n 1,2, : n .

			n
Пусть – мера в измеримом пространстве E,A . Положим
			если найдутся множества 1, 2 из A такие, что справедли-
A		,
во 1
			2 и 1 2 . Система A				является -алгеброй
в пространстве E,A .
					называется пополнением по ме-
Определение 3.27. Система A
ре .

Если положить 1 2 , коль скоро справедливы соотношения: 1 2 , 1, 2 A и 1 2 , то можно получить некоторую меру на -алгебре A, являющуюся продолжением первоначальной меры, заданной на -алгебре A.

Определение 3.28. Продолженная указанным выше образом мера на -алгебру A называется пополнением меры .

Из включения A A следует, что всякая A -измеримая функция является также A -измеримой.

124

Предположим теперь, что в измеримом пространстве E,A за-

дана совокупность мер M . Пересечение всех -алгебр, по-

лучающихся пополнением A по мерам M, также является - алгеброй.

Определение 3.29. Полученная указанным выше способом - алгебра называется пополнением -алгебры A по системе мер

M .

На эту -алгебру естественно продолжаются все меры M.

Необходимо заметить, что если A является пополнением A по

некоторой системе мер M, то пополнение A по системе мер M

совпадает с A.

Лемма 3.2 (Бореля – Кантелли). Пусть E,A – измеримое

пространство, – мера на данном измеримом пространстве

E,A , и задана An n 1 – последовательность элементов An A

такая, что числовой ряд An сходится. Тогда мера множества

n 1

точек x, принадлежащих одновременно бесконечному числу эле-

ментов последовательности An n 1 , равна нулю.

К данной лемме мы вернемся позже, переформулировав ее на языке вероятностей и обсудив ее значение для эксперимента1.

Определение 3.30. Пусть – мера на измеримом пространстве

E,A , пусть также заданы некоторая функция f x и последова-

тельность функций fn x n 1 , являющихся A -измеримыми функ-

циями. Если 0 : lim	x;	fn x f x		0, то говорят,
n
что последовательность функций fn x			n 1	сходится к функции
f x по мере и пишут	fn x
		f x .
		n

1 Данное обсуждение будет выполнено в §5, переформулированная на языке вероятности лемма будет обозначена как лемма 3.6 соответственно.

125

Лемма 3.3. Пусть E,A – измеримое пространство, каждой паре натуральных чисел m n поставлена в соответствие неотри-

цательная A -измеримая функция fnm x , x E, и пусть при некотором l m n : fnl x fml x fnm x и для каждого 0 вы-

полнено lim x; fnm x 0. Тогда из любой стремящейся к

m,n

последовательности чисел можно выбрать подпоследователь-

ность m

k 1

такую, что lim

f mk x 0

для почти всех (отно-

k

k,l

nl

сительно )

x E, то есть для всех x E, не входящих в некоторое

множество A, для которого 0.

Данная лемма приводится без доказательства, которое можно

найти в [115, 116].

На основе сформулированной леммы можно доказать следую-

щие предложения.

Предложение 3.4. Пусть E,A

– измеримое пространство, если

для последовательности функций

fn x

присутствует сходи-

n 1

: fn

мость по мере

x f x ,

то найдется подпоследователь-

n

ность

fnk x

такая, что имеет место сходимость

fn x

k 1

n 1

fn

x

f x для почти всех (относительно )

x E.

k

k

Предложение 3.5. Пусть – мера на измеримом пространстве

E,A , если 0 :

lim x;

fn x fm x

0, то последо-

m,n

сходится по мере

к некоторой

вательность функций fn x

n 1

f x ,

то есть fn x

функции

f x .

n

Предложение 3.6. Пусть – мера на измеримом пространстве

E,A , если данная мера конечна и последовательность функций

сходится к некоторой функции

f x ,

fn x f x ,

fn x

n 1

n

126

для почти всех (относительно )		x E, то имеет место и сходи-
мость по данной мере: fn x
	f x .
	n

Определение 3.31. Пусть – мера на измеримом пространстве

E,A . Пусть f x – A -измеримая функция, определенная на не-

котором подмножестве E f E и пусть A E f . Говорят, что функ-

ция f x является -суммируемой функцией на A, если сущест-

вуют следующие конечные пределы:

k

k

f x

k 1

lim

x : x A,

,

k 0 n

n

n

n

k 1

k

k 1

lim

x : x A,

f x

.

n

n

n k 1

n

Сумма данных пределов называется интегралом функции f x по мере и обозначается следующим образом:

f x dx .

A

Если один из указанных пределов бесконечен, а другой имеет конечное значение, то интегралу приписывают значение (если бесконечен первый предел) или (если бесконечен второй предел).

Замечание. В тех случаях, когда говорится о -суммируемой функции без указания какого-нибудь конкретного множества A, имеется в виду функция, -суммируемая на всей области определения.

Перечислим некоторые важные свойства определенного выше интеграла1.

1. Лемма Фату.

1 Во избежание излишнего загромождения изложения, данные свойства приводятся без доказательств, которые являются несущественными для дальнейшего рассмотрения.

127