Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

на границу области допускает конечную верхнюю грань, не зависящую от начального положения точки.

Доказательство. Пусть – ограниченная область в R2 . Тогда

a diam sup p, p'						– некоторое действительное число,
		p, p '
где diam – диаметр рассматриваемой области,								p, p' – рас-
стояние между двумя элементами области .							Вероятность того,
что точка	A 1			является внутренней точкой области					, меньше,
чем величина k P A 0 A 1 a 1 exp a2							2 1		(ибо a 0 ),
где A 0 A t				– точка, соответствующая положению подвиж-
				t 0	A в начальный момент времени t 0 и
ной броуновской точке
A 1 A t		– точка,			соответствующая положению подвижной
		t 1							n 1,2,
броуновской точке A в момент времени t 1.							Тогда
P T n P A 0 A 1 a, , A n 1 A n a kn ,								следовательно,
математическое				ожидание		T kn ,	ибо	возрастающая
						n 0

(вследствие условия 0 k 1) ограниченная сверху последователь-

	n
ность частичных сумм			сходится в своей верхней грани.
	k s
	s 0	n 1
Лемма доказана. ▲
Замечание. Можно доказать, что
P T t cn exp nt ,				(5.11)
		n 1

где cn – положительные постоянные, n – характеристические числа, при которых уравнение диффузии в частных производных имеет решения, не равные тождественно нулю и обращающиеся в нуль на .

Теорема 5.7. Замыкание плоской броуновской кривой C, продолженной неограниченно, почти наверное совпадает со всей плоскостью R2 .

228

Другими словами: пусть D – произвольная открытая квадрируемая область в R2 , площадь которой отлична от нуля. Вероятность того, что C содержит точки области D равна единице.

Доказательство. Теорему достаточно доказать для открытого круга BR 0 радиуса R с центром в начале координат O 0,0 .

Пусть положение подвижной броуновской точки A t в некото-

рый момент t 0 A 0 A t		t 0	известно и r A 0 ,O . Ве-
роятность того, что C содержит внутренние точки круга BR 0
выражается некоторой функцией			r и она равна единице

при r R, убывая с ростом r. Поэтому предположим, что r R. Рассмотрим в качестве области круг радиуса r с центром в точ-

ке O и различные интервалы tn' ,tn'' ,n 1,2, такие, что:

1)	точки A tn'			и A tn'' лежат на – границе области	,
представляющей собой окружность;
2)	t tn' ,tn''			броуновская точка A t \ , то есть для ука-
занных моментов времени A t пребывает внутри области ;
3)		'	''
	t tn		,tn :	A t BR O или A t BR O , то есть за время
tn' t	tn''	хотя бы однажды точка A t попадает в круг BR O			или

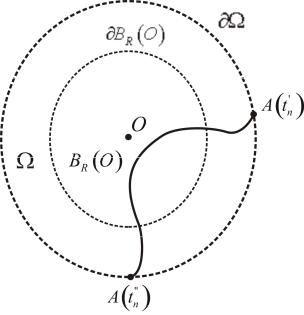
на его границу – окружность BR O (рис.5.3).

Обозначим через Tn полное время пребывания подвижной бро-

уновской точки внутри круга BR O в промежутке tn' t tn'' , яв-

ляющееся суммой длин интервалов пребывания, а через T обозначим Tn , конечную или бесконечную.

Если удовлетворяющий указанным выше условиям временной интервал tn' ,tn'' существует, то точка A tn'' находится на расстоя-

нии r от точки O. Следовательно, t tn'' вероятность возвраще-

ния A t в круг BR O равна . Поскольку A t с вероятностью единица не остается неограниченно долго на конечном расстоянии,

229

то утверждение, что подвижная броуновская точка A t возвраща-

ется в BR O равносильно утверждению о существовании интер-

вала tn' 1,tn'' 1 .

Рис.5.3. Движение подвижной броуновской точки A t в рамках

построений для доказательства теоремы 5.7

Таким образом, вероятность существования каждого последую-

щего интервала tn' ,tn'' при условии существования предыдущего

равна , следовательно, вероятность существования n -го интер-

вала равна n . Необходимо отметить, что даже, если существует интервал tn' ,tn'' , математическое ожидание Tn , согласно лемме 5.1,

имеет конечную верхнюю грань, не превышающую некоторого числа m. Следовательно, справедливо следующее соотношение:

T Tn	m n .	(5.12)
n	n

230

С другой стороны, вероятность того, что точка A t при броунов-

ском движении находится внутри круга BR O определяется сле-

дующими соотношениями:

P A t BR O p t

1

A 0 Q

2

2 t

exp

2t

dS

(5.13)

BR O

mes BR O

R2

,

2 t

2t

t

где Q – текущая точка круга, по которому ведется интегрирование,

mes BR O R2 – мера открытого круга

BR O . Тогда справед-

ливо

T

p t dt .

(5.14)

0

Однако, если 1, то величина T

будет конечной в соответст-

вии с формулой (5.12). Таким образом, 1,

что и требовалось

доказать. Теорема доказана. ▲ Доказанная теорема хорошо демонстрирует необычайную

сложность кривой C, проходящей бесконечно много раз вблизи всякой точки плоскости. Величина OA t t также претерпевает сложные изменения в малом интервале 0,t0 , ибо процесс стохас-

тически не меняется при замене t t02 t , и кривая в окрестности любой точки обладает теми же свойствами, что и в окрестности начальной точки. Невозможно представить себе все эти бесконечно малые зигзаги. Исключительная сложность кривой плоского броуновского движения C хорошо подчеркивается словами П. Леви

«…Notre imagination se lassera plutót de conservoir que la nature de fournir …»1 [126] и иллюстрируется на рис. 5.4.

В завершении данного параграфа приведем формулировки некоторых основных теорем, относящихся к кривой плоского броуновского движения.

1 «… Наше воображение утомляется быстрее, нежели иссякает природа, питающая его …».

231

Теорема 5.8. Кривая C почти наверно является множеством точек с нулевой плоской мерой, то есть с нулевой площадью по Лебегу.

Теорема 5.9. Если кривая C выходит из данной точки, то вероятность ее попадания в другую заданную точку равна нулю.

Рис. 5.4. Траектория плоского броуновского движения, полученная с помощью компьютерного моделирования [8, 10]

Из данной теоремы следует, в частности, что вероятность повторного попадания кривой C плоского броуновского движения в точку A t , соответствующую некоторому произвольно заданному

значению времени t, равна нулю. Другими словами, вероятность того, что заранее заданная точка A t является двойной точкой

плоского броуновского движения, равна нулю. Следовательно, двойные точки почти наверное образуют на оси t множество меры нуль.

Необходимо отметить важный результат, относящийся к одномерной винеровской функции X t и сформулированный в виде следующей теоремы.

232

Теорема 5.10. Пусть X t – одномерная винеровская функция.

Данная функция, почти наверно ограниченная и не имеющая ограниченной вариации ни в каком интервале, обладает счетными всюду плотными множествами как минимумов, так и максимумов.

§7. Броуновское движение в пространстве

В трехмерном пространстве, тем более, в пространстве с большим числом измерений, свойства кривой C броуновского движения будут совершенно иными. Выражение (5.13) для p t заменя-

ется на аналогичное выражение, но содержащее множитель t 32 , так что интеграл от полученного выражения оказывается уже сходящимся.

Двумерный шар BR2 O заменяется трехмерным шаром BR3 O

объема V соответственно. Обозначим через n вероятность появ-

ления броуновской точки A t внутри шара BR3 O в течение ин-

тервала времени n 1,n . Если A t в некоторый момент времени

t, находящийся между моментами t n 1 и t n, достигает по-

верхности, то есть границы, BR3 O , то соответствующая условная вероятность найти данную броуновскую точку в момент времени t n внутри шара BR3 O , по меньшей мере (как вытекает из факта выпуклости шара) равна:

k P A t BR3 O A BR3 O 0.

Отсюда для безусловной вероятности данного факта справедливо

неравенство	P n k n и,	следовательно, выполняется соотноше-
ние n 1 k P n .		Тогда по лемме Бореля – Кантелли
n	n

почти наверное существует такое число N , что n N рассматриваемое событие больше не произойдет, то есть броуновская точка A t больше не войдет в область BR3 O . Таким образом, спра-

ведлива следующая теорема.

233

Теорема 5.11. Какова бы ни была рассматриваемая ограниченная область многомерного пространства Rd , d 3, все точки

A t , попавшие в , почти наверно лежат на конечной дуге кри-

вой броуновского движения C.

Следовательно, в данном случае кривая C является замкнутым множеством. Мера этого множества почти наверно равна нулю, а по теореме 5.11 и проекция рассматриваемого множества на любые плоскости также почти наверно имеют нулевые меры.

Если взять шар радиуса r, центр которого находится на расстоянии a r от начального положения подвижной броуновской точки A t , то вероятность того, что кривая C содержит внутрен-

ние точки данного шара будет непрерывной возрастающей функцией от ra , равной нулю при r 0 и равной единице при r a.

§8. Процесс Орнштейна – Уленбека

Для описания процесса классического броуновского движения в качестве альтернативы винеровскому процессу Л. Орнштейном и Дж. Уленбеком в 1930 г. был предложен однородный диффузионный процесс vt , названный впоследствии процессом Орнштейна – Уленбека [131]. Необходимо отметить, что позже в 1934 г., используя другие, чем в [131] методы, та же теория была выдвинута С.Н. Бернштейном [132] и А.Н. Колмогоровым [133].

Определение 5.5. Процессом Орнштейна – Уленбека называется гауссовский стационарный случайный процесс vt с нулевым ма-

тематическим ожиданием vt 0, дисперсией Dvt 2 1 e 2 t

и экспоненциально затухающей корреляционной функцией следующего вида:

v t,s 2 exp t s , 0.

Для вычисления указанных характеристик следует выполнить усреднение по начальным данным v0 процесса Орштейна – Уленбека со стационарной функцией распределения

234

			1				2
	p v0				exp		v0		.
							2	2
			2 2

Поскольку винеровский процесс, описывающий физическую модель Эйнштейна – Смолуховского броуновского движения, недифференцируем, то в теории модель Эйнштейна – Смолуховского частица, совершающая броуновское движение не имеет нигде конечной скорости. В подходе Л. Орнштейна и Дж. Уленбека основной случайной величиной является не координата, а скорость vt блуждающей частицы. При этом предполагается, что силу, действующую на взвешенную в среде частицу, можно разложить на две компоненты – систематическую (сила трения) и стохастическую – обусловленную случайными толчками молекул среды.

Таким образом, процесс Орштейна – Уленбека может быть также определен как решение следующего стохастического дифференциального уравнения (уравнения Ланжевена1) [134]:

mdvt vtdt dwt ,	(5.15)
где wt –винеровский процесс (так что dwt dt	– обобщенный слу-

чайный процесс белого шума), m, – некоторые положительные постоянные, причем m . Уравнение (5.15) приближенно описывает линейное (одномерное) броуновское движение свободной частицы, при этом vt интерпретируется, как было указано выше,

как скорость частицы, m – ее масса, vt – сила вязкого трения2. Второе слагаемое в правой части (5.15) соответствует именно случайной компоненте силы, появление которой обусловлено хаотическими толчками молекул среды, находящихся в тепловом движении. Данная компонента, как было указано выше, является основной причиной броуновского движения и описывается белым шумом dwt .

В приближении Эйншетйна – Смолуховского m 0 соответ-

ствующее уравнение Ланжевена будет иметь вид dXt dwt . Дан-

1Более подробно уравнение Ланжевена описано в приложении 6.

2Например, для сферической частицы радиуса a в силу гидродинамиче-

ской формулы Стокса коэффициент вязкого трения 6 a .

235

ный частный случай уравнения (5.15) приводит к выводу, что координата броуновской частицы

t

X t vt 'dt ' 1wt ,

0

то есть описывается винеровским процессом. Таким образом, как было указано выше, физической модели броуновского движения Эйнштейна – Смолуховского соответствует математическая модель

– винеровский процесс. В уточненной модели броуновского движения учитывается инерция взвешенной частицы, то есть считается m 0. Уточненная модель опирается на полное уравнение (5.15) и математической моделью в данном случае служит процесс Орнштейна – Уленбека. Учет инерции частицы приводит к конечности скорости броуновской частицы, но ее ускорение остается бесконечным вследствие того, что процесс Орнштейна – Уленбека (также как и винеровский процесс) является недифференцируемым. Для того, чтобы и ускорение броуновской частицы оказалось конечным, необходимо дальнейшее уточнение модели, учитывающее отличие случайной силы от идеализированного белого шума [134].

Необходимо отметить, что процесс Орштейна – Уленбека не имеет независимых приращений, то есть измерения скорости броуновской частицы коррелированны на непересекающихся временных интервалах [135].

В соответствии с теоремой Дуба [136] процесс Орштейна – Уленбека является единственным стационарным гауссовским марковским случайным процессом.

Стационарность процесса Орштейна – Уленбека и отсутствие независимых приращений отличают его от винеровского процесса. Винеровский процесс, как математическая модель броуновского движения в пространстве координат блуждающей частицы, получается из процесса Орштейна – Уленбека в результате предельного перехода , , так что 2 const (для стандартного

винеровского процесса 2 1 ). Таким образом, винеровский процесс соответствует описанию броуновского движения в пределе большой вязкости среды (сильное трение) и интенсивного шума.

Процесс Орштейна – Уленбека v при 0 t допускает каноническое представление

236

	v k uk ,
	k 0
где коэффициенты k	– независимые гауссовские случайные вели-
чины такие, что k	0; k l k kl , k – собственные числа,

uk – собственные функции интегрального оператора с ядром

v t,s 2 e t s , определяемые в соответствии с уравнением

t

ds v t,s uk s kuk .

0

Процесс Орнштейна – Уленбека является однородным по времени марковским процессом диффузионного типа. Верно и обратное утверждение: процесс vt , являющийся одновременно стационарным случайным процессом, гауссовским процессом и марковским процессом, обязательно представляет собой процесс Орнштейна – Уленбека. Как марковский процесс рассматриваемый процесс Орнштейна – Уленбека удобно характеризовать его переходной плотностью p t, x, y , представляющей собой фундамен-

тальное решение прямого уравнения Колмогорова (4.16), которое в данном случае имеет следующий вид:

p 2 2 p yp .t y2 y

Таким образом, переходная плотность одномерного процесса Орнштейна – Уленбека задается формулой

			1				y	x e	t		2
	p t, x, y
						exp						.
		2 2	1 e 2 t		2		2 2 1 e 2 t

Необходимо отметить, что многие свойства процесса Орнштейна – Уленбека (включая марковость) можно вывести из соответствующих свойств винеровского процесса, воспользовавшись тем, что процесс

	t		ln t
w t		v
				2

237