Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

2) при фиксированных t и функция t, x, является A -

измеримой функцией точки x;

3) t, x, 1;
4) t, x, \ x 0;
5) t s, x, s, x,dy t, y, ,	s,t 0 .
Из условий 3) и 5) следует, что t 0, s 0		справедливы со-
отношения t s, x, s, x,dy s, x, .		Отсюда следует,

что переходная функция является невозрастающей функцией от t и существует предел 0, x, .

Определение 3.61. Переходная функция t, x, называется нормальной, если x : 0, x, 1.

Определение 3.62. Переходная функция называется консервативной, если t 0, x : t, x, 1.

Пусть A – пополнение -алгебры A по системе всех конечных мер . Каждая мера t, x, однозначно продолжается на -

алгебру A. При таком продолжении получается переходная функ-

ция1 в фазовом пространстве ,A . Поэтому, всюду, где это

удобно, можно считать, что A A.

Определение 3.63. Пусть – некоторая мера в фазовом про-

странстве ,A . Функция p t, x, y , где t 0, x, y называется переходной плотностью, если выполнены следующие условия:

1)t 0, x, y : p t, x, y 0;

2)при фиксированном t функция p t, x, y является A A - из-

меримой функцией двух переменных x, y ;

3) t 0, x : p t, x, y dy 1;

1 Подробнее – см. упражнение 16 в разделе «Упражнения».

158

4) s,t 0, x, z : p s t, x, z p s, x, y p t, y, z dy.

Пусть p t, x, y является переходной плотностью, тогда форму-

ла

	p t, x, y dy, при t 0;
t, x,
	x ,	при t 0
определяет переходную функцию		t, x, для множества	.

1, x ;

Здесь x , A, x – индикатор множества (или

0, x

характеристическая функция). Определенная таким образом переходная функция будет нормальной, если для x выполнено ра-

венство lim		p t, x, y dy 1, и консервативной, если		для t 0 и
t 0
	E
x справедливо			p t, x, y dy 1. Доказательство	данных ут-

E

верждений предоставляется читателю1.

Ниже подробно рассматриваются примеры некоторых важных переходных функций.

Пример 3.3.

Пусть – конечное или счетное множество, A – совокупность всех подмножеств данного множества, и пусть pij t , где t 0, i, j представляет собой набор функций, удовлетворяющих следующим условиям:

1)pij t 0;

2)pij t 1;

j

3) pij 0 0 при i j;

1 Подробнее – см. упражнение 17 в разделе «Упражнения».

159

4) для s,t 0, i, j,k : pij s pjk t pik s t .

j

Тогда формула

t, x, pxy t , x , t 0,

y

определяет переходную функцию, для которой условия нормальности и консервативности можно записать, соответственно, в сле-

дующей форме: pij 0 1, i и pij t 1, i .

j

j

Пример 3.4.

Пусть ,A является фазовым пространством, и пусть функ-

ция x, , x , A удовлетворяет следующим условиям:

1)x : x, – вероятностная мера на A;

2)A : x, – A -измеримая функция на .

Для целых n 0 определим набор функций n x, следующим

образом: 0 x, x , n 1: n x, x,dy n 1 y, .

Положим
		n	n
t, x,		t		e t n x, ,	(3.21)
	n!
n 0

где – некоторая положительная константа. Можно показать, что ряд в правой части выражения (3.21) сходится и определяет переходную функцию, соответствующую некоторому распределению вероятностей.

Определение 3.64. Переходная функция t, x, , определен-

ная формулой (3.21), называется переходной функцией Пуассона. Данная переходная функция может использоваться в различных

приложениях, для которых оказывается применимым, в частности, распредление Пуассона.

Пример 3.5.

Пусть – числовая прямая, то есть R1, A является - алгеброй, порожденной совокупностью всех интервалов на данной прямой, v – некоторая постоянная. Формула

160

t, x, x vt

(3.22)

задает консервативную переходную функцию.

Определение 3.65. Говорят, что переходная функция t, x, ,

определенная формулой (3.22), соответствует равномерному движению со скоростью v.

Пример 3.6.

Пусть – n -мерное евклидово пространство, A является - алгеброй всех борелевских множеств данного пространства, x, y – n -мерные вектора в рассматриваемом евклидовом пространстве: x, y . Положим

p t, x, y 2 t n 2 exp x y 2 2t .		(3.23)
Можно проверить, что функция p t, x, y ,	определенная выше, яв-
ляется переходной плотностью (по отношению к мере Лебега)1.
Определение 3.66. Функция p t, x, y ,	определенная формулой

(3.23), называется винеровской переходной плотностью или переходной плотностью винеровского случайного процесса.

Контрольные вопросы

1. Дайте определения основных типов случайных процессов. 2. Дайте определение переходной функции (плотности).

Рекомендуемая литература

3.1 2. Колмогоров А.Н. Основные понятия теории вероятно-

стей. М., 1974.

3.2.Феллер В. Введение в теорию вероятностей и ее прило-

жения. М., 1984.

1 В приведенной формуле (3.23) множитель x y 2 означает скалярный

квадрат (в общем случае, с произвольной размерностью) вектора x y .

2 Данная монография будет полезна для более углубленного изучения аксиоматического подхода в теории вероятностей.

161

Глава 4

МАРКОВСКИЕ ПРОЦЕССЫ

В данной главе более подробно рассматривается один из наиболее важных типов случайных процессов, а именно, марковские процессы и инфинитезимальные операторы. Представлено также математическое описание процессов диффузии как частного случая марковских процессов.

§1. Марковские процессы и марковские семейства

Пусть имеется измеримое пространство X ,B , в котором все

одноточечные множества измеримы. Данное пространство будем называть фазовым пространством. Соответственно, точки фазового пространства будем называть состояниями. Необходимо подчеркнуть, что терминология взята из физики; значение случайной функции t , t T интерпретируется как состояние, в котором находится некоторая физическая система в момент времени t.

1. t : ,F, P X ,B . Рассмотрим -алгебры, связанные с данной случайной функцией. Введем -алгебру, порожденную случайной функцией t , t T – наименьшую -алгебру, содержа-

щую все события следующего вида: t B , t T, B B. Обозна-

чим данную -алгебру через FT (или через Ft , t T в случае, если

необходимо будет указать к какой именно случайной величине данная наименьшая -алгебра относится). Таким образом, можно записать следующее равенство:

FT T , t T t B , t T , B B .

Рассматриваемая -алгебра имеет смысл совокупности всех событий, о наступлении которых можно узнать, наблюдая случайную функцию t , t T.

162

2. Если T R1, то есть если речь идет о случайном процессе, мы будем рассматривать также следующие -алгебры:

F t s , s T, s t ; F t s , s T, s t ;

Fs,t u , u T, s u t ;

F t t .

Необходимо отметить, что последняя, из указанных выше, - алгебра состоит из всех событий t B , B B.

Замечание. На языке теории вероятностей, если какое-либо свойство выполняется для каждой точки множества, исключая, быть может, лишь множество меры нуль, то говорят, что данное свойство выполняется на данном множестве «почти всюду» или «почти наверное».

1.1. Определение марковского процесса
Определение 4.1. Случайный процесс					t называется марков-
ским, если для любого t T и для любых					A F t , B F t		почти на-
верное выполняется следующее равенство:
P AB		F t P A		F t P B		F t .	(4.1)

Необходимо отметить, что в силу симметрии определения (4.1) из того факта, что t , t T является марковским процессом вытекает, что тот же случайный процесс с обращенным направлением времени, то есть t , t T, также является марковским.

Определение 4.2. Марковский процесс, определенный на множестве T называется цепью Маркова (или марковской цепью).

Определение 4.3. Цепью Маркова с непрерывным временем называется марковский процесс, для которого множество X является конечным или счетным, T 0, или T , 1.

1 Более подробно определения и описания для марковских процессов и цепей представлены в [117].

163

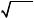
Частным случаем марковского процесса является винеровский случайный процесс и справедливо следующее определение на основе понятия марковского процесса [118].

Определение 4.4. Винеровским процессом называется однородный марковский процесс wt , t 0, для которого wt 0 0 и пере-

ходная плотность p t, x, y есть фундаментальное решение пара-

болического дифференциального уравнения

p

1 2 p

2 x2

t

и задается формулой

1

x y 2

p t, x, y

exp

.

2t

2 t

Обобщение на многомерный случай дается формулой (3.23). Важно отметить, что стандартный винеровский процесс являет-

ся марковским процессом wt со следующими свойствами:

а) wt 0 0, wt ws 0, D wt ws t s, t s;

б) для любых двух непересекающихся временных интерваловt1,t2 и t3 ,t4 , t1 t2 t3 t4 приращения wt4 wt3 и wt2 wt1 – независимые случайные величины со свойствами, указанными в предыдущем пункте. Аналогичное свойство имеет место и для n непересекающихся интервалов. Свойство независимости приращений позволяет использовать винеровский процесс для построения описания любых диффузионных процессов, в частности, броуновского движения.

Пример 4.1.

Необходимо отметить, что одним из важнейших примеров марковского процесса в физике является броуновское движение – движение малой частицы в жидкости под действием (ударами) молекул среды.

Ввиду важности данного явления для дальнейшего изложения, рассмотрим броуновское движение как марковский процесс более подробно.

В качестве фазового пространства состояний выберем простран-

ство R3,B3 . Если инерция частицы пренебрежимо мала, то опи-

164

сание случайных блужданий данной частицы при помощи марковского процесса оказывается достаточно точным: будущее движение частицы зависит только от положения (пространственной точки), которое она (частица) занимает в настоящее время, и не зависит от того, как и откуда частица попала в это положение. Данный вывод является следствием того, что удары молекул, которые предстоит испытать частице – это удары молекул, отличных от тех, которые ударяли ее в прошлом, или тех же самых молекул, но изменивших свое движение (и соответствующие параметры) в результате многочисленных столкновений.

В более сложном случае, когда нельзя пренебречь инерцией частицы (например, при движении одной молекулы в разряженном газе), уже нельзя считать изменение пространственных координатt , t , t протекающим в соответствии с марковским процессом.

В данном случае будущее движение зависит не только от положения частицы в данный момент времени, но также и от значения

скорости частицы t , t , t в настоящий момент времени. Но если ввести в рассмотрение фазовое пространство большего числа изме-

рений (размерности), а именно R6,B6 , то есть фиксировать по-

ложение частицы и ее скорости, то марковское приближение будет хорошо подходить и к данному случаю.

Пусть теперь броуновская частица находится не в жидкости, а в нагретом газе, и в определенный момент времени частица вспыхивает и сгорает (исчезает). Данный процесс может быть описан с помощью фазового пространства, измененного следующим образом.

Добавим к фазовому пространству R3,B3 , если рассматрива-

ется безынерционная частица, или к пространству R6,B6 , если

массой частицы не пренебрегается, соответственно, одну точку, обозначаемую ниже «*». Снабдим полученное пространство (без ущерба для общности далее будем рассматривать случай безмассо-

вой частицы) -алгеброй R3,B3 , * и будем в рамках иде-

альной модели считать, что частица, вместо того чтобы исчезать,

165

попадает в дополнительное состояние «*» и остается там навсегда. Очевидно, что при этом выполняется следующее равенство:

P s,*,t, * ,

где * – -функция Дирака.

Таким образом, при помощи введенного специальным способом дополнительного состояния удается избежать рассмотрения марковских процессов, определенных лишь до какого-то случайного конечного момента времени.

Замечание. Необходимо отметить, что в [115, 116] приняты и использованы другие определения, согласно которым марковский процесс может быть определен лишь до некоторого случайного конечного момента времени, в котором он обрывается; это условие усложняет соответствующие определения, но позволяет обойтись без введения дополнительного состояния для процессов с исчезновением частицы. При такой концепции процессы, обрывающиеся с положительной вероятностью, называются неконсервативными.

1.2. Марковские семейства случайных процессов

Для дальнейшего рассмотрения необходимо ввести переходную функцию марковского процесса.

Определение 4.5. Говорят, что функция P s, x,t, , опреде-

ленная для всех s,t T : s t; x X ; B, является переходной

функцией марковского процесса t , t T, если выполняются следующие условия:

а) при фиксированных s, x,t функция P s, x,t, является веро-

ятностной мерой на -алгебре B, то есть справедливо

P s, x,t, X 1;

б) при фиксированных s, x, функция P s, ,t, измерима от-

носительно -алгебры B;

в) выполняется равенство P s, x,t, x , то есть функция

P s, x,t, – это мера, равная единице, когда x и нулю, в слу-

чае, если x ;

166

г) для любых s,t T : s t; x X ; B почти наверное выполняется следующее равенство:

P t p s, s ,t, .

Замечание. Необходимо помнить, что требования а) – в) налагаются только на функцию P , , , и не касаются случайного

процесса t , тогда как требование г) говорит о связи между

собой этих двух объектов.

Важно отметить, что основное внимание в теории марковских процессов уделяется однородным (по времени) марковским процессам. Для однородных марковских процессов переходная функция однородна, то есть зависит лишь от разности аргументов:

P s, x,t, P t s, x, .

Строгое формальное определение однородного марковского процесса достаточно громоздко [119] и не существенно для дальнейшего рассмотрения.

Понятие марковского семейства связано с представлением о возможности начать случайное движение системы в произвольно выбранной любой точке фазового пространства. В силу этого определение, приводимое ниже, будет достаточно сложным, но эта сложность оправдана.

Пусть фиксировано некоторое множество T на числовой оси и фазовое пространство X ,B и задана функция P s, x,t, , удов-

летворяющая условиям а) – в) определения 4.5. Пусть имеется пространство элементарных событий , на T задана произвольная

функция t , принимающая значения в X . Важно отметить, что

это еще не случайный процесс, так как на пространстве событий не только не определено никакой вероятностной меры, но даже еще и не задано никакой -алгебры. Поэтому свяжем с данной функ-

цией t -алгебры FT ,F t ,F t ,Fs,t , определенные выше. Далее предположим, что s T и x X на -алгебре F s определена вероятностная мера Ps,x .

167