Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

4) для почти всех функция Bt непрерывна по t.

Таким образом, на качественном уровне классический процесс броуновского движения B t можно определить как начинающий-

ся в начале координат случайный процесс t , приращения которого на непересекающихся интервалах времени t являются независимыми и величины этих приращений имеют гауссово распределение. Дисперсия данного процесса определяется формулой

2 D t,

где 2Kd – коэффициент диффузии.

Марковское свойство. Броуновское движение, как и любой случайный процесс с независимыми приращениями, является марковским процессом. Это означает, что условная вероятность следующего события «B t2 достигает определенного значения при за-

данном значении B t1 », где t1 t2 зависит только от t1 и t2. Дан-

ная условная вероятность не зависит от поведения B t при t t1,

то есть в процессе случайного блуждания каждый шаг делается без какой-либо информации о том, каким именно образом процесс достигает текущего значения. Учитывая формальные определения и свойства марковского процесса и марковского семейства, приведенное выше утверждение для броуновского движения можно за-

писать как t1 tk : P B tk xk B tk 1 xk 1, ,B t1 x1

P B tk xk B tk 1 xk 1 .

Абсолютная величина приращений.

Теорема 5.1. Пусть B t – броуновское движение на отрезке

a,b . Тогда математическое ожидание модуля приращения равно:

2

M B t2 B t1 t2 t1 .

Доказательство. Если случайная величина имеет плотность

вероятности f t , то математическое ожидание функции случай-

208

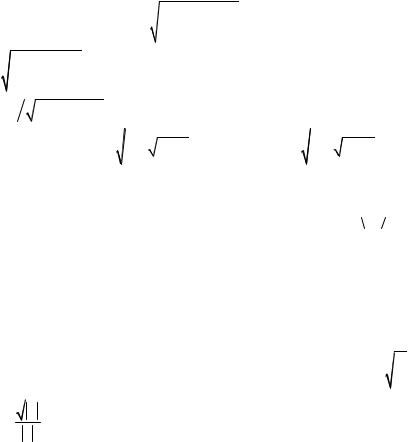
r

r t f

t dt. Соответст-

ной

величины

равно:

M r

венно, при t2 t1

для приращения броуновского движения справед-

u2

B t2 B t1

1

ливо

M

u

du

2

exp

2

2

t2

t1

2

t2 t1

u

2

2

u

exp

du. Используя подстановку

2

2

t2 t1

0

2

t2 t1

s u

2 2 t2 t1

и необходимые упрощения,

можно получить

2

2

B t2 B t1

2s exp s

2

ds

M

t2 t1

t2 t1 . Тео-

0

рема доказана. ▲ В соответствии с данной теоремой среднеквадратичное смеще-

ние броуновской частицы возрастает линейно во времени ( 2 t -

см. выше). Такая скорость роста характерна для процесса диффузии.

Недифференцируемость. Из доказанной теоремы 5.1 следует недифференцируемость броуновского движения B t в каждой

точке t a,b . Предположим, что существует

B' t . Тогда, рассу-

B t h B t

ждая нестрого, можно получить

B ' t

def

2

lim

h

h 0

h

lim . Таким образом, траектория винеровского процесса,

h 0 h

с вероятностью равной единице, является нигде не дифференцируемой функцией, то есть скорость броуновской частицы не определена. Это обстоятельство является идеализацией, отражающей тот факт, что траектории реальной броуновской частицы сильно «нерегулярные» и не могут быть прослежены в деталях.

209

Важно отметить, что в [129] представлено полное доказательство не только для классического, но также и для обобщенного (фрактального) броуновского движения, рассматриваемого ниже.

Масштабная инвариантность. Из (5.1) следует, что траектория классического винеровского процесса – броуновского движения – B t обладает свойством масштабной инвариантности или скей-

лингом. Действительно, для плотностей вероятностей процессов B t и b 12 B bt при любом коэффициенте b 0 справедливо следующее соотношение:

				1 2
		b , b b			p , ,	(5.2)
	p

которое означает инвариантность рассматриваемых процессов в смысле распределения. Соотношение (5.2) показывает, что график броуновского случайного процесса относится к классу самоаффинных фрактальных функций1. Вероятностные свойства броуновского процесса не изменяются при одновременном изменении масштаба временной переменной в b раз и масштаба пространственной пе-

ременной в b раз.

Статистические свойства

Вероятностные (статистические) характеристики броуновского движения могут быть описаны в терминах распределения вероят-

ностей max ws :

0 s t

P max w a

2P w

a

2

dx exp

x2

,

0 s t

s

s

t

2t

a

где 0 a , t – фиксировано; или в терминах распределения ве-

роятностей времени 0	достижения винеровским процессом фик-
сированной точки a 0 в		рассматриваемом								(одномерном) про-
странстве:
				a	t			x	2
P a	t	2
						dx exp				,
								2t
					0

где 0 t , a – фиксировано.

1 Строгие определения и подробное рассмотрение самоаффинных функций представлено в данной главе ниже.

210

Размерность реализации. Результат теоремы 5.1 может быть использован для вычисления фрактальной размерности реализации броуновского движения B t . Без потери общности можно счи-

тать, что областью определения B t является 0,1 . Данный отре-

зок делится на n равных частей, длина каждой составляет t 1n. Ось ординат OY декартовой прямоугольной системы координат также делится на отрезки соответствующей длины t. ОтношениеB 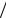t служит в качестве оценки числа квадратов со стороной t,

необходимых для покрытия части графика функции y B t , рас-

положенной над одним из фиксированных отрезков по оси абсцисс

Ot длиной t. В силу того, что M B t, число необходи-

мых	квадратов для одного	отрезка	N1 1	t . Всего имеется
n 1	t отрезков по оси Ot,	и поэтому общее число необходимых
квадратов N t t 3 2 .		Учитывая	определение фрактальной

размерности [1], можно получить для размерности реализации

	классического		броуновского движения		следующее значение:
		log N t
	d lim			1,5. Отсюда видно,	что реализация даже
		log t
	t 0

классического броуновского движения представляет собой кривую с дробной размерностью, то есть обладает фрактальными свойствами.

Статистическое самоподобие. Приращение реализации бро-

уновского движения B t обладает свойством статистического са-

моподобия, то есть r 0 справедливо следующее соотношение:

	1			1
B t t B t			B t r t B t .
		r

1 Символ означает, что две случайные величины имеют одинаковое распределение и, в частности, одни и те же математические ожидания и дисперсии.

211

Для доказательства представленного равенства необходимо доказать, что

P				P						(5.3)
	B t t B t		x		B t r t B t			rx .

По свойству 2) определения броуновского движения левая часть

(5.3) равна: P B t t B t x			1	x			s	2
					exp					ds,
			2 2 t				2 2		t

1

rx

2

а правая –

exp

s

ds.

Выполняя замену пере-

2

2

t

2 r

2r

t

менных s u

во втором интеграле, можно свести его к преды-

r

дущему интегралу. Свойство доказано.

Важно отметить, что случайный процесс, являющийся обобщенной производной по времени от броуновского движения, то есть производной от винеровского процесса, называется процессом гауссовского белого шума gt dwt 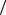dt. Гауссовкий белый шум служит основой для построения стохастических диффузионных процессов Y t , «управляемых» стохастическими дифференци-

альными уравнениями1, записанными в форме дифференциалов:

dY t a t,Y t dt b t,Y t dwt .

Резюмируя изложенное выше, можно утверждать, что рассмотренное классическое броуновское движение представляет собой хорошую модель марковских случайных фракталов, для которых,

как было указано выше,	условная вероятность того, что B t2			дос-
тигает определенного значения при заданном значении		B t1	,	где
t1 t2 зависит только от	t1 и t2 , а не от поведения B t	при t		t1.

Представляется достаточно очевидной необходимость введения такого случайного процесса, который обладал бы некоторой памятью. Такой процесс получил название обобщенного (фрактального) броуновского движения и был впервые исследован в 1968 г. [129]. Важно отметить, однако, что фрактальное броуновское дви-

1 Одним из наиболее известных примеров стохастических дифференциальных уравнений является уравнение Ланжевена (см. ниже).

212

жение в неявном виде рассматривалось А.Н. Колмогоровым еще в 1940 г. [125]. Вследствие важности, в том числе и для приложений в фундаментальной физике процесс фрактального броуновского движения будет рассмотрен более подробно ниже.

§3. Траектория линейного броуновского движения

Случайный – винеровский – процесс, который в дальнейшим будет называться «линейное броуновское движение», есть матема-

тическая модель, хорошо передающая свойства реального физического броуновского движения, наблюдаемого на достаточно малой (но не бесконечно малой) временной шкале и предполагающая, что такие же свойства имеют место на любой шкале. В данном случае исчезает понятие свободного пробега, в течение которого движение отдельной произвольно выбранной частицы (молекулы), рассматриваемое независимо от движения других частиц, является существенным образом прямолинейным и равномерным. Каждая частица (молекула) за конечное время пробегает бесконечный путь, а любая из ее координат есть функция, не имеющая производной и принимающая бесконечное число раз максимальные и минимальные значения в любом интервале.

Исключительно важно отметить наличие свойства принципиального подобия процесса на различных временных и пространственных (то есть при рассмотрении траектории движения с различным пространственным разрешением) масштабах. Данное свойство является неотъемлемой и важной характеристикой фракталов [1]. Таким образом, уже на данном этапе можно говорить о глубокой взаимосвязи случайных (стохастических) процессов, в частности, рассматриваемого линейного броуновского движения1 и таких важнейших понятий современной математики как «фрактал»,

«фрактальное множество», «фрактальная геометрия». Очевид-

но, указанная взаимосвязь просматривается пока на интуитивном, понятийном уровне, однако, при дальнейшем рассмотрении данные

1 Данный тип случайных (стохастических) процессов является простейшим случаем броуновского движения, а именно, одномерным классическим броуновским движением. Обобщенное броуновское движение будет рассмотрено ниже.

213

свойства случайных процессов будут рассмотрены подробно и установлены строго.

При изучении линейного (одномерного) броуновского движения рассматривается только одна координата, обозначаемая, например X . Соответственно, винеровский процесс, являющийся моделью реального физического процесса броуновского движения, в данном случае и для удобства последующего геометрического рассмотрения кривых броуновского движения при большем числе измерений можно обозначить X t .

Таким образом, далее (если специально не оговорено) будем рассматривать только одну из координат X t .

Замечание. Если в определении 5.2 (с учетом новых обозначений) заменить требование X 0 0 на условие X 0 x0, получа-

ется определение винеровского процесса, выходящего из некоторой произвольной начальной точки x0 , отличной от нуля. В дальнейшем будет выполнено рассмотрение одновременно всех винеровских процессов, выходящих из разных начальных точек, что является примером марковского семейства случайных процессов.

Выпишем конечномерное распределение винеровского процес-

са. Для последовательности 0 t1 t2 tn совместное распре-
деление случайных величин	X t1 , X t2 , , X tn будет иметь
плотность распределения вероятностей pt1 t2 tn . Случайный вектор
X t X t1 , X t2 , , X tn	получается с помощью невырож-
денного линейного преобразования A, которое действует на слу-

чайный вектор приращений, имеющий, в свою очередь, следующий вид:

X

X t X t

0

0

, X t

2

X t

, , X t

n

X t

n 1

1

1

и плотность распределения вероятности:

n

1 2

2

p

x , x

, x

2 t

t

exp

xi

.

X

t

t

1 2

n

i

i 1

2

i

i 1

i 1

214

Для вычисления рассматриваемой плотности распределения вероятностей pX t1 X tn можно воспользоваться следующими свойст-

вами:

а) пусть вектор X получается из вектора линейным невы-

рожденным преобразованием A, то есть X A . Тогда плотность распределения вероятностей вектора X , полученного из случайного вектора линейным невырожденным преобразованием, определяется следующей формулой:

pA x det A 1 p A 1x , x x1, x2 , , xn ;

б) тот же результат можно получить, если использовать условные плотности распределений.

§4. Кривая плоского броуновского движения

Определение 5.4. Пусть R2		– координатная плоскость. Кри-
	x1 ,x2
вой C плоского броуновского движения называется траектория
подвижной точки A t		2
	(или просто A ) на плоскости Rx1 ,x2 с коор-
динатами X1 t , X2 t ,	являющимися независимыми случайными

функциями линейного броуновского движения, то есть независимыми винеровскими функциями.

Пусть параметр t 1 возрастает от некоторого начального значе-

ния t0 , принятого за нуль и для которого Xi t0 0 0, i 1,2, на

некоторую величину . Тогда перемещение точки A представляется вектором

R X1 , X2 ,

распределенным по изотропному (или, как еще говорят, круговому) нормальному закону с параметром, определенным согласно следующей формулы:

			2	X2	2		2 ,	(5.4)
R2 X	1

1 В физическом смысле и для случайных процессов, как было указано выше, параметр t – это время.

215

где i 1,2 : Xi Xi Xi 0 . Отсюда следует, что если ввести длину перемещения стандартным образом R t R t , то

P R t t exp 2 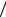2 0 . (5.5)

4.1. Построение кривой плоского броуновского движения

Выполним построение кривой C с помощью последовательно-

сти интерполяций.

Пусть

A0 A t0 , A1 A t1 .

Тогда

t t0 ,t1

положение точки A t определяется следующим образом:

t1 t

OA0

t t0

OA1

OA

t v,

(5.6)

t1

t0

где

t

t t0 t1 t

и вектор v

– приведенный лапласов век-

t1 t0

тор, то есть вектор, распределенный по изотропному нормальному

закону, определенному согласно (5.5), при t 1:	P		v
exp 2 2 , 0.

Действительно, для каждой компоненты вектор-функции OA t

данные интерполяции приводят к построению случайной траектории линейного броуновского движения (подробнее см. выше §3). Из результатов, полученных выше, для линейного броуновского движения, следует, что предложенный алгоритм построения приводит к почти наверное непрерывной кривой, а коэффициент кор-

реляции между векторами OA0 и OA1 (при условии, если O A 0

и 0 t0

t1 ) определяется следующим образом:

M OA0 OA1

M X1 t0 X

1 t1 X

2 t0 X

2 t1

t

0

.

2

M

2

2 t0t1

t1

M

OA0

OA0

Рассмотрим расстояние R OA . Для каждого заданного значения

параметра t величина R t распределена по закону, определяемо-

216

му согласно (5.5). Пусть задана последовательность tn , для кото-

рой n,n 1,2, :tn t0qn ,q 1, то есть последовательность значений параметра времени t, растущих в геометрической прогрессии. Тогда возможные значения отношения

n R tn

tn

осуществляются с частотами, при n почти наверное стремящихся к своим теоретическим вероятностям. Более точно, посколь-

ку координаты вектор-функции OA t X1 t , X2 t независимы одна от другой, различные возможные значения отношения n очень вероятно будут реализовываться с частотами, почти пропорциональными их теоретическим вероятностям. Это следует из того, что при большой разности n n ' величины OAn и OAn ' , а следо-

вательно, и величины n и n ' почти независимы. Таким образом,

в последовательности n каждый член существенно коррелиро-

ван только с конечным числом соседних членов1. В данных условиях справедлив закон больших чисел, из которого следует справедливость следующей теоремы.

Теорема 5.2. Частота появлений значений n , превышающих некоторое фиксированное значение , почти наверное стремится к теоретической вероятности (5.5).

Из данной теоремы следует, что усреднение случайной величины (или 2 ) по логарифмической шкале t почти наверное приводит к теоретическому среднему, то есть к соответствующему математическому ожиданию, определяемому из формулы (5.5) и рав-

ному 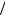2 в случае , или 2 для 2 .

Для величин tn , растущих в арифметической прогрессии, или для средних по t аналогичные приведенным выше утверждения

1 Точнее говоря, коэффициенты корреляции убывают в геометрической прогрессии по мере того как увеличивается удаление между коррелируемыми членами последовательности.

217