Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

Определение 4.6. Говорят, что упорядоченный набор элементов

t , Ps,x является марковским семейством с переходной функ-

цией P s, x,t, , если s, x выполнены следующие условия:

а) случайный процесс t , t T s, на вероятностном пространстве ,F s , Ps,x является марковским;

б) данный марковский процесс обладает указанной выше переходной функцией, а именно P s, x,t, ;

в) справедливо равенство Ps,x s x 1.

Более подробно, от семейства процессов t , t T 0, на вероятностных пространствах ,F s , Ps,x требуется следующее.

Во-первых, это должно быть семейство марковских процессов, то есть для любых s, x,t s; A Fs,t , B F t почти наверное Ps,x должно выполняться следующее равенство:

Ps,x AB t Ps,x A t Ps,x B t .

Необходимо отметить, здесь берутся условные вероятности, соответствующие исходной вероятностной мере Ps,x на -алгебре F s ;

соответственно, мы должны пояснить, относительно какой вероятностной меры почти наверное имеет место равенство.

Во-вторых, рассматриваемое семейство процессов должно быть семейством марковских процессов с общей переходной функцией P , , , , то есть для s t u из T , для любого x X и для лю-

бого из B почти наверное Ps,x должно выполняться следую-

щее равенство:

Ps,x u Fs,t P t, t ,u, .

Необходимо подчеркнуть, что данное выражение не зависит не только от поведения процесса на отрезке s,t , за исключением последней точки, но также и от s, и от x.

Требование в) определения 4.6 не нуждается в более подробной расшифровке: оно означает, что вероятность Ps,x берется в предпо-

168

ложении, что процесс в момент s выпускается из точки x (с этим связано также то, что рассматривается процесс только на значениях t s и берутся события только из -алгебры F s ).

Пример 4.2.

Рассмотрим семейство винеровских процессов, выходящих из всевозможных начальных пространственных точек, – марковское

семейство t , Ps,x		с плотностью вероятностей перехода (в n -
мерном случае)			n 2 exp
p s, x,t, y	2 t s					y x		n 2	t s	,

то есть с переходной функцией

P s, x,t, 2 t s n2 exp y x t s dy.

Учитывая определение условных вероятностей относительно -алгебры, можно записать следующую интегральную форму, справедливую A Fs,t :

Ps,x A u P t, t ,u, Ps,x d .

A

Из данного выражения, если вместо A взять все пространство элементарных событий , положить t s, а вместо u взять t, можно получить следующее равенство:

Ps,x u P s, s ,t, Ps,x d .

В силу того, что почти наверное для Ps,x справедливо равенство

Ps,x s x 1, то подынтегральная функция почти всюду равна

P s, x,t, . Значит, выполняется следующее равенство:

Ps,x s P s, x,t, .

Соответственно, из последнего равенства следует, что в случае марковского семейства, а не отдельного марковского процесса, переходная функция определяется однозначно (а не почти однозначно).

Замечание. Эту же самую идею о возможности выпустить марковский процесс из любой точки можно выразить другим спосо-

169

бом. А именно, можно рассмотреть семейство марковских процес-

сов ts,x , причем ss,x x; но вероятность P в данном слу-

чае можно взять не зависящей от x. На такой концепции строится изложение, например, в [120]. Как оказалось, семейства такого вида можно свести к марковским семействам.

1.3. Семейство операторов, связанное с марковскими процессами

Пусть X ,B является измеримым пространством. Свяжем с данным пространством два банаховых пространства. Первое, H, – банахово пространство всех ограниченных B -измеримых числовых функций f x , определенных на множестве X с нормой,

введенной согласно формуле	f x	sup	f x	. Необходимо от-
		X

метить, что сходимость в смысле указанной нормы является равномерной сходимостью. Второе, K, – банахово пространство всех счетно-аддитивных числовых функций множества1, определенных

на -алгебре B; в качестве нормы элемента

v K

возьмем его

полную вариацию на всем пространстве

v

v

X

[121]. Можно

показать, что для определенной таким образом

v

выполнены все

свойства нормы. Необходимо отметить, что банахово пространство K – полно [115]. Положим

v, f f v dx .

X

Отметим, что интеграл в данном выражении определяется следую-

щим образом: f x K dx f x K dx , где используется

X X

разложение Жордана v K K [121]. Можно записать следующие соответствия: v K : v v, – линейный функционал на

1 В литературе данные функции могут называться «обобщенными мерами», «мерами со знаком», или «зарядами». Более подробно – см. [120].

170

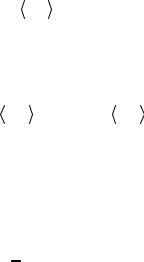
пространстве H, f H: f , f

– линейный функционал на

пространстве K. Таким образом,

получается естественное вложе-

ние пространства K в H*

(то есть в пространство, сопряженное

H), а H – соответственно, в K*.

Норма элемента и норма соответ-

ствующего линейного функционала совпадают друг с другом:

v

sup

v, f

;

f

sup

v, f

.

f x

1

v

1

Данное утверждение нуждается в доказательстве, которое авторы предоставляют читателю.

§2. Элементы теории групп

Типичной для марковских процессов является такая ситуация, когда известны переходные вероятности за малый промежуток

времени t с точностью до O t при t 0 и данной информа-

ции, при некоторых условиях регулярности, оказывается достаточно для того, чтобы восстановить всю переходную функцию. Ниже будет введен инфинитезимальный оператор, как раз такая характеристика, которая позволяет выполнять указанную процедуру, и затем будет показано, как данная характеристика связана с переходной функцией.

Пусть E – банахово пространство и пусть P t является линей-

ным ограниченным оператором таким, что P t :E E, t 0.

Определение 4.7. Семейство P t , t 0 линейно ограниченных операторов, действующих в E, называется однопараметрической полугруппой (или просто полугруппой), если s,t 0 справедливо следующее равенство: P s t P s P t .

Определение 4.8. Полугруппа P t , t 0 называется сжимающей,

если t 0 :	P t	1, то есть t 0, f E :	P t f		f	.

Определение 4.9. Пусть P t , t 0 является полугруппой линейных ограниченных операторов в банаховом пространстве E и пусть DA – подмножество в E. Оператор A : DA E называется

171

инфинитезимальным оператором, если f DA				limt 1 P t f f			и
f DA : Af limt 1 P t f f ,				t 0
	где сходимость является сходимо-
t 0
стью по норме рассматриваемого пространства E.
Из определения 4.9 следует,		что если – поле,			над которым
рассматривается линейное пространство E, то				f1, f2 DA и для
любых 1, 2 справедливы		соотношения:		1 f1	2 f2 DA		и
A 1 f1 2 f2 1Af1 2 Af2. Это означает, что DA					является ли-
нейным подпространством линейного пространства E, A – линей-
ный оператор и Af является (правой) производной P t f						в точке
«нуль»:
Af		d P t f	.
		dt
Определение 4.10. Инфинитезимальный оператор A,						связан-

ный с марковским семейством, называется инфинитезимальным оператором марковского семейства1.

Выше с любым марковским семейством были связаны два банаховых пространства H и K. Как было указано выше, норма в бана-

ховом пространстве H вводится как f H:		f	sup	f x	. Тогда
			x X
определение 4.9 для Af , f H можно переписать в виде
Af x limt 1 P t f x f x limt 1 x			f t f x ,
t 0	t 0
причем выполнено условие	f DA, если данный предел равноме-
рен по x.

Важно отметить, что полученная формула определяет инфинитезимальный оператор для однородного марковского процесса. Для

неоднородного марковского процесса t , Ps,x инфинитезималь-

ный оператор определяется следующим образом [122]:

At f x lim t ' t 1 t,x f t ' f x ,

t ' t

1 Иногда в литературе вместо термина «инфинитезимальный оператор» используют термин «производящий оператор».

172

причем вопросы существования и единственности в данном случае сложнее.

Пример 4.3.

С детерминированным процессом движения «вправо» с единич-

ной скоростью	на	прямой связана полугруппа			сдвигов
P t f x f x t .	Справедливо следующее равенство:
Af x limt 1 f x t f x			d f x	.	(4.2)
	t 0		dx

Однако не следует забывать, что указанная правая производная должна существовать равномерно по x.

Из того факта, что предел (4.2) существует равномерно по x,

следует равномерная непрерывность функции f x на X . Более того, функция t 1 f x t f x тоже является ограниченной и равномерно непрерывной, и равномерный предел d f x 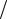dx огра-

ничен и равномерно непрерывен. Отсюда следует, что функция f x – дифференцируема не только справа, но и слева. На основе приведенных рассуждений можно сделать окончательный вывод, что подмножество DA банахова пространства E состоит из тех и только тех функций f x , которые ограничены и равномерно не-

прерывны вместе с первой производной, то есть f x Cравн1 , и для них Af x f ' x .

Пример 4.4.

Рассмотрим более подробно еще один важный детерминированный процесс, а именно, решение системы обыкновенных дифференциальных уравнений dxt 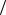dt b xt в r -мерном пространстве.

В данном случае не будем находить в точности область определения инфинитезимального оператора DA : заранее ограничим наше рассмотрение непрерывно дифференцируемыми финитными

функциями f x Cфин1	. Для функций данного типа при t 0 спра-
ведливо, что функция	f xt x f x b x t		t f x
		O

173

	r	f
			x bi x		t равномерно сходится по	x, f DA и дейст-
				O
		i
	i 1	x

вие инфинитезимального оператора на функцию определяется сле-

	r	f
	дующим образом: Af		x bi x .
		i
	i 1	x

Рассмотрим важное понятие, связанное с полугруппами и инфинитезимальными операторами, при этом ограничимся случаем сжимающей полугруппы на пространстве H ограниченных изме-

римых функций.
Введем в			H подпространство			H0, состоящее из функций, для
которых		P t	f f		0 при t 0.	Это функции, для которых полу-
группа P t		сильно непрерывна справа в нуле. Важно отметить, что

линейное подпространство H0 пространства H является замкну-

тым, а следовательно, H0 является банаховым пространством. До-

кажем этот важный факт.

Пусть имеется последовательность функций fn n 1 , для кото-

рой fn f

при n и n 1,2, : fn H0. Для данной после-

довательности функций справедливо следующее соотношение:

lim

P t f f

lim

P t f P t fn

lim

P t fn fn

fn f

.

(4.3)

t 0

t 0

t 0

Второй член в правой части неравенства (4.3) равен нулю, а для

первого слагаемого

P t f

P t fn

P t f

fn

f fn

. В

lim

lim

t 0

t 0

силу того, что норма

f fn

0 при n ,

то левая часть нера-

венства (4.3) равна нулю и f H0, что и требовалось доказать.

Оказывается, что если f H , то функция P t f ,

значения кото-

0

рой принадлежат банаховому пространству H0, равномерно непре-

рывна по

t

на всей полупрямой 0, , то есть

s,t 0, s t :

P t f P s

f

P s P t s f f

P t s f f

0 в пределе t s 0.

Отсюда, в частности, следует, что банахово пространство H0 будет

174

	инвариантно относительно оператора				P t : f H P t f H , так
							0	0
	как справедливо: P hP t f P h t		f P t f		при h 0.
	С инфинитезимальным оператором A пространство H0 связано
	следующим образом: D H		и f D : P t f H .					Известно, что
	A	0				A	0
	Af – правая производная P t f		в нулевой точке в смысле сильной
	сходимости. Докажем, что если f D ,						то P t f D и справедли-
	во следующее равенство:				A			A
				d
	AP t f	P t Af				P t f		(4.4)
				dt

в смысле той же сходимости.

По определению 4.9 справедлива следующая цепочка равенств:

AP t f limh 1 P hP t f	P t f limh 1 P t h f	P t f 1, то есть AP t f
t 0	t 0

– правая производная от P t f (важно отметить, что существование

AP t f равносильно существованию d P t f dt , и если они существуют, то равны). Воспользовавшись полугрупповым свойством еще раз можно получить P hP t f P t f P t h f P t f P t P h f f . До-

кажем, что limP th 1 P h f	f P t Af . С учетом того, что рассмат-
h 0

ривается сжимающее отображение справедливы следующие соот-

ношения:

t

h

1

P

h

f f P

t

Af

P

t

1

P

h

f f Af

P

h

h 1 P h f f Af 0 при h 0. Для того, чтобы доказать спра-

ведливость (4.4) осталось доказать, что и левая производная от

P t f равна тому же выражению. Действительно, справедливо

h 1 P t h f P t f P t Af P t h h 1 f P h f P t h Af

P t h Af P t Af . Первое слагаемое в правой части данного нера-

1 Второе равенство выполняется согласно полугрупповому свойству.

175

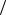
венства не превосходит	h 1 P h f f Af	0 при	h 0; второе
слагаемое стремится к нулю в силу того, что Af H0.			Таким обра-
зом, справедливость (4.4) доказана.
Замечание. Если обозначить P t f через u , то для u получаем
дифференциальное уравнение dut dt Aut		t	t
		с начальным условием

u0 f .

Переводя (4.4) в интегральную форму, можно получить

t	t
P t f f AP s fds	f P s Afds.	(4.5)
0	0
Для полугрупп на пространстве	H, связанных с марковскими
семействами, имеет место очень важный принцип.		f x имеет
Теорема 4.1 (принцип максимума). Если функция

абсолютный максимум в точке x, то есть y X : f x f y , и

f DA, то Af x 0.

Для любого марковского семейства t , Px имеем выполнение

неравенства x f t f	x . Отсюда следует справедливость сле-
дующего соотношения: Af x limt 1 x f t f x 0.
	t 0
Определение 4.11. Резольвентой полугруппы		операторов P t
называется семейство операторов R , определяемых формулой
R f	exp t P t fdt.	(4.6)
	0

Данная формула представляет собой преобразование Лапласа полугруппы P t .

В силу важности, уточним это определение. Интеграл (4.6) можно определить для полугруппы в любом банаховом пространстве, но в данном случае рассмотрение ограничится случаем пространства H, определенном выше.

Пусть t ,0 t ; Px – марковское семейство, причем про-

цесс t прогрессивно измерим относительно семейства -алгебр

176

F	. Тогда функция P t f x	измерима по t, x для любой функции
t			f x H, x X справедливо выраже-
f H. Предположим, что для
ние (4.6), то есть

R f x exp t P t f x dt.

0

Данный интеграл сходится, во всяком случае при 0 1. Сходи-

мость следует из неравенства	P t f x		f x	.	Функция R f x

является измеримой (по теореме Фубини) и ограниченной в силу

справедливости следующего неравенства:			R f x						1	f x	,
то есть R f x H.
Представляется достаточно очевидным,	что R , 0 являются
линейными операторами и они ограничены:		R					1.

Определение 4.12. Семейство R называется резольвентой по-

лугруппы P t или соответствующего марковского семейства.

При любом x X функция R f x	является преобразованием
Лапласа функции P t f x , t 0, .	Знание R f x при всех

0 позволяет восстановить функцию P t f x , t 0 с точностью до функции, отличной от нуля лишь на множестве значений t ле-

беговой меры «нуль» [121, 123]. Если f H ,		то функция P t f x
	0
непрерывна по t	и она восстанавливается	на	основе знания
R f x при всех	0 в точности однозначно.		Отсюда следует
очень важный вывод: по резольвенте R f x ,		известной при всех

0, однозначно восстанавливается полугруппа P t на простран-

стве H0 ее сильной непрерывности.

Пусть пространство H0 содержит достаточно много функций – настолько много, что из справедливости равенства нулю скалярно-

1 В рамках данной главы мы не будем рассматривать резольвенту при комплексных .

177