Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

Формальный подход пКХД, указанный выше, также предсказывает логарифмические поправки. В данном случае, учитывая соотношения (1.19) и (1.37), моменты несинглетных по аромату комбинаций структурных функций нуклона изменяются в зависимости от квадрата переданного 4-импульса согласно формуле

F

NS

n,Q

2

F

NS

n,Q

2

s Q2 dn

.

i

i

0

s Q02

Величина dn положительна при

n 1,

отрицательна при n 1 и

равна нулю при n 1, то есть с ростом Q моменты высоких рангов убывают, моменты низших рангов растут и Fi NS 1,Q2 const. В

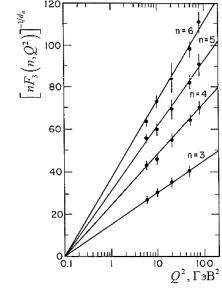
синглетном канале свойством постоянства обладает FiS 2,Q2 . На рис. 1.16 показаны n -е моменты структурной функции F3 x,Q2 ,

полученные экспериментально и вычисленные в рамках пертурбативной КХД. Учитывая поведение константы сильного взаимодействия, определяемое уравнением ренормализационной группы, в логарифмическом масштабе пКХД предсказывает линейный рост моментов структурных функций в соответствующей степени, что и показано на рис. 1.16. Точка пересечения с осью абсцисс определяет значение Q02. Важно отметить, что в случае точного выполнения скейлинга Бьеркена эти прямые должны были быть строго горизонтальными. Наблюдаемое очень хорошее согласие экспериментальных и расчетных данных является существенным свидетельством в пользу справедливости КХД и СМ.

Таким образом, слабое не достаточно быстрое логарифмическое убывание s Q2 с ростом Q2 является причиной нарушения

масштабно-инвариантного поведения структурных функций и приводит в пКХД к слабой зависимости структурных функций и партонных функций распределения от Q2 [19, 20, 22, 35]. Хотя теория является асимптотически свободной, на малых расстояниях все еще имеются некоторые остаточные взаимодействия. Причем изменение моментов как адронных (нуклонных) структурных функций, так и партонных функций распределения определяется уравнения-

68

ми ренормализационной группы и задается аномальными размерностями моментов. Важно отметить, что уравнение ренормализационной группы имеет тесную связь с фракталами и обладает свойством самоподобия, что может приводить к фрактальности и самоподобному поведению структурных функций в пКХД. Более того, уравнения эволюции подразумевают, что возникновение именно фрактальной структуры партонного каскада в импульсном пространстве является предпочтительным, при этом аномальные размерности КХД оказываются тесно связанными с размерностями Реньи. Таким образом, можно ожидать проявления фрактальной структуры партонного каскада и в обычном пространстве-времени.

Рис. 1.16. Момент n -го порядка nF3 n,Q2 в степени 1dn , соответствующий

несинглетной структурной функции xF3 N для глубоко неупругого N -

рассеяния, в зависимости от Q2 . пКХД предсказывает зависимость от lnQ2 (логарифмическое нарушение масштабной инвариантности) [10, 36]

В рамках теории вероятностей также можно получить указание на возможное проявление фрактальности в партонных функциях распределения. Приведенные выше результаты, полученные в рам-

69

ках КХД, допускают следующую вероятностную интерпретацию

явления нарушения скейлинга. Пусть q x		обозначает вероятности
того, что кварк q переносит долю x	импульса нуклона. Увеличе-
ние массы виртуального фотона от t	до t t приводит к увеличе-
нию соответствующей вероятности	от	q x до	q x q x
вследствие того, что другой кварк с долей импульса			x ' x может

испустить глюон и уменьшить тем самым свой импульс от значения x ' до значения x. Таким образом, можно условно считать, что данный кварк содержался в том, который первоначально наблюдался при рассеянии фотона с меньшей виртуальной массой t. Это означает, что распределение кварков в нуклоне является t - зависимым. Можно определить функцию Pqq z , которая соответ-

ствует вариации (на единицу t ) вероятности обнаружения внутри некоторого кварка другого кварка с долей z x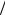 y импульса первоначального кварка, равного y (соответственно, импульс начального кварка рассматривается в долях импульса нуклона). Такая ва-

риация является эффектом порядка

g

2 t ,

где эффективная кон-

станта взаимодействия

g

t

удовлетворяет ренормгрупповому

уравнению [1]. Тогда t -зависимость

q x

(уравнение эволюции)

определяется следующим соотношением:

dq

x,t

1

1

g

2 t dy dz x yz Pqq z q y,t

dt

0

0

g

2 t 1

dy

P

x

q y,t .

0 y

qq

y

Видно, что данное уравнение с точностью до коэффициента совпадает с уравнением DGLAP (1.32) для кварковой несинглетной функции распределения и функция Pqq z может быть отождеств-

лена с функцией расщепления Pqq z . Полученный интеграл имеет

вид свертки, и его можно проанализировать с помощью преобразования Меллина, так как при данном преобразовании, как было указано выше, момент произведения является произведением моментов. Тогда можно получить:

70

dM q		n,t							1	1		dy		x
							g	2	t dxxn 1				Pqq		q y,t
dt												y
									0	0				y
						1					1
			g	2		t dyyn 1q y,t dzzn 1Pqq z										g	2 t M q n,t D n ,
						0					0

где моменты кварковых структурных функций определяются согласно (1.34) и моменты функции, соответствующей вариации вероятности, вводятся следующим образом:

1

D n dzzn 1Pqq z .

0

Таким образом, рассмотрение на основе теории вероятностей нарушения скейлинга приводит к дифференциальному уравнению для моментов кварковых несинглетных функций распределения, решение которого имеет вид

				s t D				n
M q n,t									2b
									.
M	q	n,t0			s t0

Данный результат в точности совпадает с результатом КХД (1.37), полученном при логарифмическом нарушении масштабной инвариантности, если ввести следующее соотношение для аномальных

размерностей и моментов функции Pqq z : 2 qq n, s D n . Как

было отмечено выше, результат КХД получен на основе уравнения ренормализационной группы, которое обладает свойством самоподобия. Таким образом, результат, полученный при вероятностной интерпретации нарушения скейлинга, также указывает на возможный фрактальный характер структурных функций.

Важно напоминать, что фрактальная размерность в классической физике дает некоторую информацию о поведении наблюдаемой (например, длины береговой линии), когда разрешение по длине стремится к нулю. Подобная ситуация возникает и в данном случае, когда рассматриваются адронные структурные функции как

функции Q2 , где величина L 1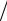Q2 представляет собой длину

волны, определяющую пространственное разрешение (разрешающую способность). В настоящее время в экспериментах по ГНР выполнены исследования в следующих диапазонах кинематиче-

71

ских параметров: 10 6 x 1 и 0,2 Q2 105 ГэВ2 (см. рис. 1.9),

что соответствует L 6 10 4 10 1 фм. Это означает, что в современных экспериментах по ГНР разрешающая способность может достигать 10 3 линейного масштаба нуклона. Отображением про- странственно-временой фрактальной геометрии изучаемого объекта может служить степенное поведение структурных функций в ГНР. В [37] было предложено измерять именно структурные функции в ГНР для определения соответствующих фрактальных размерностей геометрии частиц. Однако модельная зависимость теоретических расчетов и достигнутые экспериментальные возможности не позволили до настоящего времени сделать конкретные выводы, и проблема фрактальной геометрии внутри элементарных частиц остается пока открытой [38]. Таким образом, оказывается, что поведение структурных функций может соответствовать фрак- тало-подобным объектам и важную роль при изучении структуры адрона может играть именно фрактальная геометрия.

Контрольные вопросы

1.Дайте определение процесса глубоко неупругого рассеяния.

2.Приведите систему эволюционных уравнений (DGLAP) для партонных функций распределения.

3.Приведите выражение для эволюции моментов функций распределения в зависимости от переданного импульса.

Рекомендуемая литература

1.1.Андреев И.В. Хромодинамика и жесткие процессы при высоких энергиях. М.: Наука, 1981.

1.2.Roberts R.G. The structure of the proton. Cambridge: Cambridge University Press, 1993.

1.31. Frankfurt L., Strikman M., Weiss Ch. // Annu. Rev. Nucl. Part. Sci. 2005. V.55. P.403.

1 Данный обзор полезен для знакомства с физикой ГНР в области малых значений бьеркеновской переменной, не рассматриваемой в данной главе.

72

Глава 2

НЕДИФФЕРЕНЦИРУЕМЫЕ ИЛИ ФРАКТАЛЬНЫЕ ФУНКЦИИ И МНОЖЕСТВА

§1. Недифференцируемые функции: краткая история возникновения

В своем письме от 15 января 1898 г. к Ф. Клейну Л. Больцман специально отмечал, что «… в природе существуют такие физические проблемы1, для решения которых недифференцируемые функции абсолютно необходимы, и если бы К. Вейерштрасс не придумал бы такие функции, то физикам просто не осталось бы ничего другого, как самим их изобрести…» [39]. Важно отметить, что такие функции и были изобретены. В настоящее время они общеизвестны под названием «обобщенные функции» и широко используются в физике. Применение обобщенных функций для описания случайный процессов во фрактальных средах более подробно рассмотрено ниже (гл. 6).

Существенно и примечательно также то, что одна из основных концепций современного понятия «фрактал» и фрактальной геометрии, а именно, концепция самоподобия вошла в математику с двух независимых направлений (через канторовы множества и функции Вейерштрасса) примерно в одно и то же время для фундаментальных понятий математики: числа и функции (соответственно).

Важно отметить, что еще Г. Лейбниц в своем трактате «Монадология» [40], написанном в 1714 г., использовал понятие самоподобия («миры внутри миров»), а также применял его в определении прямой. Непрерывные функции, не имеющие производных, привлекали внимание многих, в том числе, великих, математиков. В данном параграфе очень кратко описывается история возникновения и развития этой области математики. Более подробно с истори-

1 Здесь имеются в виду проблемы в рамках статистической физики.

73

ческими и методологическими аспектами рассматриваемого направления можно ознакомиться в [41 – 46].

После открытия дифференциального исчисления интуитивно сложилось мнение, что каждую функцию можно дифференцировать любое число раз. В 1806 г. великий французский физик Ампер сделал попытку теоретически обосновать это убеждение на чисто аналитической основе в рамках математической концепции Лагранжа. Позже в разное время одни математики автоматически переносили утверждения Ампера на функции, непрерывные в теперешнем смысле, другие, считая данное утверждение фундаментом всего дифференциального исчисления, приводили свои доказательства этого положения и использовали его в качестве отправной точки для получения других результатов. Среди них были, в частности, Лакруа (1810 г.), Галуа (1831 г.), Раабе (1839 г.), Дюамель

(1847 г.), Ламарье (1855 г.), Фрейсане (1860 г.), Бертран (1864 г.),

Серре и Рубини (1868 г.).

Однако в XIX веке время веры математиков в неразрывность взаимосвязи непрерывности функции и ее дифференцируемости истекло. В 1830 г. Б. Больцано в рукописи «Учение о функции» строит первый пример непрерывной, нигде не дифференцируемой функции. Рукопись данной работы была обнаружена лишь после Первой мировой войны около 1920 г. в Высшей государственной библиотеке [47]. Только через сто лет работа Б. Больцано появилась в печати. В 1834 – 1835 г.г. понятие дифференцируемости и непрерывности четко разграничивает великий русский математик Н.И. Лобачевский. В 1854 г. Дирихле отмечает, что в общем случае нельзя доказать существование производной у произвольной непрерывной функции, и высказывает убеждение в существовании непрерывных функций без производной.

В 1861 г. Риман привел в качестве примера следующую функцию:

	sin n2 x
f x			,	(2.1)
	n	2
n 1

относительно которой Дюбуа-Раймон утверждал, что она не дифференцируема на всюду плотном множестве. К. Вейерштрасс отказался провести доказательство данного факта, и только в 1916 г. Харди, опираясь на некоторые тонкие результаты диофантова ана-

74

лиза, сумел доказать, что рассматриваемая функция f x не име-

ет конечной производной ни в какой точке , где – иррацио-

нальное или рациональное число следующего вида: 2m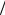4n 1

или 2m 1 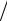2 2n 1 , где m,n – целые. Затем Харди несколько

обобщил пример Римана [48]. В 1969 г. Гервер расширил полученный результат [49] и показал, что функция Римана (2.1) дифференцируема в бесконечном числе точек , где является рацио-

нальным числом с нечетным знаменателем и числителем. В [50] было показано, что других точек дифференцируемости у функции Римана (2.1) нет.

До 1870 г., не считая указанной выше функции Римана (2.1), не было опубликовано ни одного примера непрерывной функции, не имеющей производной на бесконечном множестве точек. Гюэль о таких функциях утверждал, что «… сегодня нет ни одного математика, который поверил бы в существование непрерывных функций без производных…» [51].

В 1870 г. Ханкель [52] предложил метод сгущения особенностей, состоящий в построении функций, у которых нет производных на всюду плотном множестве рациональных точек. Одним из примеров таких функций является функция вида

		1			1
f x				sin n x sin		,
			s
	n 1	n		sin n x

где s – произвольное число такое, что s 1.

В 1873 г. Шварц [53] построил другой пример монотонной непрерывной функции, не имеющей производной на всюду плотном

множестве точек,			2			x
					n
		f x					,
			4	n
		n 1
где x x		, x 0, x
	x x		– целая часть x. Эту функцию

Шварц считал недифференцируемой, но как оказалось позже, она почти всюду имеет конечную производную.

Позже, как принято считать в 1861 г., К. Вейерштрасс построил свою знаменитую функцию [54]:

75

f x W x an cos bn x ,	(2.2)

n 1

где ab 1 3 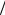2 , 0 a 1, b 1, b – нечетное целое число. К. Вей-

ерштрасс доложил об этом открытии Берлинской академии наук 18 июля 1872 г., однако сам пример недифференцируемой функции (2.2) был опубликован только в 1875 г. Дюбуа-Раймоном [55]. Поэтому как отмечено в [56]: «…год 1875 является не более чем удобной символической датой для обозначения начала Великого кризиса математики…».

Однако появление недифференцируемых функций было воспринято неоднозначно мировым математическим сообществом. Более того, в предисловии к своей книге [57] С. Сакс писал: «…Исследования, имеющие дело с неаналитическими функциями и функциями, нарушающими те законы, которые предполагались всеобщими, эти исследования рассматривались почти как распространение хаоса и анархии там, где предшествующие поколения искали порядка и гармонии…». Ш. Эрмит писал Т. Стильтьесу в 1893 г. «… Я с ужасом и отвращением отворачиваюсь от этой разрастающейся язвы функций, не имеющих производных…» [57]. Даже в начале XX века Дж. Бусенеск был не одинок во мнении, что «весь интерес функции заключается в обладании ею производной» [58], имея в виду обычную производную.

Независимо от К. Вейерштрасса к идее недифференцируемой функции пришел Дарбу, который обобщил примеры Ганкеля и Шварца и построил следующую функцию [59]:

	sin n 1 !x
f x			,	(2.3)
n 1		n!

не имеющую производной при любом значении x. Он доложил о своем результате на заседании Французского математического общества 19 марта 1873 г. и 28 января 1874 г., то есть до выхода в свет публикации Дюбуа-Раймона.

§2. Классы недифференцируемых функций

Исследования, краткая хронология которых приведена выше, послужили основой для построения классов недифференцируемых

76

функций и поиска общих условий дифференцируемости непрерывных функций. Наибольший вклад в данное направление внес итальянский математик У. Дини, вплотную приблизившийся к теореме Лебега о производной непрерывной монотонной функции.

Теорема 2.1. Пусть на отрезке 0,1 задана последовательность

fn x функций, удовлетворяющая следующим условиям:

1. n,n 1,2, : fn x является непрерывной функцией, имею-

щей ограниченную производную на отрезке 0,1 .

2. Ряд fn x сходится на отрезке 0,1 к непрерывной функ-

n 1

ции f x .

3. n,n 1,2, : fn x имеет конечное число экстремумов, при-

чем число их неограниченно возрастает с ростом n и притом так,

что 0	n0	n n0 : расстояние между точками экстремумов
функции fn x		меньше .
4. Если	n	– наибольшее расстояние между двумя последова-

тельными экстремумами, а Dn – наибольшая по абсолютной величине разность двух последовательных экстремальных значений, то

справедливо lim		n	D	0.
n			n
5. Если через	hn		обозначить для каждого значения x те два

приращения (одно из которых положительное, а другое отрицательное), для которых x hn дает первый правый (соответственно,

левый) экстремум, для которого fn x hn fn x Dn 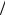2, то можно задать такие положительные числа rn , что для всех x 0,1

и соответствующих каждому из них hn справедливо соотношение

	Rn x hn Rn x		2rn ,	где Rn является остатком ряда fn x
из условия 2.				n 1

77