Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

зависит от двух переменных и возникает нарушение масштабной инвариантности. Данное нарушение слабо зависит от квадрата пе-

реданного импульса lnQ2 , и поэтому обнаруживается на экс-

перименте только при достаточно высоких Q2.

Видно, что в данном случае все сингулярности учитываются в функции распределения (анти)кварка.

Конечная функция h z может быть произвольным образом разделена на две части h z h z h' z . Важно отметить, что

данное разделение зависит от схемы факторизации.

Определение 1.4. Схема факторизации, при которой совместно с сингулярными членами весь дополнительный конечный вклад h z учитывается в функциях распределений (анти)кварков и при

			2	2		2				2
		x,Q					qi x,Q					при
	которой справедливо F2			x ei	qi x,Q

i

отсутствии конечных поправок, например, в следующем за лидирующим порядке (NLO) ТВ КХД O s , называется схемой глу-

боко неупругого рассеяния (ГНР-схемой).

Определение 1.5. Схема факторизации, при которой совместно с сингулярными членами только некоторая (произвольная) часть

дополнительного конечного вклада h z

учитывается в функциях

распределений

(анти)кварков и

при

которой

к формуле

2

2

2

2

F2 x,Q

x ei

qi x,Q

qi x,Q

имеются

конечные по-

i

правки,

например, в NLO ТВ КХД O s , называется схемой ми-

нимальных вычитаний (MS -схемой).

Определение 1.6. Схема факторизации, при которой совместно

с сингулярными членами

только однозначно определенная часть

дополнительного конечного вклада h z

учитывается в функциях

распределений

(анти)кварков и

при

которой

к формуле

2

2

2

2

F2

x,Q

x ei

qi x,Q

qi x,Q

имеются

конечные по-

i

48

правки, например, в NLO ТВ КХД O s , называется схемой мо-

дифицированных минимальных вычитаний (MS -схемой). Количественное определение данной схемы будет приведено

ниже.

В настоящее время ГНР- [29] и MS -схема [30] являются наиболее широко используемыми схемами факторизации.

Для удобства и без потери общности ниже будут рассматриваться только кварковые распределения и соответствующие индексы будут опущены, в качестве схемы факторизации рассматриваются схемы с вычитаниями.

Возможна также другая схема учета сингулярностей в кварковых функциях распределений. Вводится масштаб факторизации 2 так, что расходящийся логарифм в (1.22) может быть записан как

ln Q2		ln Q2	2 ln 2		.
	k02			k02

Сингулярности, связанные с коллинеарным испусканием глюонов учитываются в «голом» кварковом распределении при масштабе факторизации 2 , который играет аналогичную роль, как и масштаб ренормализации. Ренормализованные функции распределения кварков по доли импульса адрона, учитывающие сингуляр-

ность ln 2 k02 и произвольный конечный член h ' z ,

определя-

ются следующим образом [18]:

qi x, 2 qi0 x

s

1

d

x

2

x

qi0

P

ln

2

h

'

(1.25)

2

x

k0

и структурная функция (1.24) запишется как (кварковая часть)

2

2

1

d

2

x

2

2

F2 x,Q

ei

x

qi

,

C

,Q

,

,

(1.26)

где C x ,Q2 , 2

i

x

называются коэффициентными функциями и в

NLO ТВ КХД определяются следующим образом [3]:

2

C z,Q2 , 2 1 z

s

Q

P z ln

h z

2

2

Необходимо отметить, что существует более разумный способ учета инфракрасных и ультрафиолетовых расходимостей – размер-

49

ная регуляризация [18]. Если проводить вычисления не в обычном 4-мерном пространстве, а в 4 -размерном пространстве, где

0, то коллинеарные сингулярности будут проявлять себя как полюса вида 1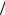 . Данные полюса могут быть включены в определение партонных распределений. Для того чтобы в новом пространстве 4 -измерений константа взаимодействия была также безразмерной, необходимо переопределить безразмерную константу сильного взаимодействия как gs gs R 2. Данное преобразование приводит к возникновению нового масштаба – масштаба ренормализации R , который может быть отождествлен с масштабом

факторизации R .

Тогда формула (1.24) может быть записана

как (кварковая часть)

F2 x,Q2 ei2 x

i

(1.27)

1

d

x

Q

2

2

x

s

qi0 x

qi0 Pqi

ln

hqi

,

2

2

x

где конечная функция

h z

имеет в данном случае следующую

структуру:

h z h z

E

ln 4 P z , E

0,5772... – постоян-

ная Эйлера. Учет следующего однозначно определенного члена2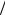 E ln4 в перенормированной функции распределения

q x, 2 количественно определяет схему модифицированного ми-

нимального вычитания (MS -схема).

В рамках данной схемы факторизации справедливо (1.26), где коэффициентные функции определяются следующим образом [18]:

C z,Q2 , 2 CMS

				2
		s		Q
	1 z		P z ln		h z E ln 4 P z
				2
		2

Видно, что представленное выше рассмотрение было ограничено кварк-антикварковыми степенями свободы. Учет глюнных степеней свободы несколько усложняет выражение для структурной

50

функции, приводит к следующей модификации полученного ранее выражения (1.26) [18]:

F2 x,Q2

2	1	d		2		q x
ei	x		qi ,		C
i	x

,Q	2	,	2	g ,	2	C	g x		,Q	2	,	2 (1.28)

и возникновению зависимости структурной функции нуклона от глюонного распределения. Глюонные коэффициентные функции

Cg x ,Q2 , 2 возникают вследствие наличия диаграмм, описы-

вающих g -взаимодействия, и, следовательно, имеют наименьший

порядок s , то есть в отличие от кварковых коэффициентных функций для глюонных функций справедливо:

					2
	Cg z,Q2	, 2	s		Q
				Pg z ln		hg z
					2
			2

Масштабно-зависимые кварковые распределения в данном случае имеют вид [18]:

qi x, 2 qi0 x

s

1

d

x

2

x

qi0

Pqq

ln

2

2

k0

s

1

d

g0

P

x

ln

2

h'

x

2

g

2 x

qg

k0

		x
h'q
				(1.29)

Видно, что коэффициентные функции зависят от схемы факторизации. Поэтому следует быть очень внимательным и использовать согласующиеся коэффициентные функции и функции расщепления. Явный вид коэффициентных функций для NLO ТВ КХД в

рамках MS -схемы приведен в [27].

Вследствие того, что структурные функции являются физически наблюдаемыми и экспериментально измеримыми величинами, они не могут зависеть от нефизического масштабного параметра 2.

Дифференцирование выражения (1.23) по ln 2 приводит к уравнению, определяющему масштабную зависимость кварковых функций распределения [18]:

51

q x, 2				s	1 dy		x
							P		q y, 2	.	(1.30)
ln	2		2		x y
							y

Данное интегродифференциальное уравнение известно как уравнение Альтарелли – Паризи или DGLAP-уравнение [31]1.

При рассмотрении структурных функций в рамках КХД необходимо различать кварковые распределения, которые являются синг-

летами, qiSI x,Q2 , и

несинглетами,

qiNS x,Q2 ,

в

пространстве

ароматов кварков:

qiNS x,Q2 qi x,Q2

qi x,Q2 ,

(1.31)

SI

2

2

2

q

x,Q

qi x,Q

qi x,Q

.

i

Строго говоря, уравнение DGLAP в форме (1.25) справедливо только для несинглетных распределений, в общем случае данное

уравнение является матричным уравнением размерности 2N f 1

в пространстве кварков, антикварков и глюонов [18, 27]:

x

x

t

Pqi qj

, s

Pqi g

, s

j

q

x,t

1

d

q

,t

s

i

,

2

x

x

g ,t

t g x,t

i, j x

Pgqj

, s

Pgg

, s

где t ln Q2 2 . Таким образом, для синглетных, несинглетных

кварковых и глюонной функций распределения можно записать следующую систему эволюционных уравнений:

qiNS x,t

s

t

1

d

x NS

,t ,

P

qi

t

2

x

x

x

(1.32)

x,t

s t

Pqq

, s

2N f Pqg

, s

,t

q

SI

1

q

SI

d

g

x,t

.

2

x

x

t

x

g ,t

, s

Pgg

, s

Pgq

1 Функция расщепления является, соответственно, эволюционным ядром для данного интегродифференциального уравнения.

52

Здесь N f – число кварковых ароматов. Необходимо отметить, что

DGLAP-уравнение (1.31) является аналогом ренормгруппового уравнения для -функции, описывающей эволюцию константы

s 2 , и относится к наиболее важным уравнениям пКХД. Как

было указано выше, для функций расщепления можно записать следующие разложения в виде степенных рядов [27]:

	Pq q z, s ij Pqq0 z			s	Pq 1q z ,
				2
	i j				i j
	Pij z, s Pij 0 z	s	Pij 1 z , ij qg, gq, gg.
		2

В лидирующем порядке ТВ КХД для числа цветов Nc 3 функции расщепления имеют вид:

0			4				1 x2
Pqq										2 1 x ,
		3					1 x
Pqg0			1		x2 1 x 2									,
			2
		4					1 1 x					2
P 0													,										(1.33)
gq			3					x
0				1 x											x	11				N f
Pgg	6							x 1 x												1 x			1 x .
															1 x
							x									12					3
Здесь			«+»-распределение F x																	определяется			таким образом,

что выполняется равенство 1 1 x 1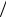 1 x для 0 x 1 и для интеграла от произведения данного распределения и любого доста-

точно гладкого распределения

f x

справедливо следующее ра-

1

1

F x .

венство:

dx

Для NLO ТВ

dxf x F x

f x f 1

0

0

КХД подробное рассмотрение эволюционных уравнений и соответствующие выражения для функций расщепления представлены в

[27].

53

Любая структурная функция может быть преобразована в линейную комбинацию структурных функций ароматового синглета и несинглета (см., например, [8]). Таким образом, представленное выше рассмотрение носит общий характер и применимо для адронных структурных функций любого типа.

3.2.Моменты функций распределений

ианомальные размерности

Для партонных функций распределений оказывается полезным, в том числе при изучении фрактальных свойств (см. ниже), определение моментов.

Определение 1.7. Моментом n -го порядка партонной функции распределения p x,t , p qi qi , g называется функция

1
M p n,t dxxn 1 p x,t ,	(1.34)
0

представляющая собой преобразование Меллина исходной функции распределения.

На основе моментов Mnp t исходное распределение в про-

странстве бьеркеновской переменной x может быть получено с помощью обратного преобразования Меллина:

p x,Q	2		1 c i		n		p	n,t ,
				c i dnx		M
			2 i

где c выбирается таким образом, чтобы контур интегрирования лежал справа относительно всех сингулярностей подынтегрального выражения.

Определение 1.8. Моменты функций расщепления называются аномальными размерностями

			s		1
		n,				dxxn 1P	x,	.	(1.35)
						ij		s
					0

Использование моментов (1.34) и (1.35) позволяет получить альтернативную, более удобную в определенных случаях, формулировку уравнений эволюции. Вследствие того, что преобразование

54

Меллина свертки двух функций1 равно произведению преобразований Меллина данных функций, уравнения эволюции, выраженные в терминах моментов распределений, становятся алгебраическими. Например, в n - пространстве для моментов несинглетной, синглетной кварковой и глюонной функций распределения справедлива следующая система уравнений эволюции:

MiNS n,t				s		t		NS
							qq n, s Mi		n,t ,
					2
		t					t qq n, s		2N f qg n, s MiSI n,t (1.36)
MiSI n,t						s
		M g n,t							gg n, s		.
						2
t								gq n, s			M g n,t

Из второго уравнения системы (1.36) видно, что в общем случае аномальная размерность представляет собой матрицу 2 2, связывающую кварковые и глюонные функции распределения. Однако в тех случаях, когда по квантовым числам участие глюонных партонов невозможно2 аномальная размерность является числовой функцией от s (первое уравнение данной системы). Учитывая соотно-

Q

2

s Q

2

ln

2

2

Q0

КХД

шения t ln

,

,

в простейшем

2КХД

s Q02

2КХД

ln

Q2

случае несинглетных кварковых функций распределения решение уравнения (1.36) имеет следующий вид:

MiNS n,t

s

Q2 dn

qq n, s

, d

.

(1.37)

MiNS n,t0

b

s

Q02

n

Здесь b 11Nc 2N f

3 16 2b, b

– лидирующий

коэффициент

ренормогрупповой -функции.

В лидирующем порядке ТВ КХД аномальные размерности определяются следующим образом (для Nc 3 ) [18]:

1 В данном случае под сверткой двух функций понимается F1 x F2 .

2 Это соответствует несинглетному каналу, зависящему от разности функций распределения кварков и антикварков, например, для функций распределения валентных кварков.

55

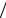
0	4				1				1						n		1
qq	n												2						,
										n n 1
	3				2										k 2 k
0		1					2 n n2									0			4				2 n n2
qg	n													, gq				n									,
	2		n n 1 n 2																	3 n n2				1
0					1				1										1				n	1 N f
gg	n 6																												.
											n n 1				n 1 n 2									k
				12																			k 2			3
																			1						n 1
Необходимо отметить, что вследствие dxxn 2 1																													полюс
																			0

функции расщепления при x 0 проявляется как полюс аномальной размерности при n 1.

Подробно аномальные размерности обсуждаются, например, в [18, 22, 27]. В частности, вычисление значений аномальных размерностей предсказывает, что с ростом Q2 партонные функции распределения логарифмически уменьшаются в области x 0,2, и логарифмически возрастают в области x 0,2. Указанное поведение функций распределений действительно наблюдалось экспериментально (см. ниже).

§4. Некоторые основные экспериментальные результаты

К настоящему времени набран очень значительный объем экспериментальных данных по ГНР. Измерения структурных функций были выполнены в нескольких экспериментах на большой статистике. Более 35 лет исследований привели в результате к достаточно обширным и прецизионным знаниям внутренней структуры нуклона. С тех пор акцент исследований различных аспектов КХД с помощью ГНР стал постепенно смещаться с качественных проверок КХД на точное количественное определение распределений партонов в нуклоне и параметров теории (приложение 1).

Кинематические области доступные для изучения как в ГНР, так и в других процессах при высоких энергиях представлены на рис. 1.9,а, 1.9,б соответственно. Эксперименты на коллайдерах (HERA, Тэватрон) позволили продвинуться в область очень больших Q2.

56

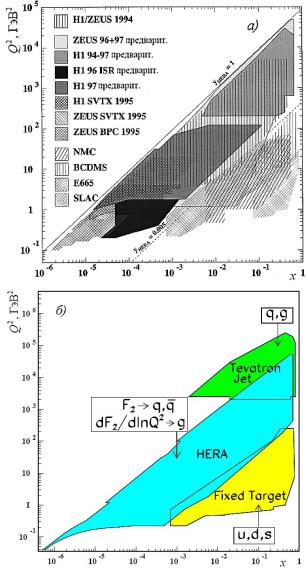
Рис. 1.9. Области в плоскости x,Q2 , где были выполнены измерения структур-

ных функций только в процессах ГНР (а) и совместно с экспериментами по адронным взаимодействиям (б) [24, 28]

57