Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

го произведения – , f 0 – для всех f H0 следует 0; на-

пример, в случае, когда фазовое пространство X ,B является -

компактным метрическим пространством с -алгеброй BX его борелевских подмножеств в качестве B, для выполнения указанного выше условия достаточно чтобы H0 C или даже H0 Cравн. Тогда по резольвенте однозначно восстанавливается переходная функция, а значит, и все конечномерные распределения марковского семейства.

Пользуясь теоремой Фубини и полугрупповым свойством можно получить следующие соотношения:

P hR f x R P h f x e t P t h f x dt			e h e s P s f x ds; (4.7)
0				0
, 0, :R R f x		1		f x R		. (4.8)
			R		f x
В частности, операторы P t ,R ,R	перестановочны.

Определение 4.13. Выражение (4.8) называется резольвентным уравнением; его можно переписать в следующем компактном виде:

R R	R R		1		R		(4.9)
				R		.

Резольвентное уравнение дает возможность установить, что область значений оператора R является одной и той же для всех

0 :R H R H. Вообще говоря, не любую функцию из банахова пространства H можно представить в виде R f x ; но если такое представление возможно, то данная функция представима также в

виде R

x

R

f

x

f

.

Оказывается,

что оператор R , если его рассматривать только

на подпространства H0,

является обратным к оператору I A ,

определенному на DA.

Здесь

I

– тождественный оператор. Иначе

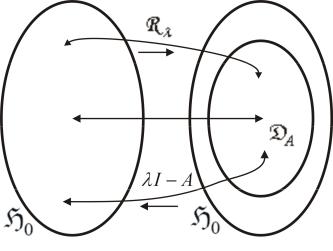
говоря, эти операторы осуществляют обратные по отношению друг к другу взаимно-однозначные отображения H0 на DA и обратно

(рис. 4.1).

178

Рис.4.1. Взаимно-однозначные отображения H0

на DA и обратно

Докажем сформулированное утверждение. Для этого необходи-

мо доказать, что

f x H0 функция

R f x DA

и выполнено

равенство

I A R f x f x ; и что

f x DA будет спра-

ведливо равенство

R I A

f x f

x .

Для

произвольной

функции f x H0

в

силу

определения

4.9

инфинитезимального

оператора

справедлива

следующая

цепочка

соотношений:

f x limh 1

f x R

f x

e t P t f x dt

AR

P hR

lim h 1 e h

h 0

h 0

h

e t P t f

0

x dt .

Вычитая и прибавляя e t P t f x dt, можно

h

получить требуемое равенство AR f x f x R f x . Для произвольной функции f x DA в силу определения 4.9 инфини-

тезимального оператора	справедливы следующие равенства:
		d
R Af x e t P t Af x dt e t			P t f x dt e t P t f x
		dt			0
0	0

179

		f x	d e t	dt f x R f x , что и требовалось дока-
P	t
			dt
0

зать.

Следствие 1. Оператор A однозначно задает полугруппу на подпространстве H0.

Действительно, по известному оператору A находятся операторы I A, 0, по которым находится резольвента, а по найден-

ной резольвенте однозначно восстанавливается полугруппа.

В частности, отсюда следует, что для равномерного стохастически непрерывного марковского семейства на -компактном фазовом пространстве конечномерные распределения однозначно определяются инфинитезимальным оператором A.

Следствие 2. Область определения DA всюду плотна в H0.

Данное утверждение вытекает из того, что DA R H0 и соглас-

но определению 4.9 f H0 существует равномерно сходящаяся к ней последовательность функций R H0.

Следствие 3. Оператор A замкнут1.

Доказательство данного утверждения предоставляется читателю.

Следствие 4. Не может быть двух полугрупп с одним и тем же пространством H0, таких, что инфинитезимальный оператор A

одной из них является расширением инфинитезимального оператора другой.

Ниже без доказательства приводится теорема Хилле – Иосида2. Теорема 4.2 (Хилле – Иосид). Для того, чтобы линейный оператор A с областью определения DA в банаховом пространстве E был инфинитезимальным оператором сильно непрерывной полу-

группы сжимающих операторов P t		(сильная непрерывность озна-
1 Необходимо напомнить, что оператор		A (вообще говоря неотрицатель-

ный) называется замкнутым, если его график – множество пар f , Af –

замкнуто.

2 Подробное доказательство данной теоремы можно найти в [124].

180

чает, что f E P t f f при t 0 ) необходимо и достаточно выполнение следующих условий:

1)DA всюду плотно в E;

2)0 определенный всюду на E оператор I A 1 ;

3) I A 1 1.

В случае полугруппы на подпространстве пространства H ограниченных измеримых функций выполнение условия, что операто-

ры I A 1 сохраняют положительность необходимо и доста-

точно для того, чтобы рассматриваемая полугруппа сохраняла положительность; выполнение условий 1 DA и A1 0 – для того,

чтобы P t1 1.

§3. Диффузионные процессы

Следуя [124], под диффузионным процессом будем понимать (строго говоря) не единичный случайный процесс, а некоторое марковское семейство случайных процессов. Соответственно, более точными и более адекватно отражающими суть были бы тер-

мины «диффузионное семейство» или «семейство диффузионных процессов». Однако первый термин был бы не понятен никому из физиков, знакомых с теорией диффузионных процессов. Термин

«семейство диффузионных процессов» являлся бы хорошим тер-

мином, но только для множества диффузионных процессов, чьи переходные вероятности зависят от некоторого произвольного параметра u :Pu t, x, .

Диффузионные процессы – это, упрощенно, те марковские семейства, инфинитезимальные операторы которых суть дифференциальные операторы; строго говоря, это марковские семейства, траектории которых непрерывны.

Примером диффузионного процесса может служить семейство винеровских процессов, выходящих из всевозможных начальных точек.

Почему выше было указано «упрощенно»? Дело в том, что даже для такого случая, как семейство винеровских процессов в про-

181

странстве Rn n 1 , инфинитезимальный оператор в точности не

совпадает с 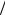2, – оператор Лапласа, так что соотношение между инфинитезимальным и дифференциальным операторами требует дополнительного уточнения. Можно по-разному уточнять (ослаблять / усиливать) требование непрерывности траекторий. Кроме того, в уточнении нуждается и то, требуется ли в определении выполнения какого-либо одного условия (свойства инфинитезимального оператора или непрерывности траектории), или требуется наличие обоих указанных свойств.

Важно отметить, несмотря на то, что свойства инфинитезимального оператора и непрерывности траектории близки друг другу, все же они не совпадают; поэтому можно, варьируя их сочетания, получать близкие друг другу, но все же различные по сути определения. Таким образом, можно констатировать, что единого стандартного определения диффузионного процесса в настоящее время не существует, а есть различные рабочие определения, или, можно сказать по-другому, имеются определения различных классов диффузионных процессов.

Название «диффузионные процессы» объясняется тем, что они являются математическими моделями движения отдельной частицы в процессе диффузии – проникновения одного вещества в другое за счет беспорядочного движения молекул – и в ряде других, схожих с диффузией физических процессов. Известно, что количественная сторона таких процессов хорошо описывается с помощью дифференциальных уравнений с частными производными; с другой стороны, пространственно-временные траектории реальных физических процессов, естественно, непрерывны.

Понятия теории диффузионных процессов оказываются полезными также при изучении явлений совершенно другого порядка реального физического мира, в частности, уравнения диффузионных процессов возникают как предельный случай для дискретных моделей, описывающих различные биологические явления, такие, как, например, изменение с течением времени численности особей определенного биологического вида или концентрации вида в популяции.

Важно отметить, что связь диффузионных процессов с дифференциальными уравнениями двусторонняя. С одной стороны, ре-

182

зультаты из теории дифференциальных уравнений с частными производными можно достаточно успешно применять к описанию диффузионных процессов, с другой – рассмотрение диффузионных процессов позволяет получить некоторые результаты, касающиеся теории дифференциальных уравнений. Одно из применений исследования диффузионных процессов к теории дифференциальных уравнений заключается в приближенном решении уравнений методом Монте–Карло: процесс моделируется при помощи той или иной стохастической процедуры, математические ожидания функционалов от реализации процесса находятся приближенно как среднее арифметическое по большому числу независимых реализаций.

С диффузионными процессами могут быть связаны дифференциальные операторы не выше, чем второго порядка (подробное обоснование данного утверждения приведено ниже). Далее, если специально не оговорено, изложение будет ограничено рассмотре-

нием диффузионных процессов во всем пространстве Rn .

На основе всего вышеизложенного можно дать точное определение диффузионного процесса, используемое в дальнейшем.

Определение 4.14. Марковское семейство t ,Px на фазовом пространстве Rn ,Bn называется диффузионным процессом в

Rn , если оно (семейство) обладает следующими свойствами:

1) его инфинитезимальный оператор L определен на классе

Cфинит2 всех финитных дважды непрерывно дифференцируемых

функций f x и	существуют непрерывные векторная, bi x , и
матричная, aij x ,	функции (причем матрица aij x при любом x

симметрична и неотрицательно определена) такие, что f Cфинит2 1 выполнено следующее соотношение:

1 То есть для любых функций из рассматриваемого класса Cфинит2 ограни-

ченных и равномерно непрерывных вместе со своими частными производными первого и второго порядков функций.

183

	1	n		2	f	x		n	f
Lf x Lf x		aij x						bi x		, (4.10)
					i	j			i
	2 i, j 1		x x					i 1	x

где L – дифференциальный оператор1;

2) все траектории данного семейства непрерывны. Дифференциальный оператор L, определяемый уравнением

(4.10) называется производящим оператором диффузионного процесса2.

Замечание. Возможность удовлетворить условию 2) почти следует из выполнения условия 1).

Действительно, компактифицируя Rn добавлением одной точки, можно получить марковское семейство, удовлетворяющее условиям теоремы 4.2, его (семейства) траектории могут быть выбраны непрерывными. Но непрерывность траекторий в построенном компакте Rn не означает непрерывности траекторий перво-

начального процесса в Rn ; траектория может уйти на бесконечность и прийти из бесконечности. Таким образом, сущность строгого требования непрерывности 2) состоит в запрещении ухода на бесконечность, то есть выхода на границу области, в которой задан процесс.

Как было указано выше, с диффузионными процессами могут быть связаны дифференциальные операторы не выше, чем второго порядка. Можно показать, что если дифференциальный оператор содержит с ненулевым коэффициентом, например, производную третьего порядка f ''', то он не удовлетворяет принципу максиму-

ма: можно найти функцию, имеющую в некоторой точке x0 абсолютный максимум, в то время как значение оператора в этой точке положительно. Следовательно, рассматриваемый дифференциальный оператор может содержать производные лишь первого и вто-

1Уравнение (4.10) подразумевает также, что, как было указано выше, для процесса, называемого диффузионным, инфинитезимальные операторы являются дифференциальными.

2Часто, говоря о виде производящего оператора, указывается результат действия данного оператора на функцию, то есть приводится формула не для L непосредственно, а для Lf . Это соглашение используется ниже.

184

рого порядков1, то есть иметь в одномерном случае следующий вид: a x f '' x b x f ' x 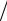2, или в многомерном случае – вид

(4.5)2.

Принцип максимума не позволяет также коэффициентам в (4.10) быть произвольными, а именно в одномерном случае должно быть

x R1 : a x 0; в многомерном случае (как указано в определе-

нии 4.14) – x Rn матрица aij x должна быть неотрицательно

определенной.

Таким образом, дифференциальный оператор, связанный с диффузионным процессом, должен быть эллиптическим оператором второго порядка или вырождающимся эллиптическим оператором того же порядка, то есть оператором, обращающимся в каких-то точках или даже всюду в параболический, или в гиперболический, или даже, вообще, в оператор первого порядка.

Пусть в пространстве Rn заданы непрерывные функции aij x ,

bi x , i, j 1, n и f :	f Cфинит2 – соответствующий им диффе-
ренциальный оператор L,	определяемый в соответствии с (4.10).
Теорема 4.3. Пусть задано марковское семейство t ,Px на фа-

зовом пространстве Rn ,Bn такое, что 0 равномерно по x

выполняются следующие соотношения:

P t, x,V x o t ,								(а)
	yi xi p t, x,dy bi x t				t ,			(б) (4.11)
				o
U x
	yi xi y j x j p t, x,dy aij x t						t ,	(в)
						o
U x

1 Необходимо отметить, что члена вида C x f x не должно быть пото-

му, что инфинитезимальный оператор должен удовлетворять следующему условию: L 0.

2 Появление множителя 12 для одномерного случая обосновывается ниже.

185

i, j 1, n при t 0,U x – -окрестность точки x, а V x – ее

дополнение.

Тогда инфинитезимальный оператор рассматриваемого марковского семейства определен на всех функциях f : f Cфинит2 и на них он равен производящему оператору диффузионного процесса L.

Прежде чем доказывать данную теорему, необходимо прояснить смысл условий (4.11). Первое из них – это достаточное условие для существования марковского семейства с данными переходными вероятностями и с непрерывными траекториями. Достаточно легко доказать, что при справедливости условия (4.11а), если условия (4.11б) и (4.11в) выполнены при каком-нибудь одном положительном , то они выполнены и 0. Выражения в левых частях (4.11б) и (4.11в) – это не что иное, как «урезанные» математические ожидания и ковариации x ti xi и x ti xi tj x j

соответственно1. Условия (4.11б) и (4.11в) означают, что эти вели-

чины имеют первый порядок относительно t	при t 0. Коэффи-
циенты пропорциональности bi x и aij x	поэтому называют

локальными математическими ожиданиями (локальными средни-

ми) и локальными ковариациями (в одномерном случае, а также при i j – локальными дисперсиями) соответственно2.

Приведенные названия связаны с физической интерпретацией диффузионных процессов. Для простейшего случая броуновского движения в однородной изотропной среде, когда на частицу не действуют никакие посторонние силы, кроме ударов молекул, есте-

1 Необходимо отметить, что для получения ковариации нужно еще вычесть произведение математических ожиданий, но им можно пренебречь в

силу того, что оно имеет порядок O t2 o t .

2 Важно отметить, что для рассматриваемых коэффициентов в литературе встречаются и другие названия: для коэффициентов bi x – коэффици-

енты переноса (сноса, дрейфа), или вектор b x называют вектором

переноса; для матрицы aij x – матрица диффузии (в одномерном слу-

чае – коэффициент диффузии).

186

ственно считать коэффициенты диффузии и переноса не зависящими от x и инвариантными относительно вращений, то есть в дан-

ном случае справедливо b x 0, aij x aE, E – единичная

матрица на Rn . Это означает, что такое однородное симметричное броуновское движение является, с точностью до множителя, винеровским процессом.

Доказательство. Пусть взяты f Cфинит2 и 0. Выберем 0 такое, чтобы приращения всех вторых частных производных функции f на отрезках длины, меньшей , были меньше . Для выбранного таким образом 0 выберем h 0 так, чтобы при t h

все o t в условиях (4.11) были по абсолютной величине меньше,

чем t

для всех x Rn. Воспользуемся следующим разложением

Тейлора (здесь x x1, xn , y y1, yn – точки в Rn ):

f y f x

n

f x

yi xi

1

n

2

f x

yi xi y j x j

y x

2 ,

i

i j

i 1

x

2! i, j 1

x y

где

x, y

n2

2 при

y x

. Согласно условию теоре-

мы Rn

U x V x ,

справедлива следующая цепочка равенств:

Pf x P t, x,dy f y

P t, x,dy f y P t, x,dy f y .

Rn

U x

V x

Подставляя в первое слагаемое правой части разложение в ряд

Тейлора, и учитывая, что в пространстве Rn

для выбранной функ-

ции f x Cфинит2

также справедливо интегральное представление

f x P t, x,dy f x

P t, x,dy f x

P t, x,dy f x ,

Rn

U x

V x

можно получить следующее равенство:

f x

Pf x f x

f y f x P t, x,dy

n

yi xi

i

x

V x

U x i 1

187