Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

зики и физики высоких энергий пока ограничено из-за отсутствия их явной физической трактовки. Тем не менее, с возрастанием интереса к процессам множественного рождения частиц, переходным явлениям в рамках КХД, увеличением энергии современных ускорительных комплексов и детектирующих возможностей экспериментальных установок можно ожидать более глубокое использование рассматриваемого математического аппарата в современных исследованиях в области физики фундаментальных взаимодействий.

6.1. Дробные операторы Римана – Лиувилля

Определение 2.13. Операторы I и							I , действующие на функ-
цию x следующим образом:						a	b
Ia x		1		x		t
									dt, x a;
						1
				a		x t
				b			(2.23)
Ib x	1					t
								dt, x b,
						1
				x		t x

называются левосторонним и правосторонним дробным оператором Римана – Лиувилля соответственно.

Справедлива следующая формула дробного интегрирования по частям:

b	b
x Ia x dx x Ib x dx.		(2.24)
a	a

Дробное интегрирование обладает полугрупповым свойством:

	I	I I ;
		a a	a	(2.25)
	Ib Ib Ib
				0, 0 .

Операция дробного дифференцирования вводится естественным образом в качестве операции, обратной дробному интегрированию.

Определение 2.14. Дробные производные Римана – Лиувилля порядка при 0 1 для произвольной функции f x опреде-

ляются следующим образом:

98

Da f x		1		d	x		f t
									dt,
		1 dx a					x t
					b		(2.26)
Db f x		1		d			f t
								dt.
		1 dx
					x		t x

Важно отметить, что если дробные интегралы (2.23) определены для любого порядка 0, то, как было указано выше, дробные производные (2.26) определены только для 0 1. Для более высоких порядков 1 при их целой – , 1 и дробной –

, 0 1

частях числа справедливы следую-

щие определения для дробных производных Римана – Лиувилля:

		1	d n x						f t
Da f x											dt,
									n 1
		n dx					a		x t		(2.27)
		1 n	d n b						f t
Db f x										dt,
									n 1
		n dx					x		t x

где n 1.

Если в приведенных выше формулах – целое число, то под дробной производной порядка понимается обычное дифференцирование:

d Da dx

			d
, Db					,	1,2,3,
			dx

В литературе дробные производные могут обозначаться поразному. Иногда используются следующие обозначения тождественные друг другу:

Da f Ia f Ia 1	f ,
Db f Ib f Ib 1	f , 0.

Пример 2.1.

Рассмотрим функции 1 x x a 1 и 2 x b x 1 , где Re 0. Левосторонний и правосторонний дробный оператор Ри-

99

мана – Лиувилля порядка действуют на эти функции следующим образом:

1

Ia 1

x

x a

,

1

Ib 2

x

b x

.

Дробные интегралы

1 x t

1 b t

a

dt, a x;

x

dt, x b,

x t 1

t x 1

соответствующие лево- и правостороннему дробному оператору Римана – Лиувилля, можно естественным образом расширить с конечного отрезка a,b на полуоси a, или ,b . Для общего

случая x дробные интегралы (т.е. левосторонний и правосторонний дробный операторы Римана – Лиувилля) по всей прямой определяются следующим образом:

I x			1		x	t
							dt;
						1
						x t
						(2.28)
I		x	1			t
					x		dt.
						t x 1

Ряд примеров действия дробных операторов Римана – Лиувилля (2.23) и дробных операторов Римана – Лиувилля на прямой (2.28) для некоторых функций представлены в приложении 2.

Подобно дробным производным Римана – Лиувилля Da и Db

вводятся лиувиллевы производные для всей числовой прямой:

D f x	1		d	x	f		t
									dt,
	1 dx
					x t
					f		t	(2.29)
D f x	1		d						dt,
	1 dx
				x t x

100

где 0 1 и x . Для дробных производных более высоких порядков 1 при n 1 справедливо следующее оп-

ределение для общего случая всей числовой прямой:

		1	d n f x t
D	f x								dt.	(2.30)
							t	1 n
		n dx
						0

Дробные производные Лиувилля на оси D можно привести к более удобному виду, чем (2.29). Получаемые в результате некоторых преобразований конструкции называются дробными производными Маршо:

					f x f x t
D	f x								dt
			1				t1
				0
					x	f x f t
								dt;	(2.31)
		1					1
							x t
					f x f x t
D	f x								dt,
			1				t1
				0

где 0 1 и x .

В теории интегродифференциального исчисления дробных порядков для функций многих переменных, которое1 является дроб-

2

ной степенью оператора Лапласа, широко используется

дробное риссово интегродифференциальное исчисление. В образах Фурье F данная операция записывается в виде:

2			1					I		f , Re 0;
	f	F		x		Ff				(2.32)
							D f , Re 0.

Подробное изложение теории дифференцирования Рисса приведено в [81]. Как следует из теоремы о свертке функций, интеграл

дробного порядка IO f x , Re 0 является сверткой Лапласа следующего вида:

1 Здесь подразумевается исчисление.

101

	1
IO f x f x	x	, Re 0,

вследствие чего имеет место свойство совместного действия преобразования Лапласа и оператора дробного интегрирования.

6.2. Обобщенная формула Лейбница

В случае интегродифференциального исчисления дробных порядков справедливы следующие формулы, представляющие собой обобщения соответствующих формул дифференцирования на произвольные порядки:

g k ,

R1;

Da fg

Da k f

k 0 k

(2.33)

Da k g ,

Da fg

Da k f

k k

где

R1 , , , R1

и

1, 2, 3, при нецелом

.

Обобщенный биномиальный коэффициент определяется как

1

sin

1

.

1 1

1

Замечание. В случае целых значений n

и k обобщен-

ный биномиальный коэффициент переходит в обычный биномиальный коэффициент:

			k	n		n 1		n!
			Cn						.
						k 1 n k 1		k! n k !
				k

В интегродифференциальном исчислении дробных порядков имеет место обобщенная формула Лейбница с остаточным членом:

n 1		Da ku v k Rn ,
Da uv			(2.34)
k 0 k

где остаточный член имеет вид:

	1 n		x	1	x	n 1		n
Rn			x t		u t dt x		v		d .
	n 1 !
			a		t

102

Необходимо отметить, что обобщенная формула Лейбница (1.34) не требует от функции v x бесконечной дифференцируемости.

6.3. Функция Фокса

При интегральных преобразованиях, вводимых для описания диффузионных процессов в средах и пространствах обобщенного типа, в частности, во фрактальных пространствах, и при использовании дробных операторов широко применяется H -функция Фок-

са H mnpq , где 0 m q и 0 n p. Данная функция является функ-

цией общего вида и применяется в физике фундаментальных взаимодействий при изучении корреляционных характеристик процессов множественного образования частиц, в частности, трехчастичных корреляций Бозе – Эйнштейна в случае устойчивых распределений. Функция Фокса представляет собой функцию общего гипергеометрического типа и определяется следующим образом:

a1, 1 , ap

, p

1

mn

s

H pq z

b1, 1 , bq

, q

2 i

C h s z

ds,

m

n

(2.35)

bj j s 1 ai is

h s

j 1

i 1

,

q

p

1 bj j s ai i s

j m 1

i n 1

где i i 0,1, , p , j j 0,1, ,q

являются положительными

числами, ai i 0,1, , p ,bj j 0,1, ,q

– комплексные числа,

удовлетворяющие следующему условию:

k bl

l

ak 1 ,

k 1,2, ,n;l 1,2, m.

Числа и

являются целыми и неотрицательными:

, 0,1,

Контур интегрирования C в комплексной

s -плоскости проходит

так, что полюсы bj

j s j 0,1, ,m

находятся справа, а по-

люсы 1 ai

i s i

1,2, ,n

– слева от контура.

103

Преобразование Лапласа функции Фокса представляет собой также функцию Фокса, но с другими индексами:

	1	n 1,m			1 bj , j
H p		Hq, p 1	p		1,1 , 1 ai , i		,	0 1;
	p
	1	m,n 1			0,1 , ai , i
H p		H p 1,q	p		bj , j	,	1.
	p

Для обратного преобразования Лапласа справедливо:

	H t	1
			Hqn,,pm 1	t
		t

H t 1 H mp ,n1, t

		1 bj , j				0 1;
				,
	1 ai , i , 1,1
			ai , i , 0,1
					,	1.
q t			bj , j

Функция H	является аналитической			функцией при вы-
полнении следующих условий:		0	при	0 и				1 при
q	p	p	q

0, где j i , i i j j .

j 1

i 1

i 1

j 1

Асимптотическое разложение функции Фокса дается формулой

H mp,,qn res h s s ,

справедливой для 0 и n 0 при на каждом замкнутом

секторе arg 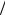2. При этом вычеты должны определяться в

точках s ai 1 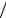i i 1,2, n; 0,1, .

Ниже (гл. 6) более подробно рассмотрено применение функции Фокса для описания процессов во фрактальных средах.

§7. Физическая интерпретация дробных операторов

Различные аспекты применения математического аппарата интегродифференциального исчисления дробных порядков, например, в электромагнетизме обсуждается в [83]. Наличие прямой связи между дробным интегралом и фрактальным множеством Канто-

104

ра подробно рассматривается и доказывается в [84]. Для большей наглядности и более глубокого понимания данной взаимосвязи рассмотрим два предельных случая, широко используемых в физике.

Пусть задана некоторая физическая система, процесс эволюции которой во времени описывается следующим оператором:

t

y t K t, f d .

0

В первом предельном случае функция памяти системы K t,

имеет ступенчатый характер:

t 1,0 t;

K t,

0, t 0.

Тогда в процессе эволюции система будет проходить через все промежуточные состояния непрерывным образом без потерь и справедливо следующее соотношение:

y t	1	t	f d	1 e pt	F p	F p	,
	t			pt
					pt 1	pt
		0

что соответствует полной памяти (эквивалент «прямой»). Здесь

F p	– лапласов образ функции f t .

Во втором предельном случае функция памяти системы представляет собой -функцию:

K t, K t t .

Тогда оператор эволюции системы во времени будет иметь следующий вид:

t

y t t f d f t e pt F p .

0

Данный вид оператора эволюции системы, в свою очередь, означает, что в ходе эволюции система теряет все свои состояния, за исключением единственного с бесконечно большой плотностью (эквивалент «точки» в геометрическом смысле). Этот предельный случай соответствует марковскому процессу без последствия.

Вполне естественно возникает вопрос: существуют ли физические системы, которые в процессе эволюции занимают промежуточное положение между описанными выше предельными случая-

105

ми, то есть между «прямой» и «точкой»? В [84] подробно исследуется данная проблема.

Важно отметить, что классическая геометрия не дает на данный вопрос утвердительного ответа в силу того, что в ней не существует промежуточного геометрического объекта между точкой и прямой. Фрактальная геометрия дает утвердительный ответ на данный вопрос, так как такой объект в рамках фрактальной, неклассической геометрии существует и называется канторовым множеством. Ввиду важности опишем более подробно промежуточный случай эволюции физической системы и ее взаимосвязь с соответствующим объектом фрактальной геометрии.

При рассмотрении взаимосвязи между дробным интегралом и фрактальным множеством Кантора используется ступенчатая функция следующего вида:

	1	,t	2		;
1, если t
t1 t2				.
0, если t1,t2

Пусть длина временного интервала, в течение которого исследуется эволюция физической системы, составляет t. Данный интервал делится на три равные части. После удаления средней части интервала остаются два концевых временных отрезка, длина каждого из которых равна t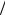 13 1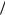2 . Затем процедура повторя-

ется. Подробно алгоритм построения канторова совершенного

множества описан в [78]. Конечный вклад в интеграл от 2N временных отрезков на N -м этапе разбиения записывается в виде:

	1			t 2N			N		N
y t					t			t			f d
		N					m		m 1
	2		t
				0 m 1

с соответствующим преобразованием Лапласа

p

1 exp pt N

Q pt

1

F

p

.

N

pt

n

Здесь функция Qn x определяется следующим образом:

Qn 2		N 1				pt 1 .
	N		n				(2.36)
		1 exp			,

n 0

106

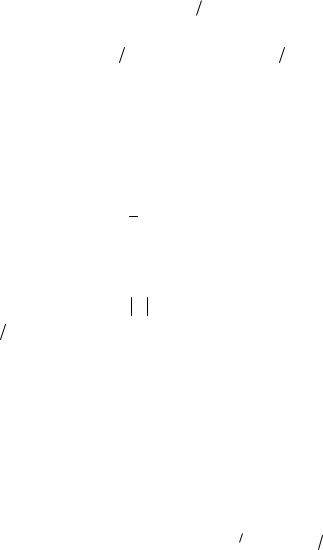
Функция Qn , определяемая выражением (2.36), удовлетворяет функциональному уравнению

Q

1 exp

Q

N 1

,

(2.37)

n

2

которое при условиях

1

pt

N и

0

t 1 принимает

следующий вид:

Q

1

Q

.

N 1

n

2

Переходя к пределу при N ,

можно получить уравнение

1

Q

Q

2

с решением

Q A ,

где DF ln2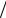ln 1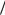 – фрактальная (хаусдорфова) размерность

канторова множества [78].

Таким образом, в [84] было показано, что в промежуточной области значений величины pt , которая определяется неравенства-

ми	1	pt	N , функция p	принимает следующий
вид:			p A 1 pt	F p .
					(2.38)

В свою очередь, соотношению (2.38) соответствует представление y t в виде дробного интеграла:

1

t

y

t

A

t 1

t 1 f d

0

(2.39)

A

1

1

1 u

f ut du,

1

0

где 0 1, 0 t;

коэффициент

A

2

2. Для 1 2 показа-

тель имеет целочисленное значение, при этом фрактальная раз-

107