Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

является стандартным винеровским процессом [134, 136]. В частности, отсюда следует, что реализации процесса Орнштейна – Уленбека непрерывны и нигде недифференцируемы почти наверное и что почти наверное справедливо [134]

v t v 0

v t

lim

1, lim

1.

t 0 4 2t ln ln 1 t

t 0

2 2 ln t

Многомерный процесс Орштейна – Уленбека vt vt 1 , ,vt n

может быть определен как решение соответствующего многомерного уравнения Ланжевена [135]:

dvt Bvtdt Adwt ,

где wt wt 1 , ,wt n , wt i – стохастически независимые стацио-

нарные винеровские процессы с корреляционной функцией, опре-

деляемой как i

k t,s

ik

min t,s . Здесь

B b

ik

и A a

ik

суть n n

wt

ws

матрицы, причем матрица a ik связана с диффузион-

ной матрицей a ik ,

входящей в уравнение Фоккера – Планка со-

отношением a ik aaT

ik .

Уравнение Фоккера – Планка для мно-

гомерного процесса Орштейна – Уленбека имеет вид

p t, x, y

1

n 2

aij

y p t, x, y

n bik y yk p t, x, y

,

t

y

i

y

j

y

i

2 i, j 1

i 1

фундаментальное решение которого есть

p t, x, y 2 n 2

det 1 2 exp yi

1 ik yk ,

где

t

e B t

e B t

y y

e Bt

x

k

,

d

.

i

i

ik

ik

ij

jl

lk

0

Пример 5.1.

Простейшим примером двумерного n 2 процесса Орштейна

– Уленбека может служить гармонический стохастический процесс xt , описываемый стохастическим дифференциальным уравнением dxt 2 dxt 02 xtdt dwt ,

238

где wt – стандартный винеровский процесс, 0 – частота свободных колебаний, – коэффициент затухания, – интенсивность внешнего шума. Уравнение Ланжевена для стохастического гармо-

нического процесса

в терминах

двухкомпонентных векторов

Ut

xt

и dWt

0

приобретает вид

x

t

dw

0

t

0

0

dU

t

BU

dt dW ,

B

.

t

t

0

2

Корреляционная

функция

двумерного

процесса

Wt имеет вид:

i

k

t,s ik

min t,s ,

где матрица

0

0

[135].

0

0

1

Wt Ws

§9. Обобщенное (фрактальное) броуновское движение

Понятие обобщенного (фрактального) броуновского движения

– ФБД – BH t было введено Б. Мандельбротом [56, 137] с помо-

щью замены показателя в формулах для математического ожидания и дисперсии приращений классического броуновского движе-

ния на	произвольное	действительное число H 0,1 . Случай
H 1 2	соответствует	независимым приращениям и описывает

классическое броуновское движение. Таким образом, ФБД оказалось удобно определять именно с помощью параметра H. Показатель H , в силу исторических причин, называется показателем Херста. Существование фрактального броуновского движения было доказано в [129] с использованием стохастических интегралов. Как будет показано ниже, реализация одномерного ФБД с параметром H имеет размерность d 2 H. Графическим образом двумерного ФБД является поверхность, имеющая размерность d 3 H. Таким образом, параметр H соответствует степени изрезанности графического образа обобщенного (фрактального) броуновского движения. Как и в случае классического броуновского движения,

239

будет дано определение ФБД, основанное на нескольких аксиомах, которые характеризуют случайный процесс этого типа.

9.1. Определение ФБД

Определение 5.6. Гауссовский процесс BH t называется обоб-

щенным (фрактальным) броуновским движением с параметром H , H 0,1 на отрезке a,b , если он обладает следующими свой-

ствами:

1) BH 0 0 и функция BH t почти всюду непрерывна на от-

резке a,b ;

2) (свойство гауссовости приращений) t2 t1 случайная вели-

чина BH BH t2 BH t1 имеет гауссово (нормальное) распреде-

ление с нулевым математическим ожиданием и дисперсией равной

2 t2 t1 2H , где – положительная константа, то есть

P BH x

1

x

u2

exp

du.

2

2

t

t

2 H

2

2H

2

t2

t1

2

1

Как было указано выше, процесс ФБД является частным случаем автомодельного случайного процесса.

9.2. Основные свойства ФБД

Закон дисперсии и стационарность. Из свойства 2) определения ФБД следует соответствующий закон дисперсии:

t1,t2 a,b : D BH t2 BH t1 2 t2 t1 2H .

Вданном случае наблюдается полная аналогия с классическим броуновским движением: в силу того, что дисперсия зависит толь-

ко от модуля разности значений моментов времени t2 и t1, но не от самих значений, то приращения в случае ФБД являются стационарными.

Свойство зависимости приращений. В отличие от классическо-

го броуновского движения B t , приращения которого независи-

240

мы, ФБД BH t с параметром H 1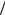2 не обладает данным свойст-

вом.

Теорема 5.12. Пусть BH t – обобщенное (фрактальное) бро-

уновское движение с параметром H , H 0,1 . Приращения BH t

независимы тогда и только тогда, когда H 1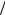2.

Доказательство. t 0, t 0 рассмотрим следующие прира-

H

B

H

0

и

H

t

t

B

H

t

По свойству 1)

щения: B

t

B

.

определения ФБД BH 0

0, поэтому справедливо равенство

H

t

H

0

H

t t

H

B

B

B

B t

(5.16)

H

t

H

t t

H

t

B

B

B

.

С другой стороны, справедливо следующее соотношение:

B

H

t t

B

H

0

2

B

t

B

H

0

2

H

(5.17)

B

H

t t

B

t

2

2B

t

B

H

t t

B

t

H

H

.

H

Докажем необходимость.

Пусть приращения ФБД

BH t неза-

висимы, тогда нужно доказать, что H 1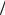2. В силу свойства 2) оп-

ределения ФБД приращения BH t имеют гауссовское распреде-

ление с математическим ожиданием равным нулю, поэтому независимость приращений приводит к следующим равенствам:

BH t BH 0 BH t t BH t

BH t BH 0 BH t t BH t 0.

Сдругой стороны, в силу закона дисперсии и равенств (5.16) и

(5.17) должна выполняться цепочка следующих соотношений:

BH t BH 0 BH t t BH t 2 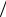2 t t 2H t2H

t 2H 0, что возможно только при выполнении условия

H 1 2.

Действительно, при

H 1 2 1 2H 0

и справедливо

2

t t 2H t2H t 2H

2

t

t

t

t t 1 2H

t t 1 2H

t1 2H

2

2

241

	t		2			1
				t
	t 1 2H					t t 1 2H
			2

		1			1
				t
					1 2H
	t	1 2H
					t t

1

1 2H

t

0.

При

H 1 2 1 2H 0

и

справедливо

неравенство

2

2H 1

t

2H 1

t t t

2H 1

t

2H 1

2

t t t

0.

Необхо-

димость доказана.

H 1 2,

Докажем

достаточность. Пусть

значение параметра

тогда нужно доказать, что ФБД BH t

имеет независимые прира-

щения. Из соотношений (5.16) и (5.17) следует, что t

0, t 0:

B

t B

0 B

t t B

t

1

B

t t

B

0 2

H

H

H

H

2

H

H

B

H

t B

0

2

B

H

t t

B

t

2

.

Отсюда, используя за-

H

H

кон дисперсии для ФБД и учитывая H 1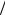2, можно получить ра-

венства BH t BH 0 BH t t BH t 12 t t 2 H

t2H t 2H 0. В силу свойства 2) – равенство нулю математи-

ческих

ожиданий приращений ФБД –

H

t

B

H

0

и

B

0

H

t

t

B

H

t

0. Таким образом, при

H 1 2 выполнено

B

равенство,

указывающее

на

независимость

приращений:

B

t

B

0

B

t t

B

H

t

B

H

t

B

H

0

H

H

H

BH t t BH t . Достаточность доказана. Теорема доказа-

на. ▲ Немарковское свойство. Из вычислений, выполненных при до-

казательстве теоремы 5.12, можно получить важные следствия. Если H 1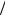2, то BH t BH 0 и BH t t BH t имеют, ско-

рее всего, одинаковые знаки и функция BH t обычно возрастает в будущем, если она возрастала в прошлом. Если H 1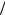2, то прира-

щения

H

t

B

H

0

и

H

t t

H

t

имеют, скорее все-

B

B

B

242

го, различные знаки и функция BH t обычно убывает в будущем,

если она возрастала в прошлом. В совокупности данные факты говорят о том, что ФБД не является марковским процессом, за исключением частного случая H 1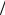2.

Обобщенный (фрактальный) броуновский процесс имеет дисперсию приращений, определяемую по следующей формуле:

D B

t

B

t

K

t2

t1

2H

t

t

2 H .

(5.18)

2

H

2

H

1

P

1

Важно отметить, что обобщенное (фрактальное) броуновское движение имеет бесконечно большое время корреляции. Согласно определению ФБД BH 0 0 и пусть 1, KP 1. Тогда из фор-

мулы (5.18) получается следующее выражение для коэффициента корреляции:

r t	D BH t BH t	2	2H 1	1.	(5.19)
	DBH2 t

Можно заметить, что при H 1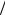2 корреляции прошлых и будущих приращений отсутствуют в любой момент времени: t : r t 0 и

коэффициент корреляции не зависит от t в соответствии с (5.19). Случай H 12 соответствует наличию положительной корреля-

ции, случай H 1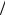2 – отрицательной корреляции.

Таким образом, уникальное свойство обобщенного броуновского процесса заключается в наличии явления персистентности – сохранения имеющейся тенденции (при H 1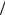2 ) и антиперсистент-

ности – изменения имеющейся тенденции (при H 1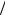2 ). Ввиду важности поясним суть данного явления более подробно. Если приращения были положительными за некоторый промежуток времени в прошлом и H 1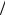2, то есть имеет место поддержание имеющейся тенденции, то и в будущем в среднем приращения будут положительными. Более того, данное утверждение справедливо для произвольно больших t. В противоположном случае, для H 1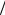2, рост в прошлом означает уменьшение в будущем, и наоборот. Следовательно, суть обобщения состоит в том, что обобщенный броуновский процесс (в отличие от классического) обладает памятью.

243

Абсолютная величина приращений. Пусть BH t – ФБД с пара-

метром H , H 0,1 . Тогда математическое ожидание абсолютной величины приращения равно:

M

BH t2

BH t1

2

t2 t1

H

.

Доказательство данного факта полностью аналогично доказательству теоремы 5.1 и предоставляется читателю.

Недифференцируемость. Как и в случае классического броуновского движения, ФБД почти наверное недифференцируемо. Полное доказательство данного утверждения приведено в [129].

Сравнение результатов численного моделирования для поведения приращений броуновской функции и собственно самой функции в случае классического и обобщенного (фрактального) броуновского движения представлено ниже (см. §11, рис.5.7).

§10. Некоторые важные примеры процессов обобщенного броуновского движения

Иная, полезная для различных приложений, формулировка свойства памяти для обобщенного броуновского процесса приведена, например, в [129]. Стимулом проведения исследований в [129] была необходимость понимания разности потоков крови в сердце и легких. Ранее было обнаружено, что местные потоки крови в органах человека обладают свойством фрактальности. Для местных сердечных потоков крови фрактальная размерность DF 0,5 1 при коэффициенте корреляции, равном 0,52. Здесь статистика Херста есть результат длинного потока взаимосвязанных событий. В данном случае присутствует не кратковременная память, которую называют «марковской», а долговременная. Фрактальная природа показателя Херста H определяет меру смещения событий. Тестом для проверки фрактальности потоков крови явля-

1 В данной главе, в отличие от [1], для обозначения фрактальной размерности используется DF для того, чтобы не путать с обозначением дисперсии, например, в (5.19).

244

лись выражения для корреляций между искусственными сериями моделирующих сигналов, разделенных интервалами.

Рассмотрение корреляций сумм значений сигналов на двух интервалах, разнесенных на n смежных единичных отрезков, позволяет получить следующее общее выражение для значений коэффициентов корреляции rn :

		n 1					n 1
rn					n 1 2H 1 1		n i 1 ri
				2			i 1	(5.20)
			1
				n 1 2H		2n2H n 1 2H .
			2

Отсюда, в частности, можно получить формулу (5.19) для простейшего случая n 1, r2 1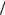2 32H 1 22H , и т.д.

Для одномерных сигналов показатель Херста связан с фрактальной размерностью простой формулой H 2 DF . В общем случае, между евклидовой или топологической размерностью dim M , показателем Херста и фрактальной размерностью имеет место следующее соотношение [137]:

H dim M 1 DF .

Значения коэффициента корреляции rn сигналов, разделенных

n 1 целыми интервалами для некоторых фиксированных значе-

ний показателя H , представлены на рис. 5.5. Видно, что при увеличении числа интервалов n корреляции сначала быстро ослабевают (соответствующие коэффициенты уменьшаются), затем, при больших n, уменьшение rn происходит значительно медленнее.

Для фрактальных сигналов с H 0,7 значения rn при n 1 настолько малы, что можно рассматривать данные сигналы как фрактальные шумы. Из формулы (5.20) следует, что для абсолютно случайных фрактальных потоков r1 0 значение фрактальной раз-

мерности равно DF 1,5 и H 0,5. На основании (5.20) может быть получено следующее асимптотическое соотношение:

rn

rn 1

	n			2H 2
				.
n 1

245

x 1.

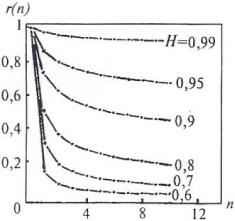
Рис.5.5. Коэффициенты корреляции при различных значениях показателя Херста. Точки соединены для наглядности [78]

Используя аналогичный подход можно получить следующее соотношение для непрерывного случая:

r x

1

x 1

2H 2

x

2H

x 1

2H ,

(5.21)

2

где x 0 – непрерывная переменная.

Важно отметить, что корреляционные кривые (5.21) непрерывны без разрывов производной, кроме выделенного случая H 0,5, когда коэффициент корреляции задается следующей формулой:

1 x, 0 x 1; r x

0,

Вид зависимостей rn (см. рис. 5.5) также интересен тем, что они предсказывают ослабление корреляций, однако более медленное, чем для экспоненциальных или гауссовых кривых. Ослабление корреляций (уменьшение rn ) описывается почти степенной функцией с показателем n, тогда как экспоненциальная и гауссова зависимости спадают более резко.

Для определения показателя Херста по формуле (5.20), например, в [129] генерировался фрактальный сигнал из 32768 равномерно расположенных точек. Оценка проводилась выполнением обратного преобразования Фурье в частотной области спектра

246

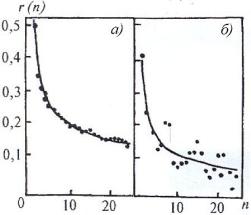
1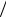 f 2H при значении H 0,8 и случайной фазе, где f – частота. Было получено следующее значение: H 0,800 0.003. При фрактальном сигнале из 512 точек показатель Херста был оценен равным H 0,74 0,02. Двухточечные автокорреляционные функции для сигнала с разными отсчетами представлены на рис. 5.6,а и 5.6,б соответственно.

Из приведенных выше рассуждений следует, что возможна ситуация, при которой за ограниченное время измерения вообще невозможно получить достоверные данные о среднем изучаемого процесса. Следовательно, нахождение показателя Херста является необходимым элементом измерения статистических свойств исследуемых процессов [56].

§11. Моделирование обобщенного броуновского движения

Для более глубокого понимания обобщенного броуновского движения и его реализации методами численного моделирования рассмотрим подробно предложенные последовательно варианты определения функции BH t . В [138] была введена случайная

функция BH t с нулевым средним:

Рис.5.6. Проверка соответствия модели для фрактальной корреляции синтезированного фрактального сигнала с показателем Херста H 0,8: а – рассматривается массив из 32768 точек, б – рассматривается массив из 512 точек [78]

247