Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

R t c 2t log logt .

доказать не удалось бы. При попытках провести такое доказательство мы столкнулись бы с большими колебаниями и частот, и средних, поскольку при реализации большого значения величина

t продолжает оставаться большой в течение большого интерва-

ла на логарифмической шкале.

Закон повторного логарифма1 для больших значений R t име-

ет ту же форму, что и для значений каждой компоненты случайно-

го вектора OA t . Таким образом, имеет место следующая теорема.

Теорема 5.3. Если c 1, то почти наверное, что неравенство

R t c2t log logt (5.7)

выполняется для всех достаточно больших t. Наоборот, если c 1, то почти наверное найдутся сколь угодно большие t, при которых реализуется неравенство, противоположное (5.7):

(5.8)

Доказательство. Пусть c 0. Назовем событием A ситуацию, когда неравенство (5.7) оказывается несправедливым при хотя бы некоторых произвольно больших t, а событием B назовем ситуацию, когда для произвольно больших t одновременно выполняются следующие соотношения:

	R t c		,	1	2		2	,
		2t log logt
					n
							n

где – угол между вектором OA и осью Ox1, меняющийся от нуля до 2 , n – некоторое сколь угодно большое целое число. Если событие A осуществилось, то осуществляется хотя бы одно из со-

бытий B . Поскольку, в силу изотропии процесса, все события B

имеют одинаковую вероятность, величина P B положительна,

если положительна величина P A . Таким образом, для сколь

угодно больших значений t с положительной вероятностью справедливы следующие соотношения:

1 Формулировка и доказательство теоремы Хинчина (закона повторного логарифма) приведены в приложении 5.

218

		t R t cos	2			,	c' c cos	2	.
	X1			c'	2t log logt					(5.9)
			n					n
	Если c 1,	то можно выбрать настолько большое число n,								что бу-

дет также справедливо c ' 1 и неравенство (5.9) придет в противоречие с теоремой Хинчина1. Итак, если c 1, то P A 0.

Пусть теперь c 1. Часть теоремы, соответствующая данному случаю, справедлива в силу того, что всякая нижняя грань функции

X1 t является нижней гранью R t и сформулированное свойст-

во следует непосредственно из теоремы Хинчина. Теорема доказана. ▲

Итак, по крайне мере в приближении теоремы Хинчина большие значения R t не превосходят больших значений X1 t , хотя и

появляются чаще, так что в данном случае на бесконечности график частот стремится к нулю не столь быстро.

4.2. Полярный угол: дискретный	случай
Обозначим через n An 1OAn ,	изменяющийся от	до
(поскольку вероятность значений	равна нулю, не имеет значе-

ния, какое именно из этих значений указывать:							или ), и по-
		n
ложим n		i .		Тогда n – один из полярных углов точки An .
		i 1		A q		является концом вектора
Точка An		A tn			n
								An 1 An n
			, где n – приведенный вектор,
	qn 1 q 1						распределенный по

нормальному закону и не зависящий от OAn 1. Отсюда следует, что форма OAn 1 An , а следовательно, и значения угла n распределе-

ны по закону, зависящему от n 1 как от параметра. Поскольку раз-

личные величины параметра n 1 имеют частоты, почти наверное стремящиеся к своим теоретическим вероятностям, определяемым согласно (5.5), то для значений угла n в среднем справедлив неко-

1 Подробнее о теореме Хинчина – см. приложение 5.

219

торый априорный вполне определенный стационарный закон рас-

пределения, для которого M n 0, M n2 2 , 0, . Сле-

довательно,

n n n,

(5.10)

где величина n распределена по закону, стремящемуся к приведенному нормальному закону при n .

Более того, в некотором смысле приращения величины полярного угла n можно сравнить с выигрышем при игре в «орла и решку». Однако в данном случае различные возможные значенияn осуществляются последовательно в тех же условиях, что и воз-

можные значения величины n , а применение закона повторного логарифма показывает, что величина угла n колеблется между большими по модулю значениями 1 2n log logn , где –

величина, стремящаяся к нулю при n . Как очень большие положительные, так и очень большие отрицательные значения редки и n , как правило, конечна.

Данные рассуждения приводят к мысли, что ломаная A0 A1 An почти наверное обходит точку O весьма нерегулярным образом.

4.3. Полярный угол: непрерывный случай
Обозначим t полярный угол точки	A t , отсчитывае-
мый от направления, определяемого вектором	OA0. Данный угол

меняется непрерывно при t 0, кроме случая возврата кривой C в точку O. Необходимо отметить, что в дальнейшем будет показано, что кривая C есть множество, имеющее плоскую меру нуль: вероятность того, что она проходит через заданную точку, равна нулю. Следовательно, возможностью возврата рассматриваемой кривой в точку O можно пренебречь.

Определим угол n следующим образом:

n tn tn 1 .

220

Определенный таким образом угол отличается от соответствующего угла n на число, кратное 2 , которое, очевидно, может быть не равно нулю – замкнутый контур, составленный из дуги An 1 An и ее хорды, действительно может окружать начало O. Важно отметить, что любая дуга непрерывной кривой имеет положительную вероятность приближать, с любой заданной точностью , дугу

An 1 An . Таким образом,	если точка		A tn 1	известна, то справедли-
во соотношение P n	n 2 h		A tn 1	A tn h n 1 0 и

при n каждое событие n n 2 h h 0, 1, 2, осуществляется с частотой, почти наверное стремящейся к априорной положительной вероятности с математическим ожиданием

n n 1 .

Величина n2 бесконечна, откуда следует, что ожидаемый по-

рядок величины t превышает порядок величины t. Согласно

[130], отметим кратко, что доказательство данного утверждения основано на том факте, что справедливо следующее равенство:

			2					d
		1	OA0		exp 2		2		.
						0
		Если q 1				мало, то угол 1			A0OA1 или не мал, или не одно-

го порядка со своим тангенсом, который определяется следующим

образом: tg

q 1

,OH

OA

где

и – незави-

1

0

q 1,

OH

0

0

симые друг от друга переменные, распределенные по приведенно-

му нормальному закону, OH0 OH0 . Математическое ожидание

2 2

величин 1 OH0 и 1 OA0 равны бесконечности, откуда следу-

ет, что математическое ожидание величины 2 , очевидно, конечно и велико по отношению к q 1 log q при q 1 0.

Пусть t0 1 и некоторое t – заданы. Положим t qn . В случае,

если n неограниченно возрастает и q 1, угол 1 представляется

221

суммой n углов , не зависимых друг от друга, причем 2

будет велико по отношению к log q logt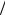n. Поэтому средний квадрат данной суммы растет неограниченно вместе с n, то есть математическое ожидание квадрата полярного угла t равно:

2 t .

4.4. Характер кривой C в окрестности заданной точки

На первом этапе рассмотрим окрестность точки O A 0 . Опи-

раясь на локальное свойство винеровской функции X t , можно

утверждать, что в плоском случае справедлива следующая теорема. Теорема 5.4. Стохастические свойства приведенной случайной

вектор-функции OA t 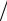t инвариантны относительно замены t на

обратную величину t 1.

Как следствие можно получить, что вероятный ход кривой C в окрестности начала выводится из результатов, описывающих ее поведение на бесконечности1. Важно отметить, что предыдущие рассуждения столь же хорошо выполняются и для величин tn , образующих бесконечно убывающую геометрическую прогрессию.

Таким образом, все, что было выше сказано относительно поведения полярного угла t без изменений справедливо для случая,

когда t 0. Точка A t стремится к точке O, только вращаясь во-

круг нее то в одном, то в другом направлении, так что угол t не ограничен ни снизу, ни сверху.

Этот результат описывает также характер подхода точки A t к

некоторой точке A t0 при t t0 (либо слева, либо справа), если только на t0 априрори не налагается особого условия, как напри-

1 Подразумеваются начальный и бесконечно удаленный моменты времени, в силу того, что параметр t в физическом смысле отождествляется со временем.

222

мер, требования быть точкой, в которой одна из координат достигает (локально) наименьшего или наибольшего значения.

Исключительно важно отметить, что данное замечание показывает крайнюю сложность броуновской кривой C, в силу которой невозможно представить все бесконечно малые детали ее хода. Уже один только факт, что любая дуга кривой C имеет бесконечную длину, позволяет предвидеть эту сложность.

Можно поставить вопрос о существовании у каждой дуги кривой C бесконечного множества двойных точек1. В [130] было указано, что «…применение точного математического закона может сделать то, чего не может сделать случайность…». Для того чтобы не было двойных точек, необходимо чтобы точка A t , постоянно

перемещаясь в окрестности своих прежних следов, никогда бы их не пересекала. Полностью случайный механизм без наличия эффекта памяти такого поведения обеспечить не может.

Ввиду важности рассмотрим данный момент более подробно и строго. Любая дуга произвольной непрерывной кривой имеет по-

ложительную вероятность		быть приближением случайной дуги
A t A t ' . Следовательно,		вероятность существования двойной
точки у дуги A t A t '	положительна и не зависит от соответст-
вующей разности t ' t ,	поскольку процесс не изменяется при за-

мене t 2t h и OA OA, где ,h – некоторые величины. Рас-

смотрим теперь растущую последовательность значений n вели-

чины t, имеющую конечный предел lim n t. Различные дуги

n

A n A n 1 имеют независимые друг от друга формы. Но тогда

согласно лемме Бореля следует, что почти наверное у бесконечно большого числа этих дуг имеются двойные точки. Таким образом, почти наверное существует бесконечное множество двойных точек

1 Под двойной точкой подразумевается точка, в которой кривая пересекает саму себя один раз, то есть кривая проходит через двойную точку дважды.

223

на дуге A 1 A t ' , а следовательно, и на произвольной дуге

A t A t ' .

§5. Некоторые основные теоремы для кривой плоского броуновского движения

В данном параграфе приводится строгое обоснование описанного выше возможного строения кривой плоского броуновского движения C.

Теорема 5.5. Пусть L – произвольная конечная непрерывная кривая и AB – дуга данной кривой. Тогда AB рассматриваемой

кривой L и 0 вероятность события «броуновская точка A t ,

выходящая из A, в заданный момент времени подойдет к точке B на расстояние, меньше , двигаясь все это время в - окрестности дуги AB » строго положительна.

Доказательство. Возьмем произвольное 0 и зафиксируем его. Определим ломаную A0 A1 An , A0 A, описываемую точкой, расстояние от которой до точки, описывающей дугу AB, не будет превышать 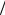2, то есть определим ломаную A0 A1 An в 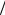2 - окрестности дуги AB (рис. 5.2). Для доказательства теоремы достаточно доказать, что броуновская точка A t с точностью до 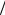2

может описать определенную выше линию A0 A1 An , другими словами, поскольку замена на 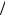2 ничего не меняет, сформулированную теорему достаточно доказать в случае ломаной.

Обозначим через	p , p 1,2, ,n вероятность		того, что бро-
уновская точка A t ,	выходящая из точки Ap 1,	описывает отрезок
Ap 1 Ap выбранной ломаной с точностью до		n,	то есть в своем

движении удаляясь от данного отрезка менее, чем на 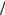n, подхо-

дит к точке Ap ближе, чем на 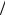n. Тогда, согласно трансляцион-

ной инвариантности броуновского движения, вероятность того, что броуновская точка A t , в конце концов попадающая из начальной

224

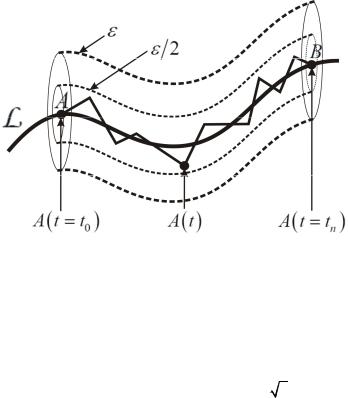
точки A0 A в окрестность точки Ap , проходит свой путь, не от-

клоняясь от выбранной ломаной более, чем на , равна, по мень-

p

шей мере, i , p 1,2, ,n. Следовательно, достаточно доказать

i 1

положительность всех p , p 1,2, ,n, то есть, что сформулиро-

ванная теорема верна в случае отрезка прямой AB длины l.

Рис.5.2. Рассматриваемые в рамках доказательства теоремы 5.5 окрестности выбранной дуги непрерывной кривой

Примем точку A за начало координат, а AB за ось

x1. Тогда

координаты X1 0 X2 0 0. Если при заданном T

будет вы-

полнено неравенство

X1 T l

и при всех

t 0,T

выполня-

ются неравенства X1 t l ,

X2 t

,

то будет иметь ме-

сто интересующее событие для величины '

0.

Поскольку

2

координаты X1 t , X2 t броуновской точки A t

независимы, то

возможность осуществления с положительной вероятностью дан-

ных неравенств										можно проверять отдельно.	Вероятность
P	max		X		t					для очень больших значений T	и очень малых
	t 0,T			2

225

0 имеет величину порядка exp cT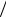 2 , c – некоторая посто-

янная. Видно, что данная вероятность быстро убывает, но всегда положительна, что и требовалось доказать. Теорема доказана. ▲ Рассмотрим теперь на траектории C плоского броуновского движения последовательность дуг A tn A tn 1 . Поскольку их

формы не зависят друг от друга, то из доказанной теоремы следует, что среди них почти достоверно найдутся такие, которые после соответствующего передвижения (или, даже, параллельного переноса) будут сколь угодно мало отличаться от любой наперед заданной

дуги. Это же замечание применимо к дугам A qn A qn 1 , q 0,1

при условии, что всякая дуга растягивается в q n2 раз. Дуги, обладающие, с точностью до гомотетии, формой, сколь угодно близкой к форме заданной непрерывной и конечной кривой L, таким образом, почти достоверно находятся на любой дуге траектории C.

Выберем в качестве L дугу с двойной точкой для того, чтобы доказать, что двойные точки образуют на кривой плоского бро-

уновского движения C всюду плотное множество.	Это означает
также, что двойные точки образуют и в плоскости	R2 всюду
	x1x2

плотное множество, ибо кривая плоского броуновского движения C, продолженная бесконечно1, всюду плотно заполняет всю плоскость.

Данное рассуждение не переносится автоматически на тройные точки, существование которых не очевидно. Про точки пересечения данного типа почти очевидно лишь одно утверждение: двойная точка, выбранная на C, никогда не может оказаться тройной. Это следует из доказанного утверждения, что случайно выбранная точка кривой C имеет нулевую вероятность оказаться двойной. Однако если даже случится, что кривая пройдет через некоторую фиксированную точку второй раз, это не увеличит вероятность того, что кривая C попадет в эту точку третий раз: вероятность такого события остается равной нулю. Аналогично, если существуют

1 Здесь подразумевается кривая плоского броуновского движения, полученная в результате бесконечно долгого движения броуновской точки.

226

тройные точки на кривой плоского броуновского движения C и известно, что некоторая точка A кривой C – тройная, то A не имеет никаких шансов оказаться четвертной точкой пересечения, и так далее.

Обобщая приведенные выше рассуждения, обозначим через En множество n -кратных точек кривой C, то есть множество всех точек, в которых кривая C пересекает саму себя n раз. На первый взгляд, представляется очевидным следующий вывод: при увеличении n множества En становятся все более и более разряженными и, вероятно, при достаточно больших n соответствующие множества становятся пустыми. Однако это неверно, что доказывает следующая ниже теорема, быть может, самая удивительная из теорем современного математического анализа.

Теорема 5.6.1 Множества En почти достоверно всюду плотны на кривой броуновского движения C, а следовательно, и в плоскости. Данное утверждение справедливо и для пересечения данных

+

множеств E En .

n 1

Более того, на кривой C существуют точки кратности, имеющей мощность континуума, то есть для такой точки A кривой C

множество значений t, при которых броуновская точка A t сов-

падает с A, имеет мощность континуума, и точки, обладающие указанной кратностью, также образуют всюду плотное множество! Это действительно примечательная особенность кривой плоского броуновского движения.

§6. Замыкание плоской броуновской кривой C

Лемма 5.1. Если в начальный момент времени t 0 подвижная броуновская точка находится в ограниченной области R2 , то математическое ожидание случайного времени ее первого выхода

1 Данная теорема в литературе часто называется теоремой Дворецкого – Эрдеша – Какутани.

227