Arkhiv_ZIP_-_WinRAR / Chast_3__Mat_an_2010_23_09

Бесконечно малые и бесконечно большие функции и их свойства

Функция α (x)

называется бесконечно малой в точке a , если limα (x) = 0 .

f (x)

x→a

a ,

Функция

называется

бесконечно

большой в точке

если

M

δ (M ) > 0 : x : 0 <

x −a

<δ

f (x)

> M .

Записывается

это

как

lim f (x)= ∞.

x→a

Свойства:

10 .

Если limα

(

x

)

= lim β

(

x

)

= 0 , то lim α

x

)

+ β

(

x

))

= 0 .

x→a

x→a

x→a ( (

20 .

Произведение бесконечно малой функции на ограниченную функцию есть

30 .

функция бесконечно малая.

Произведение бесконечно малых функций есть функция бесконечно малая.

40 .

Если lim f

(x)= A ≠ 0, limα

(x)= 0 , то lim

α(x)

= 0.

f (x)

x→a

x→a

x→a

50 .

Если α (x)

- бесконечно малая функция при x → a и α(x)≠ 0 при x ≠ a , то

1

- бесконечно большая функция при x → a . Если α(x) - бесконечно

α(x)

большая, то

1

- бесконечно малая.

α(x)

6˚. Произведение бесконечно большой функции на ограниченную функцию, не равную нулю, есть функция бесконечно большая.

7˚. Произведение бесконечно больших функций есть функция бесконечно большая.

Свойства функций, имеющих предел

	lim f (x) = A f (x) = A +α(x),						где limα(x) = 0;
	x→x0						x→x0
	lim ϕ (x) = B ϕ (x) = B + β(x),						где lim β(x) = 0
	x→x0						x→x0
Если lim f ( x) = A и lim ϕ(x) = B , то
x→x0				x→x0
1)	lim	( f (x) +ϕ (x)) = lim				f (x) + lim ϕ ( x);
	x→x0				x→x0	x→x0
2)	lim	( f (x) ϕ (x))= lim				f (x) lim ϕ (x);
	x→x0				x→x0	x→x0
3)	lim	(k f ( x))= k lim f ( x);
	x→x0			x→x0
		f (x)		lim f (x)
4)	lim		=	x→x0	, где ϕ (x) ≠α (x) .
		ϕ (x)		lim ϕ (x)
	x→x0
				x→x0

211

Если функции	y = f (x) и	y =ϕ (x)	имеют одну область определения D и
x D f (x)≤ϕ(x), то lim f (x) ≤ lim ϕ(x).
	x→x0	x→x0
Теорема о пределе промежуточной функции.
Если 1) x D	f (x)≤ϕ(x)≤ g (x), 2)		lim f (x) = lim g(x) = A ,
			x→x0	x→x0
то lim ϕ(x) существует и lim ϕ(x) = A.
x→x0		x→x0

Замечательные пределы
Первый замечательный предел	0		: lim sin x				=1.
0			x→0		x		x
∞					+	1
Второй замечательный предел 1 : lim 1						x	= e ;
			x→∞
lim ( f (x))ϕ ( x)							lim ϕ ( x)
			= lim f (x) x→x0
0				0
x→x			x→x

lim(1 +t )1/ t = e .

t→0

.

Сравнение бесконечно малых функций

	Для бесконечно малых выполняется:			α1 (x)
	1) α1(x) и α2(x)- одного порядка, если lim						= A ,		A < ∞;
		x→x0		α2 (x)
	2) α1(x) α2(x) - эквивалентные, если lim			α1(x)			=	1;
		x→x0		α2 (x)
	3) α1(x) = о(α2(x)) - α1(x) является	бесконечно						малой более высокого
	порядка малости по сравнению с α2(x), если		lim		α1	(x)		= 0 ;
					α2	(x)
			x→x0
	4) если α1(x) α2(x), α3(x) α4(x), то	lim	α1 (x)			= lim			α2 (x) .
		x→x0	α3 (x)				x→x0		α4 (x)

Эквивалентные бесконечно малые при x → 0:

1 −cos x

x2

,

1 ± x −1

±

x

, a

x

−1

x ln a ,

2

2

x

loga (1 + x)

, (1 + x)α −1 αx .

ln a

Ряд эквивалентных бесконечно малых при x → 0:

x sin x arcsin x tg x arctg x sh x ex – 1 ln(1 + x).

Некоторые пределы:
lim	log	a	(1+ x)	=	1	,	a > 0, a ≠1, lim	ax −1	= ln a, a > 0	,
			x		ln a			x
x→0							x→0

212

lim (1 + x)a −1 = a , lim				1 + x −1	=	1 .
x→0	x	x→0		x		2
		НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Три эквивалентных определения непрерывности функции в точке:
1. Пусть	функция	y = f (x)		определена на множестве D и пусть			точка
x0 D .	Функция	y = f (x) называется непрерывной в точке x0 ,					если
выполнены условия:
1) f (x0 ) , 2) lim f (x) , 3)				lim f (x) = f (x0 ) .
	x→x0			x→x0

2.Функция y = f (x) называется непрерывной в точке x0 , если функция

определена в точке x0	и при этом lim ∆y = 0 , то есть бесконечно малым
	∆x→0

приращениям аргумента соответствуют бесконечно малые приращения функции.

3.Функция y = f (x) называется непрерывной в точке x0 , если функция

определена	в	точке x0 ,	существуют		односторонние пределы
lim f (x),	lim	f (x) и при этом	lim	f (x) = lim f (x) = f (x0 ) .
x→x0 −0	x→x0 +0		x→x0 −0	x→x0	+0

Два определения односторонней непрерывности:

1.Функция y = f (x) называется непрерывной в точке x0 слева, если

функция определена	в точке x0 и существует односторонний предел
lim f (x) и при этом	lim f (x) = f (x0 ) .
x→x0 −0	x→x0 −0

2.Функция y = f (x) называется непрерывной в точке x0 справа, если

функция определена в точке x0 и существует односторонний предел

lim	f (x) и при этом x→limx +0	f (x) = f (x0 ) .
x→x +0	0
0
Функция,	непрерывная в любой точке множества D , называется

непрерывной на множестве D .

Свойства непрерывных функций

1.Если функции y = f (x) и y =ϕ(x) определены на множестве D и

непрерывны в точке x0 D , то функции f (x)+ϕ(x), k f (x), f (x) ϕ(x),

	f (x)	непрерывны в точке x , причем частное требует условия ϕ(x )≠ 0 .
	ϕ(x)
		0	0

2.Если f (x) непрерывна на [a,b], то она ограничена на этом отрезке.

213

3. Если f (x) непрерывна на [a,b], то она достигает на нем своих точной верхней и точной нижней граней

( x1 [a,b]: f (x1 ) = M , x2 [a,b]: f (x2 ) = m ).

4. О прохождении непрерывной функции через ноль. Если функция

y = f (x) непрерывна на [a,b] и имеет на концах отрезка значения f (a) и

f(b) разных знаков, то найдется точка ξ (a,b) такая, что f (ξ) = 0 .

5.О прохождении непрерывной функции через любое промежуточное значение. Если функция y= f (x) - непрерывна на [a,b], имеет на концах отрезка значения f (a) = A, f (b) = B и число С расположено между числами

Аи В : A < C < B , то найдется точка ξ (a, b) такая, что f (ξ) = C .

Теорема применяется для отыскания корней уравнения вида F(x) = 0 методом половинного деления отрезка.

6.Непрерывность обратной функции. Если:

1)y = f (x) - строго монотонная, непрерывная на [a,b],

2)α = f (a), β = f (b) , то x = f −1( y) - строго монотонная, непрерывная на [α, β].

7.Если исходные функции непрерывны, то в результате их сложения, вычитания, умножения, деления (если знаменатель ≠ 0 ), взятия сложной функции получаются непрерывные функции.

8.Для непрерывной в точке x0 функции f (x) справедливо:

lim f (x) = f (x0 ) = f (lim x) .
x→x0	x→x0

9.Для непрерывных функций переходить к пределу можно под знаком

функций:

а) lim ex	2	lim x2	= e25 ,
		= ex→5
x→5

б) limln(1 +sin x) = ln(lim(1 +sin x)) = ln(1+ 0) = 0 .
x→0	x→0

Классификация точек разрыва

1.Если односторонние пределы существуют и равны,

lim f (x) =	lim f (x),
x→x0 −0	x→x0 +0

а функция y = f(x) не определена в точке x0, или lim f ( x) ≠ f (x0 ), то

x→x0

точка x0 называется точкой устранимого разрыва.

Устранимый разрыв можно устранить, вводя функцию

	f (x),		x ≠ x ,
f1			0
	( x) = lim f ( x), x = x .
		0	0
	x→x

2.Если: односторонние пределы существуют, конечны, но не равны,

lim f (x) ≠	lim f (x),
x→x0 +0	x→x0 −0

214

то точка x0 называется точкой разрыва 1-го рода (неустранимый конечный скачок).

3.Если хотя бы один из односторонних пределов не существует или бесконечен, то точка x0 называется точкой разрыва 2-го рода.

ПРОИЗВОДНАЯ ФУНКЦИИ

Производной функции f (x) в точке x называется lim					∆y	при условии, что он
				∆x→0	∆x
существует. Обозначение: y′ = dy	= lim	∆y	= lim	f (x + ∆x) − f (x)			.
		∆x
dx	∆x→0		∆x→0	∆x

Геометрический смысл производной.

Уравнение касательной к кривой y = y(x) в точке x0 : y − y0 = y′(x0 ) (x − x0 ).

	Уравнение нормали имеет вид:
	y = f (x0 ) +	−1	(x − x0 ) , f (x	)≠ 0 .
		f ′(x0 )
			0

Правила и формулы дифференцирования

1)(c)′ = 0 , c = const ;

2)( f (x) ± g(x))′ = f ′(x) ± g′(x) ;

3)(c f (x))′ = c f ′(x) ;

4)( f (x) g(x))′ = f ′(x) g(x) + g′(x) f (x) ;

f (x)

′

′

′

5)

=

f (x)g(x) − g (x) f (x)

,

g (x)≠ 0 .

g(x)

g

2

(x)

Производная обратной функции: (f −1 ( y))′y=y0

=

1

f ′(x0 )

Производная сложной функции: y = f (u), u =ϕ(x) , тогда y ′

= y

′u ′

1

x

u

x

Логарифмическая производная:

ln y = ln f (x),

[ln y]x′ =

y′,

y′ = y [ln y]′.

y

Производная функции, заданной параметрически:

x = x(t)

′

y = y(x)

yx′ =

yt

.

y = y(t)

x ′

t

215

	Таблица производных (с учетом u =ϕ(x) )
1.	(uα )′ =α xα −1 u′.
2.	(au )′ = au ln a u′ (a > 0, a ≠1) (eu )′ = eu u′.

3.(loga u)′ = loga e u1 u′ (a > 0, a ≠1) (ln u)′ = u1 u′.

4.(sin u)′ = cosu u′.

5.(cosu)′ = −sin u u′.

6.(tgu)′ = cos12 u u′.

7.(ctgu)′ = −sin12 u u′.

8.	(arcsin u)′ =			1	u′.
				−u2
	1
9.	(arccosu)′ = −			1		u′.
				1 −u2

10.(arctgu)′ = 1 +1u2 u′.

11.(arcctg u)′ = −1 +1u2 u′.

12.	(shu)′ = chu u′.					Гиперболический синус shx =	ex −e−x		.
						2
13.	(chu)′ = shu u′.					Гиперболический косинус chx =		ex + e−x		.
						2
14.	(thu)′ =	1		u′		Гиперболический тангенс thx = chshxx .
		ch2u
15.	(cthu)′ =		1		u′	Гиперболический котангенс cthx = chshxx .
			sh2u

216

		Производные высших порядков
	Производная второго порядка:				′′	′	′
					f (x) = (	f (x)) .
	Производная n -го порядка:		f (n) (x) = (f (n−1) (x))′или					y(n) (x) = d n yn .
									dx
	Производные функции, заданной параметрически:
	x = x(t)		y ′					(y′x )	′
	y = y(x)	yx′ =	t		- первая,	y′′xx = (y′x )′x =		t	−вторая.
			x ′
	y = y(t)							xt′
			t

Правила вычисления производной n-го порядка

1.[f (x) + g(x)](n) = f (n) (x) + g(n) (x) .

2.Формула Лейбница (производная произведения):

	n	n!
	[f ( x) g( x)]( n) = ∑Cnk f ( n−k ) ( x) g( k ) ( x) , где Cnk =			– число сочетаний
		k!(n − k)!
	k =0
	из n по k , n!= n(n −1)(n − 2).....3 2 1, 0!=1!=1.

Классификация функций

			Функции
Элементарные функции								Специальные
									функции
Алгебраические				Трансцендентные
функции					функции
Рациональные			Иррациональные
функции				функции

217

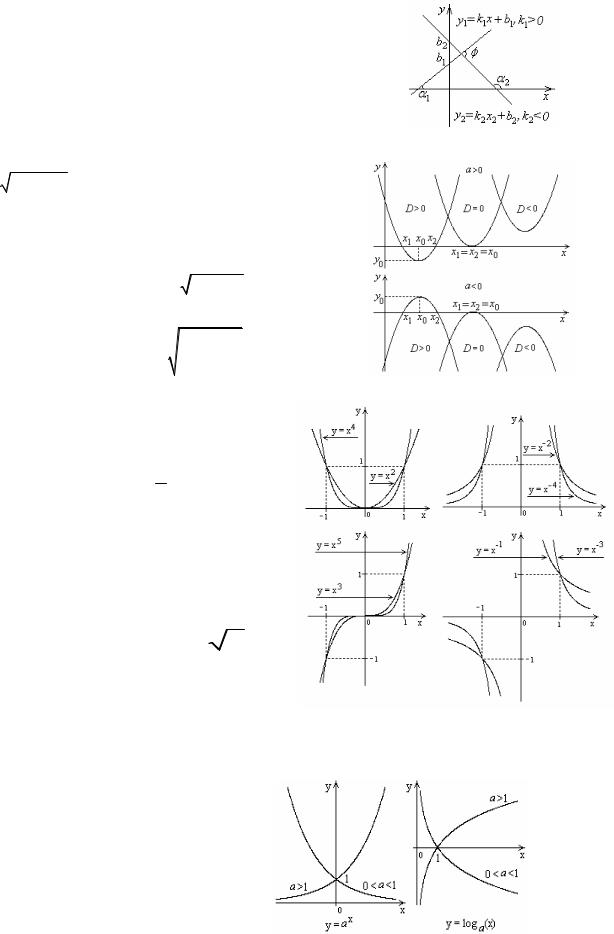
					Графики элементарных функций
	1. Линейная функция: y = kx +b .
k	= tgα , k	2	= tgα	2	, tgφ = tg(α	2	−α	) =			k2 −k1		,
1	1						1		1		+ k1 k2
k1	k2 = −1 - условие перпендикулярности прямых.

2.Квадратичная функция: y = ax2 +bx + c, a ≠ 0 .

x1,2

=

−b ± b2 − 4ac ,

D = b2 − 4ac ,

x0 = −

b

,

2a

2

y

0

= 4ac −b2 .

4a

ax

2

+ 2mx + c = 0

→ x =

−m ±

m2 − ac

1,2

a

x2 + px + q = 0 → x = −

p

±

p 2

− q

1,2

2

2

ax2 +bx + c = a(x − x1 )(x − x2 ) .

x + x = −b ,

Теорема Виета: 1 2 a

x1 x2 = ac .

	3. Степенные функции.
	3.1. y = xn , n N .	3.2. y =			1	, x ≠ 0 .
					xn
		1
	3.3. Иррациональные y	= x	n	=	n	x .

Трансцендентные функции

4.Показательная y = ax , a > 0, a ≠1.

5.Логарифмическая

y = loga x, a > 0, a ≠1, x (0,∞) .

218

6. Тригонометрические функции

6.1.y = sin x .

6.2.y = cos x .

6.3.y = tg x, x ≠ π2 + nπ .

6.4.y = ctgx, x ≠ kπ .

7. Обратные тригонометрические функции

7.1.y = arcsin x, | x |≤1. arcsin(−x) = −arcsin x .

7.2.y =arccosx, | x|≤1. arccos(−x) =π −arccos x .

7.3.y = arctg x , arctg(−x) = −arctg x .

7.4.y = arcctg x .

arcctg(−x) =π −arcctg x . arcsin x + arccos x = π2 ,

arctg x + arcctg x = π2 , arctg x = π2 −arctg 1x .

219

8.Гиперболические функции

8.1.Гиперболический синус

y =sh x = ex −e−x .

2

8.2.Гиперболический косинус y = ch x = ex +2e−x .

8.3.Гиперболический тангенс

	y = th x =	ex −e−x	=	sh x	.
		ex + e−x		ch x

8.4. Гиперболический котангенс

	y = cth x =	ex + e−x	=	ch x	.
		ex −e−x		sh x

sh2 x −ch2 x =1, th x cth x =1,

sh(x + y) = sh x ch y +sh y ch x , ch(x + y) = ch xch y +sh xsh y .

Формулы исследования функций с помощью производной. Асимптоты

	1) x = x0		- вертикальная асимптота y = f (x), если					lim f	(x)= ±∞.
								x→x0 ±0	y = f (x), если
	2) y =b		- правая (левая)			горизонтальная	асимптота
	lim	f (x)= b .
	x→±∞			f (x)
	3)	y = kx +b , k = lim			,	b = lim f (x)	−kx	- наклонная асимптота
				x
			x→+∞			x→+∞
	y = f (x) при x → +∞.

220