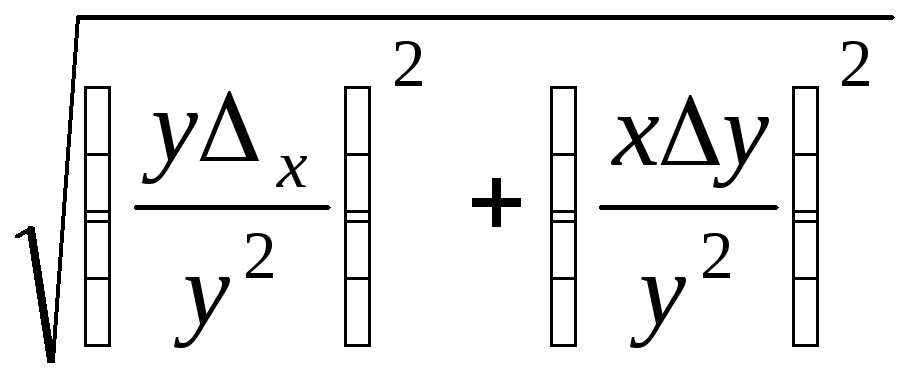1. Погрешности измерений

Всякое измерение, как бы тщательно оно ни проводилось, дает лишь приближенный результат и не может не содержать ошибок (погрешностей измерения).

Пусть произведено n измерений некоторой физической величины х, в результате которых получен ряд значений этой величины: х₁, х₂, …, х_n. Выполнив измерения, необходимо привести не только полученный результат, но и дать информацию о его точности. В подавляющем большинстве случаев наилучшей оценкой величины х, основанной на измерениях значений х₁, х₂, …, х_n, является среднее арифметическое результатов измерений <x>. При этом необходимо указывать интервал значений измеряемой величины +х, в пределах которого с определенной вероятностью может оказаться истинное значение измеряемой величины: х + х есть наибольшее вероятное значение измеряемой величины, х-х – наименьшее.

Величина х называется погрешностью или ошибкой результата, интервал от х+х до х-х – доверительным интервалом. Вероятность того, что среднее значение х отличается от истинного не более, чем на х – называется доверительной вероятностью Р.

Она равна доле результатов однотипных серий измерений, попадающих в пределы доверительного интервала, т.е. отличающихся от истинного значения не более, чем на х. Обычно ошибки измерения находятся для определенной вероятности Р₀. Для обеспечения более надежного совпадения измеренного результата с истинным значением величины может быть введена большая вероятность Р. В этом случае устанавливается доверительный интервал с границами + = kх, где коэффициент k определяется отношением Р/Р₀. Доверительные границы  определяются по заданной вероятности Р того, что на числовой оси отрезок 2 с центром в точке х включает значение измеряемой величины х.

Если в результаты измерений введены все известные поправки к показаниям приборов и устранены грубые ошибки или промахи, то среднее арифметическое исправленных результатов измерений вычисляется по формуле:

Обычно в качестве общепринятой стандартной погрешности измерения принимается среднеквадратичная ошибка. Она равна дисперсии распределения Гаусса для случайных величин, которое считается хорошим приближением к распределению ошибок измерения.

Среднее квадратичное отклонение среднего арифметического результата измерения

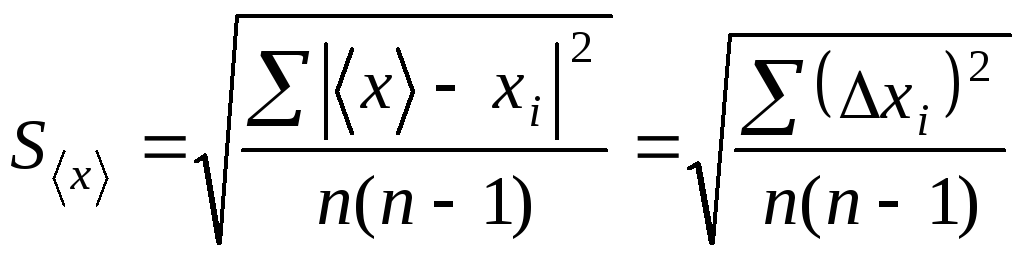
Среднее квадратичное отклонение S_<x> характеризует погрешность среднеарифметического <x>. Запись в виде х = + S_<x> означает, что в 68 % случаев результаты любых последующих измерений <x>, выполненных с такой же тщательностью, попадут в интервал (<x>-S_<x> , <x>+S_<x>). Другими словами, полученный результат будет находится в пределах ±S_<x> от правильного результата с доверительной вероятностью Р=68 %. Вероятность того, что результат измерения окажется в пределах +2S_<x> равна 95,4%; в пределах +3S_<x> - 99,7%.

Распределение ошибок измерения совпадает с распределением Гаусса только при бесконечно большом числе измерений. При конечном числе измерений вычислить доверительные границы случайной погрешности результата измерения можно при помощи так называемого распределения Стьюдента

 = + t_p,n S_<x>

где +t_p,n – коэффициент Стьюдента для числа наблюдений n и доверительной вероятности Р, определяемый по таблице коэффициентов Стьюдента.

Таблица коэффициентов Стьюдента

Р – доверительная вероятность

n – число измерений

n\P	0,5	0,6	0,7	0,8	0,09	0,95	0,0989	0,999
2 3 4 5 6 7 8 9 10 15 20 40 60 120	1 0,82 0,77 0,74 0,73 0,72 0,71 0,71 0,70 0,69 0,69 0,68 0,68 0,68 0,67	1,38 1,06 0,98 0,94 0,92 0,90 0,90 0,90 0,88 0,87 0,86 0,85 0,85 0,85 0,84	2,0 1,3 1,3 1,2 1,2 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,0 1,0 1,00	3,1 1,9 1,6 1,5 1,5 1,4 1,4 1,4 1,4 1,3 1,3 1,2 1,3 1,3 1,3	6,3 2,9 2,4 2,1 2,0 1,9 1,9 1,9 1,8 1,8 1,7 1,7 1,7 1,7 1,6	12,7 4,3 3,2 2,8 2,6 2,4 2,4 2,3 2,3 2,1 2,1 2,0 2,0 2,0 2,0	31,8 7,0 4,5 3,7 3,4 3,1 3,00 2,9 2,8 2,6 2,5 2,4 2,4 2,4 2,3	636,6 31,6 12,9 8,6 6,9 6,0 5,4 5,0 4,8 4,1 3,9 3,6 3,5 3,4 3,3

Как видно из таблицы уже при числе измерений 7-10 можно пользоваться среднеквадратичной ошибкой как и при бесконечно большом числе измерений. При автоматизированных измерениях число измерений может быть очень большим, однако увеличение числа измерений приводит лишь к уменьшению среднеквадратичной ошибки и не изменяет доверительной вероятности в пределах интервала этих ошибок.

Ошибки можно разделить на два типа: систематические и случайные. Основное различие между ними заключается в том, что систематические погрешности остаются постоянными по величине и знаку; случайные погрешности, наоборот, непредсказуемым образом изменяют свою величину и знак. Случайные погрешности можно уменьшить с помощью многократных измерений. Систематические ошибки таким способом уменьшить нельзя. Случайные погрешности можно обрабатывать статистическими методами, к систематическим погрешностям эти методы неприменимы.

Систематические ошибки возникают вследствие погрешностей измерительной аппаратуры (отстающий секундомер, вытянутая линейка, стрелочный прибор, у которого стрелка до начала измерений не была установлена на нуль), отличия условий эксперимента от предполагаемых теорией, несовершенства методики эксперимента. Общих правил для определения систематических ошибок не существует; в каждом конкретном случае их выявление требует специальных исследований. Полностью исключить систематические ошибки нельзя, можно лишь перевести их в разряд случайных.

Случайные ошибки всегда присутствуют в эксперименте и являются результатом суммарного действия большого количества факторов, влияние каждого из которых в отдельности учесть практически невозможно. Типичные источники случайных погрешностей: небольшие ошибки наблюдателя, небольшие помехи, воздействующие на аппаратуру (например, механические вибрации) и другие. Случайные погрешности нельзя исключить, но их влияние можно учесть с помощью многократных измерений с последующей математической обработкой результатов измерений.

Разновидность случайных ошибок - грубые ошибки или промахи. Они возникают вследствие невнимательности экспериментатора (например, неправильные отсчеты по прибору, неправильная запись отсчета и т.п.). В большинстве случаев при многократных измерениях промахи хорошо заметны, так как соответствующие им отсчеты сильно отличаются от других. При обработке результатов такие отсчеты следует отбрасывать.

Доверительные границы общей погрешности результата измерения с учетом систематической погрешности

где  - систематическая погрешность, которая в условиях учебной лаборатории оценивается по цене деления шкалы или указывается на приборе. В некоторых случаях доверительные границы общей погрешности рассчитывается по формуле.

x=

Окончательный результат измерения записывается в виде

х=<x>x; P

Например, ρ = (7,700,72)*10³кг/м³, Р=0,95.

Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и первая значащая цифра доверительных границ x. Доверительные границы записываются с двумя значащими цифрами.

Относительная погрешность результата измерения, характеризующая точность измерений.

%

Оценка погрешности результатов косвенных измерений.

Искомая величина вычисляется по расчетной формуле.

<y>=f (<x₁>,<x₂>,…,<x _n>),

при подстановке в нее средних значений измеренных величин. Абсолютная ошибка косвенных измерений находится по обычному правилу нахождения полного дифференциала функции, в который вместо дифференциалов переменных подставляются значения полученных ошибок. При этом все знаки - в формуле дифференциала заменяются на “+”. Например, косвенно измеряемая величина

y= f (x_1, x₂,…z₁ z₂…)

где x₁, x₂….. непосредственно измеряемые величины, z₁, z₂….. принятые табличные значения известных величин.

Тогда абсолютная погрешность.

y=

В качестве погрешностей табличных значений берется половина последней значащей цифры, однако обычно эта величина оказывается много меньше ошибок измерений и ее можно не учитывать.

Относительная погрешность определяется как отношение абсолютной погрешности к измеренной величине как и для прямых измерений. Можно, однако, находить относительную погрешность, не определяя абсолютную.

Для этого надо.

А) прологарифмировать расчетную формулу.

y= f (x₁, x₂,… x _n );

В) Найти полный дифференциал от lny

d(lny)=

Производная от lny=, а дифференциал соответственно представляет собой сумму относительных погрешностей по всем измеренным значениям.

Относительная погрешность косвенного измерения находится как сумма относительных погрешностей прямых измерений

=

При расчете ошибок косвенных измерений, когда исходные ошибки независимы и случайны, производится их квадратичное сложение.

Окончательный результат записывается в виде

В таблице приводятся некоторые формулы для нахождения погрешностей величины, являющейся простой функцией других величин.

Таблица относительных погрешностей косвенных измерений

Вид функции	Абсолютная погрешность	Относительная погрешность
X Y Z
ln x