1. Определение модуля Юнга методом растяжения

1. Микрометром несколько раз измерить диаметр проволоки d в различных местах. Результаты занести в таблицу 1.

Таблица 1

di, мм	<d>, мм	 di, мм	(di)^2	Sd мм	d	d, мм	d, мм

2. Измерить длину рабочего участка проволоки l_o. Нагружая плат­форму дисками, снять показания индикаторов ₁ и ₂ и массу дис­ков т, те же измерения провести при разгружении платформы.

Результаты измерений занести в таблицу 2.

Таблица 2

S, мм

L0, мм

m, кг

M, кг

, H/м^2

Нагружение

Разгружение

1

2

lн

н

1

2

lн

н

3. Заполнить таблицу 1 в соответствии с правилами обработки результатов прямых измерений. Доверительную вероятность при­нять равной Р=0,67, в этом случае коэффициент Стьюдента t = l. Доверительный интервал d рассчитать по формуле

где _d — погрешность микрометра.

По среднему значению диаметра найти площадь сечения про­волоки S.

4. Для каждой строки таблицы 2 рассчитать суммарную массу дисков М, растягивающих проволоку; напряжение  = Mg/S; удли­нение проволоки при нагружении и разгружении l=_i—_z; отно­сительную деформацию = 1/1_о.

5. Построить на миллиметровой бумаге график зависимости  от .

Найти модуль Юнга Е, как тангенс угла наклона графика к оси абсцисс

Е=/.

6. Определить относительную погрешность измерения модуля Юнга:

где S_e — среднее квадратическое отклонение модуля Юнга по случайному разбросу точек; ₁ - погрешность линейки.

Вычислить доверительный интервал измерения модуля Юнга

_Е=  Е.

Записать окончательный результат в виде

Е = <Е> ±_е, Р = 0,67.

2. Определение модуля упругости методом изгиба

Рассмотрим изгиб однородного бруска (балки) произвольного поперечного сечения, которое должно оставаться одинаковым на протяжении всей длины бруска. Пусть до деформации брус имел прямолинейную форму. Проводя сечение АВ и А' и B' нормальные к оси бруска, мысленно вырежем из него бесконечно малый элемент AA' и ВВ' длина которого l₀(рис. 5).

Рис. 5

Ввиду бесконечной малости выделенного элемента можно считать, что в результате изгиба прямые АА', NN', ВВ' и все прямые, параллельные им, перейдут в окружности с центрами на оси 0, перпендикулярной к плоскости рисунка (рис.6). Эта ось называется осью изгиба. Наружные волокна, лежащие выше линий NN при изгибе удлиняются, волокна лежащие ниже линии NN'—укорачиваются. Длина линии NN' остаётся неизменной. Эта линия называется нейтральной линией.

Рис. 6

Проходящее через неё сечение (не деформированного) бруса плоскостью, перпендикулярной к плоскости рис.6, называется нейтральным сечением.

Таким образом, все наружные волокна будут растянуты, все внутренние – сжаты. Пусть R - радиус кривизны нейтральной линии NN. Тогда l₀=R*, где  - центральный угол, опирающийся на дугу NN.

Рассмотрим волокно бруса, находящееся на расстоянии , от нейтрального сечения. Величина  положительна, если волокно находится выше нейтрального сечения (рис.6) и отрицательно, если оно находится ниже. Если брус не слишком толст, так что //<<R то длина рассматриваемого волокна будет l=(R+)*, а удлинение:

l=l-l₀=*

Следовательно, напряжение, действующее вдоль рассматриваемого волокна

Напряжение, таким образом, меняется линейно с расстоянием . Ниже нейтрального сечения оно отрицательно, то есть является давлением. Сумма сил напряжения или сжатия одинаковая для всех волокон. Она может быть учтена особо и исключена из рассмотрения, когда речь идет об изгибе в чистом виде. Поэтому мы будем считать, что сумма всех сил натяжения, действующих в каждом нормальном сечении бруса, равна нулю, то есть или   dS = 0 или   dS = 0, где dS – элемент площади рассматриваемого поперечного сечения. Интегрирование ведется по всему поперечному сечению бруса. Очевидно, что нейтральная линия и нейтральное сечение проходят через центр тяжести поперечного сечения бруса. Из соотношения  dS = 0 следует, что момент сил напряжения М, действующих на сечение В, не зависит от того, относительно какой оси он берется. Для вычисления М проще всего взять ось, перпендикулярную к плоскости рисунка и проходящую через точку N. Очевидно,

где I = ²  dS

Величина I называется моментом инерции поперечного сечения бруса по аналогии с соответствующей величиной, вводимой при рассмотрении вращения тела вокруг неподвижной оси. Однако, в отличие от последней, I есть чисто геометрическая величина с размерностью четвертой степени длины. Если поперечное сечение бруса имеет форму прямоугольника с шириной а и высотой, b , то

Действительно, dS = а  d (рис. 6). Значит

Направим ось Х вдоль нейтральной линии недеформированного бруса. Ось Y направим к ней перпендикулярно и расположим в плоскости изгиба. Тогда уравнение нейтральной линии изогнутого бруса можно представить в виде y = y(x). По известной формуле

если изгиб мал (Y<<1) то квадратом первой производной можно пренебречь. В этом приближении

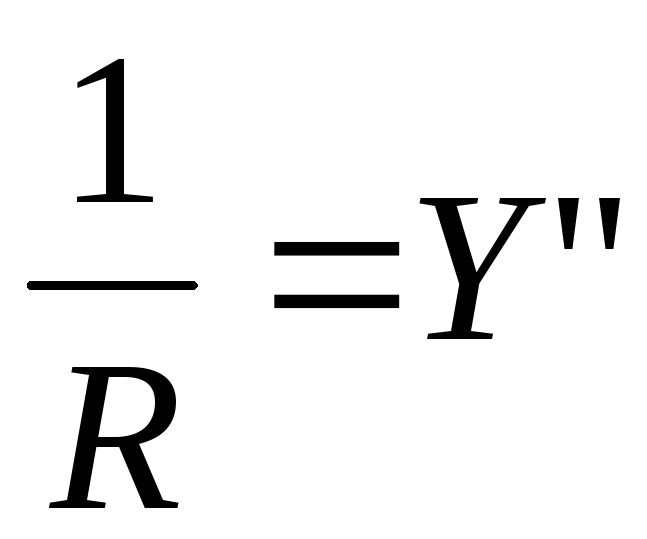М =Е  I  Y

Определим теперь стрелу прогиба балки, жестко закрепленной в стене одним из своих концов (рис. 7).

Рис. 7

На другой конец балки действует сосредоточенная сила F. Весом самой балки будем пренебрегать. Стрелой прогиба мы называем смещение свободного конца балки под действием приложенной силы F. Поместим начало координат в точке О, в которой нейтральная, линия балки пересекается с плоскостью стены. Через произвольную точку В(х) (с координатой х=(В) проведем нормальное сечение. Для равновесия необходимо, чтобы сила F действующая на часть ВА со стороны части OВ, была направлена вверх и равнялась F . Вместе с О она образует пару сил с моментом М == F(l – х), где l - длина балки.

Момент силы напряжения возьмём в приближённом виде, считая, что прогиб мал. Это приводит к уравнению

E  I  Y"=F (l-x)

Ось Y направлена в сторону вогнутости, то есть вниз. При таком условии вторая производная Y" положительна, и обе части последнего соотношения имеют одинаковые знаки. Интегрируя это уравнение один раз, получим

Постоянная интегрирования С равна нулю, так как при х = 0, то есть в точке О, касательная к нейтральной линии горизонтальна. Интегрируя вторично и учитывая, что в точке О (то есть при х = 0) у=0, найдём

Полагая здесь x =l находим стрелу прогиба (у=)

 = Fl³ / 3EI

Учитывая что , получим =F l³4 /аb³Е

По стреле прогиба  при данной сосредоточенной нагрузке F и зная размеры бруса, можно определить модуль Юнга материала бруса:

Е=4 F  l³ /аb³

Рис.8

Прибор рис.8 представляет собой раму, установленную на опорах. На раме установлен индикатор, который может перемещаться вдоль рамы и служит для измерения величины прогиба бруса. Брус закреплён с одной стороны неподвижно. На незакреплённой стороне бруса имеется опорная призма с подвеской для гирь. Она также может перемещаться вдоль бруса.

1. Установите опорную призму в месте, где кончается сужение бруса (сдвинуть призму вдоль стержня влево до упора).

2. Измерьте микрометром высоту бруса в нескольких местах и найдите его среднее значение.

3. Измерьте длину стержня (расстояние от места закрепления до опорной призмы).

4. Измерьте штангенциркулем ширину бруса в месте его закрепления и в месте подвеса грузов и найдите среднее значение по формуле:

5. Установите стрелку индикатора на нуль и постепенно нагружайте стержень дополнительным и грузами (1 кг, 2 кг, З кг и т.д.) делая каждый раз отсчет по индикатору.

6. Снимая дополнительные грузы в обратном порядке, снова зафиксируйте показания индикатора.

7. Проделайте изложенное в пунктах (5) и (6) по 3 раза.

8. Данные измерений занесите в таблицу

Р(кГ) (мм)	№	1	2	3	4	5
	1.
	2.
	3.
	4
ср (мм)

9. По данным измерений постройте график зависимости _ср —f(F) проверьте, выполняется ли закон Гука.

10. Вычислите модуль Юнга стали для нагрузки F=5кГ и сравните полученный результат с табличным значением.

11. Вычислите абсолютную и относительную погрешности измерения.