3. Дистрибутивности:

Правый и левый дистрибутивные законы умножения относительно сложения: (а + в)с = ас + вс; с(а + в) = са + св;

Правый и левый дистрибутивные законы умножения относительно вы­читания: (а - в)с = ас - вс; с(а - в) = са - св.

Доказательство. 1. Докажем коммутативный закон сложения. Построим такие ко­нечные множества А и В, что п(А) = а, п(В) = в и АВ = . Для любых множеств справед­лив коммутативный закон объединения АВ = ВА (доказано ранее). Равные конечные множества имеют равные численности, т.е. п(АВ) = п(ВА). По определению суммы целых неотрицательных чисел п(АВ) = п(А) + п(В) = а + в, п(ВА) = п(В) + п(А) = в + а. Следовательно, а + в = в + а верно для любых целых неотрицательных чисел.

2. Доказательство ассоциативного закона сложения опирается на ассоциативность объединения множеств А, В и С проводится аналогично доказательству предыдущего закона.

3. Доказательства остальных законов проводятся аналогично. Теорема доказана.

Заметим, что коммутативный и ассоциативный законы сложения распрост­раняются на любое конечное число слагаемых, а коммутативный и ассоциатив­ный законы умножения справедливы для любого конечного числа множителей.

Дадим теоретико-множественное обоснование правила вычитания суммы из числа. С этой целью рассмотрим три конечных множества А, В и С таких, что п(А) = а, п(В) = в, п(С) = с, ВС=  и ВС А. Тогда а - (в + с) = п(А\( ВС), а (а- в) - с = п((А\В)\С). На диаграммах Эйлера-Венна множество А\(ВС) пред­ставлено заштрихованной частью на рис.а, а множество (А\В)\С - двояко зашт­рихованной частью на рис.б. Сравни­вая указанные области, убеждаемся в том, что они одинаковы. Значит, для вышеука­занных множеств А, В и С выполняется равенство А\(ВС) = (А\В)\С. Следова­тельно, п(А\(ВС)} = п{(А\В)\С), т.е. а - (в + с) = (а - в) - с. Аналогично рас­суждая, можно дать теоретико-множественное обоснование остальным правилам.

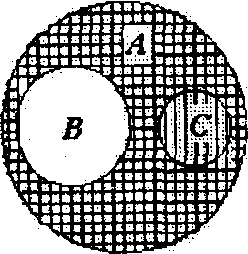
Правила деления суммы, разности и произведения на число также имеют теоретико-множественное обоснование. Пусть а = п(А), в = п(В) и АВ = . Если каждое из множеств А и В можно разбить на с подмножеств, то очевидно, что их объединение АВ также разбивается на с подмножеств. При этом, если каждое подмножество в разбиении множества А содержит а: с элементов, каж­дое подмножество в разбиении В - в:с элементов, то каждое подмножество в разбиении объединения содержит а:с + в:с элементов. Это означает, что (а + в):с = а:с + в:с. Аналогично рассуждая, можно дать теоретико-множествен­ное обоснование остальным правилам.

МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ Z. Практическая деятельность и потребности самой математики приводят к необходимости расширения множества неотрицательных чисел. Так, температура воздуха 1° не определяет нагретость воздуха без указания - 1° холода или тепла, информация "АЗС находится в 2 км от перекрестка" не определяет ее местонахождения, т.к. не указано, в какую сто­рону от перекрестка надо двигаться к АЗС: влево или вправо, и т.п. В математи­ке также имеется ряд задач, неразрешимых во множестве целых неотрицатель­ных чисел. Например, никакое целое неотрицательное число х не может быть решением уравнения в + х = а, если а < в и а, в ₀. Неразрешимость таких задач приводит к необходимости расширить множество ₀.

Числа вида -п, где п₀, называются отрицательными целыми числами. Множе­ство всех отрицательных целых чисел обозначают символом Z_. Числа п и -п назы­ваются противоположными, причем считают, что -(-п) = п. Число 0 не относится ни к положительным, ни к отрицательным числам. Противоположные числа на число­вой оси изображаются точками, симметричными относительно начала координат.

Объединение множеств ₀, Z_ и {0} называют множеством целых чисел и обозначают символом Z.

АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НА МНОЖЕСТВЕ Z .

Модуль (абсолютная величина) числа п - само это число, если оно неотрицательно, и противоположное ему число -п, если оно отрицательно (обо­значается |п|), т.е.

п, если п ₀

IпI

-п если п Z_.

Теорема 8.34. Для п  Z выполняются следующие равенства:

1) -пg = (-1 )-п; 5) (-п)*т = -п*т;

2) (-1)*(-1 ) = 1; 6) п - т = п + (-т) = -(т - п);

3) -(-л) = п; 7) (-п) + (-т) = - (п + т);

4) (-п)*(-т) = п*т; 8) -0 = 0.

Доказательство этой теоремы опускается.

Данные свойства позволяют сформулировать правила сложения и умноже­ния целых чисел, которые можно считать определениями данных операций.

Правило 1. (Правило сложения).При сложении двух целых чисел с одинаковыми знаками получается число того же знака, модуль которо­го равен сумме модулей слагаемых. При сложении чисел с разными знаками получается число, знак которого совпадает со знаком слагае­мого, имеющего больший модуль, а модуль равен разности модулей слагаемых. Сумма противоположных чисел равна нулю, а сумма дан­ного числа и нуля равна данному числу.

Правило 2. (Правило умножения).При умножении двух целых чисел получается число, модуль которого равен произведению модулей мно­жителей, а знак положителен, если знаки множителей одинаковы, и отрицателен, если множители имеют разные знаки. Если хотя бы один из множителей равен нулю, то произведение равно нулю.

Операция вычитания в силу свойства 6 теоремы 8.34 сводится к операции сложения.

Разность двух целых чисел п и т- целое число r, вычисляемое по правилу:

r = п + (-т), т.е. разность двух целых чисел п и m есть сумма целого числа п и числа (-т), противоположному числу т. Разность чисел п и т записывают в виде п- т, число и называют уменьшаемым, а число т - вычитаемым.

Множество Z замкнуто относительно операций сложения, умножения и вычитания.

Частное отделения целого числа п на целое число т — такое целое число р (если оно существует), которое удовлетворяет равенству п = т р. Частное чисел п и т записывают в виде п : т или п/т, число п называют делимым, а число т - делителем. В множестве Z , как и в множестве N операция деления не всегда выполнима - не для любой пары целых чисел п и т существует их част­ное. Поэтому множество Z (как и N ) не замкнуто относительно операции деле­ния. Однако между операциями деления в множестве N и в множестве Z есть одно существенное различие. В множестве N если частное двух натуральных чисел существует, то оно единственно (см. теорему 8.14). В множестве Z это не так. Если п - произвольное отличное от нуля целое число, а т = 0, то такого числа р, чтобы выполнялось равенство п = т*р не существует; если п = 0 и т = 0, то таких чисел р, для которых выполняется равенство п = т*р существует бес­конечно много. Таким образом, частное от деления целого числа на нуль либо не существует, либо определяется не единственным образом. Поэтому говорят, что делить на нуль нельзя, а выражение 0:0 не определено.

ЗАКОНЫ И СВОЙСТВА АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ НА МНО­ЖЕСТВЕ Z практически полностью совпадают с аналогичными законами и свойствами арифметических операций на множестве Z₀.

СВОЙСТВА МНОЖЕСТВА ЦЕЛЫХ ЧИСЕЛ.СВОЙСТВА МНОЖЕСТВА ЦЕЛЫХ ЧИСЕЛ.

Теорема 8.22. (Теорема Архимеда). Для любых целых чисел а и в существует натуральное число п, что пв> а.

Доказательство. Рассмотрим число п = а', т.е. п = а + 1. В силу теоремы 8.9 и следствия 2 имеем неравенства в > 1 и п > а. Почленно перемножая эти неравенства, получим пв > а. Теорема доказана.

Теорема 8.23. (Принцип наименьшего числа).Любое непустое подмно­жество множества целых чисел содержит наименьшее число.

Доказательство. Пусть множество М таково, что М   и

М  . Рассмотрим два случая.

I. Множество М состоит из конечного числа элементов. В этом случае доказатель­но теоремы проводим методом математической индукции по числу элементов. Если М состоит из одного элемента (М = {а}), то этот элемент и будет наименьшим из чисел, входящих в М. Предположим, что теорема справедлива для множества М, содержащего некоторое конечное число элементов п. Другими словами, считаем, что всякое множество М  , состоящее из п элементов, содержит наименьшее число. Пользуясь предположением, докажем, что множество М  , состоящее из п + 1 элементов, также содержит наимень­шее число. Выберем произвольный  элемент аМ и рассмотрим множество М₁ = М\{а}. Множество М₁ состоит из п элементов, а значит по предположению в нем найдется наименьшее число, которое обозначим через в. Так как а М₁, а в М₁, то а  в, но тогда по теореме 8.10 из двух чисел а и в одно меньше другого. Наименьшее из двух чисел а и в означим через с. Очевидно, что с является наименьшим числом в множестве М.

Итак, все условия метода математической индукции выполнены и справедливость теоремы для любого конечного подмножества доказана.

II. Пусть теперь множество М состоит из бесконечного числа элементов. Выберем любой элемент n из множества М. Число n разбивает множество М на два подмножества:

М₁ = {х/хМ , х  п} и М₂ = {х| хМ х > п }. Множество М₁ состоит из конечного числа элементов (их не более чем п + 1), а значит по первой части теоремы, в нем содержится наименьшее число, которое обозначим через т. Итак, для любого хМ₁ , имеем т  х. В частности, т  п. Но тогда, учитывая определение множества М₂, приходим к выводу, что наименьшее число во всем множестве т . Теорема доказана.

Теорема 8.24. {Принцип наибольшего числа). Если М - непустое под­множество множества целых чисел и существует такое число в, что для любого числа х М выполняется неравенство х <в, то в множе­стве М есть наибольшее число.

Доказательствотеоремы аналогично доказательству теоремы 8.23.

Теорема 8.25. {Свойство дискретности множества Z). Для любого

а Z не существует целого числа п такого, что а < п < а'.

Доказательство проведем методом от противного. Пусть существует такое п, что выполняются оба неравенства: а < п и п < а'. По определению отношения "меньше" существуют такие целые числа с₁ и с₂, такие, что а + с₁ = п и п + с₂= а'. Тогда а + (с₁ + с₂) = а ' т.е. с₁ + с₂ = 1. С другой стороны,

с₁ ≥ 1 и с₂ ≥ 1, поэтому с₁ + с₂ ≥ 2. Пришли к противоречию с допущением, значит, оно неверное. Теорема доказана.

Теорема 8.26. Множество целых чисел Z: а) бесконечное; б) дискретное; в) линейно упорядоченное; г) счетное, д) в нем имеется наименьшее число и нет наибольшего числа; е) в нем выполняются принципы наименьшего и наибольшего числа и свойство Архимеда.

Доказательство, а) В множестве Z есть собственные подмножества, которые ему эквиваленты. Например, множество четных целых чисел является подмножеством Z и ему эквивалентно, поэтому множество Z бесконечное; б) Свойство доказано в теореме 8.25; в) Свойство доказано в теореме 8.10; г) Свойство следует из определения счетного множества: д) Свойство доказано в теореме 8.9 и следствиях нему; е) Свойство доказано в теоремах 8.23 и 8.24.

Теорема 8.35. Множество целых чисел Z: а) бесконечное; б) дискрет­ное; в) линейно упорядоченное; г) счетное, д) в нем нет наибольшего и наименьшего чисел.

Доказательство практически всех свойств аналогично доказательству свойств множества натуральных чисел N и Z₀.

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЦЕЛЫХ ЧИСЕЛ. Каждому целому числу х ставится в соответствие точка М прямой, отстоящая от фиксированной точки 0 на IхI единиц и расположенная на правом луче, если х - положительное число, и на левом, - если х - отрицательное число. Число х, соответствующее точке М, называется координатой этой точки. Тот факт, что точка М имеет координату х, записывается М(х). Изображение целых чисел с помощью точек прямой позволяет задавать не только длины отрезков, но и указывать их направление. Следовательно, геометрически целое число – это направленный отрезок, лежащий на прямой и выходящий из фиксированной точки 0.

Геометрически сложение чисел х и у означает перенос точки М(х) на IуI единиц вправо, если у > 0, и влево, если у < 0. Очевидно, что при у > 0 х + у > х, а при у < 0 х + у < х.