Практикум по высшей математике_часть 2

23)

∫sin4

x

dx ;

2

25)

∫sin3 x dx ;

27)

∫cos7 x dx ;

29)

∫sin6 x dx ;

3

31)

∫cossin

4 xx dx ;

33)

∫tg3 3xdx ;

35)

∫ctg3 xdx ;

37)

∫

dx

;

1 +sin

2 x

39)

∫

dx

;

1

+ tgx

41)

∫

dx

;

sin6 xcos2 x

43)

∫

dx

;

cos6 x

45)

∫

sin xdx

;

1 +sin x

47)

∫

dx

;

3

x

x

sin

cos

3

3

dx

49)

∫

;

(sin x + cos x)2

51)

∫

dx

;

5

−3cos x

6.9. Найти интегралы:

1) ∫

dx

;

x( x + 5 x2

)

3)

∫

dx

;

4

x

x +

2 + 3

x

5) ∫(6 x + 2 3 x + x ) x dx ;

24)

∫sin5 x dx ;

26)

∫cos3 xdx ;

28)

∫(1 + 2cos x)3 dx ;

cos3 x

30)

∫sin2 x dx ;

cos3 x

32)

∫sin4 x dx ;

34)

∫ctg4 2xdx ;

36)

∫

dx

;

1 + cos

2 x

38)

∫

dx

;

3sin2 x +5cos2 x

40)

∫

cos3 xdx

;

sin x

42)

∫

dx

;

sin2 xcos2 x

44)

∫

dx

;

sin4 x

46)

∫

ctg3

x

+ ctg

4 x

dx ;

2

2

48)

∫

dx

;

sin x + cos x

50)

∫

dx

;

5

+ 4sin x

52)

∫

dx

.

sin2 x + tg2 x

2) ∫

x + 3 x2 +

6

x

dx ;

x(1 + 3 x )

4)

∫

xdx

;

3

x

2

−

4

x

6) ∫

x

+

3

x

dx ;

4

5

−

6

7

x

x

99

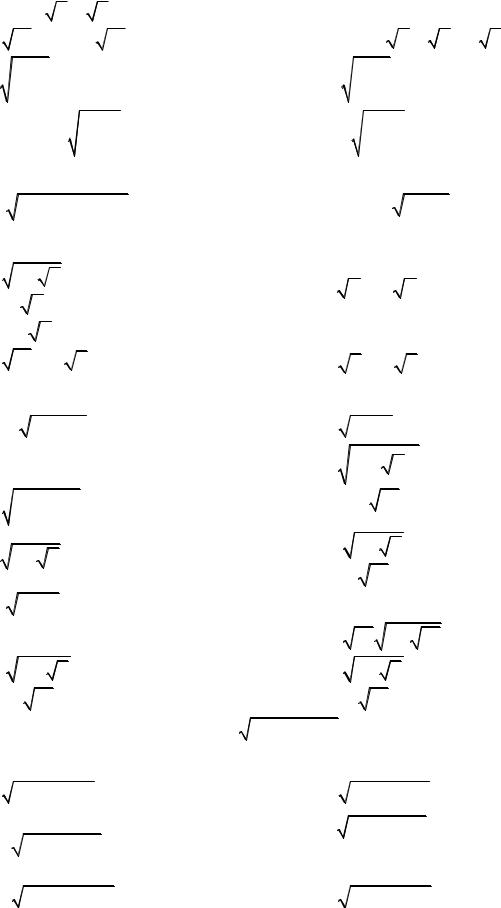
7) ∫

6 −

x + 4

x

dx ;

8) ∫

dx

;

x

3

−

7x −6

4

x

3

x

+

3

x + 2

4

x

9) ∫

1 − x

dx

;

10)

∫

1 + x

dx

;

1 + x

1 − x

1

− x

x

11) ∫

2

2 − x

∫x

2 − x

3

2 + x dx ;

12)

2 + x dx ;

(2 − x)2

13) ∫

dx

;

14)

∫

dx

.

4 (x −1)

3

(2 + x)

5

(2 − x) 4 − x

2

6.10. Найти интегралы от дифференциального бинома:

1)

∫

3 1 + 4

x

dx ;

x

3)

∫

3 xdx

;

x3 (1 −

x )

5)

∫

dx

;

x

2

4 + 2x

2

7)

∫

x3dx

;

3

(

2 + x2 )

2

9)

∫3 1+ 4 xdx ;

11) ∫

3 1+ x3

dx ;

x2

13) ∫

2 +

x

dx ;

4 7

x

6.11. Найти интегралы вида

1)	∫				3x − 2				dx ;
				x	2
						− 2x +8
3)	∫						dx			;
			x	1 −4x − x				2
5)	∫						dx				;
			x		x	2	− 4x +	25

2)

∫ x (1 + 3 x )dx ;

4)

∫

dx

;

x (1 + 3 x )3

6)

∫

x11dx

;

4

1 + x

4 1 +

x

)

3

8)

∫

(

dx ;

x

8

x

7

10) ∫

3 1 +

x

dx ;

3

5

x

12) ∫

dx

;

x3 3 1 + 4

x3

14) ∫

1 +

3

x

dx .

x

3

∫R(x, ax2 +bx + c )dx :

2)

∫

xdx

;

x

2

+ 2x +1

4)

∫ x2 −5x +1dx ;

6)

∫

(2x −1)dx

;

5 − 2x − x

2

100

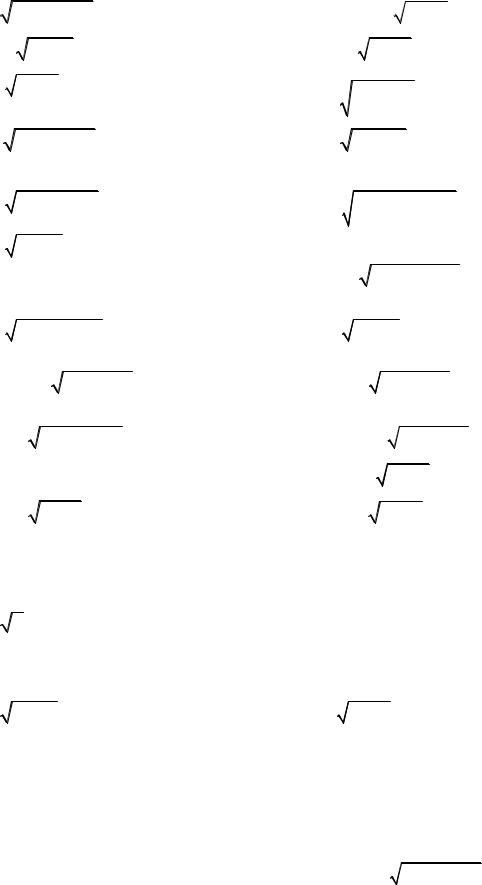
7)

∫

x3dx

;

x

2

− 2x +5

9)

∫x2

4 − x2 dx ;

11)

∫

x2

−1

dx ;

2 +

x2

13)

∫

3 − 2x − x2 dx ;

15)

∫

x4dx

;

x

2

+ 4x +5

17)

∫

x + x2 dx

;

x2

19)

∫

x2dx

;

3x

2

−3x +1

21)

∫

dx

;

(x +1)

1 + x + x

2

23)

∫

dx

;

1

+

x

2

+

4x +

4

25)

∫

dx

;

1

+

1 − x

2

6.12. Найти интегралы:

	∫		x − x3e2 x + x2
1)										dx ;
						x	3
3)	∫		xdx					;
			2
			x	+9
5)	∫		xdx			;
			x −5
7)	∫		dx					;
			x(x +1)
9)	∫					dx			;
			(x +1)(2 −3)

8)

∫

dx

;

(

2

)

2

x

+

1

− x

1

10)

∫x2

x2 −1dx ;

12)

∫

(x2 −1)3 dx ;

14)

∫

9x − x2 dx ;

16)

∫

dx

;

(x2 − 2x +5)

3

18)

∫

(x +1)dx

;

x

2

2x

2

− 2x

+

1

20)

∫

x2dx

;

4 + x

2

22)

∫

dx

;

x

+

x

2

− x +1

24)

∫

dx

;

(x −1)

1 + x − x

2

26)

∫

(x +

1 + x2 )15

dx .

1 + x

2

Разные функции

2)

∫

dx

;

(3x − 4)5

4)

∫

x2dx

;

4 3

1

x +

6)

∫

x +3

dx ;

2x −1

8)

∫

dx

;

x2 −7x +1

10) ∫

dx

;

x

2

−6x +8

101

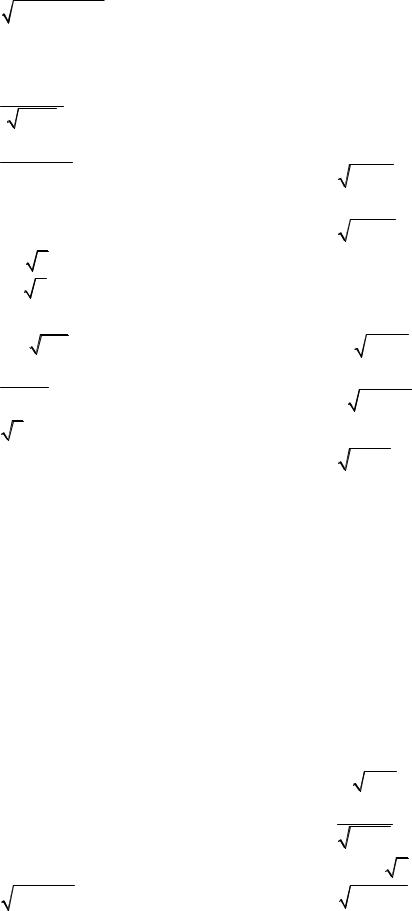
11) ∫		dx		;
	5	− 4x − 4x	2

13) ∫sin 5xsin 7x dx ;

15) ∫sincos3 xdxx ;

17)∫ (x +1)dx ;

x2 + x − 2

19) ∫sin(lnxx)dx ;

21) ∫sin xxdx ;

23)∫(ln x −1)dx ;

xln x

dx

25) ∫e−x −1 ;

	27)	∫		xdx		;
				x −1
	29)	∫(x −1)cos5xdx ;
	31)	∫x 52 x dx ;
	33)	∫x2 cos5xdx ;
	35)	∫x2 e2 xdx ;
	37)	∫		dx						;
				(x −1)(x −2)
	39)	∫		x3dx				;
				x2 +2x −3
	41)	∫earcsin xdx ;
		∫		arcsin ex
	43)			ex		dx ;
	45)	∫		xln	xdx			;
				2	3
				(x	−1)

12)

∫sin 3xcos x dx ;

14)

∫

1 −sin x

dx ;

cos x

16)

∫(x − 4) e4 x2 dx ;

18)

∫

x4dx

;

5

5

x

−

20)

∫ sin5

xdx2

;

cos

x

22)

∫

dx

;

xln2 x

24)

∫

arccos2 xdx

;

1 − x

2

26)

∫

dx

;

x 2x −x

2

28)

∫

e3xdx

;

x

1−e

30)

∫(2x +1)sin 4xdx ;

32)

∫

xcos 2xdx

;

sin3 2x

34)

∫xarccos(2x −1)dx ;

36)

∫e2 x cos 4xdx ;

38)

∫

x2 −2

dx ;

(x +1)(x +

2)

arctgxdx 40) ∫ x4 ;

42)∫ln(x +1)dx ;

x+1

44)∫ x1e+xdxex ;

46) ∫arcsinx(1 − xx) dx .

102

ТЕМА 3

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Понятие определенного интеграла. Формула Ньютона – Лейбница

Пусть функция f (x) , f (x) ≥ 0 определена и ограничена на отрезке [a;b].

Разобьем	произвольно	отрезок	[a;b]	на	n	частей	точками
a = x0 < x1 < x2 <... < xn = b . Из каждого интервала (xi−1 , xi )						возьмем произволь-
ную точку ξi	и составим сумму
	n
	∑ f (ξi )∆xi ,						(6.8)

i=1

где ∆xi = xi − xi−1 .

Сумма (6.8) называется интегральной суммой функции f (x) на отрезке

[a;b]. Предел интегральной суммы при max ∆xi = max (xi − xi−1 )→ 0 , если он
1≤i≤n	1≤i≤n

существует и конечен, называется определенным интегралом от функции f (x) в пределах от a до b и обозначается:

b		n
∫ f (x)dx = maxlim∆x →0 ∑ f (ξi )∆xi .			(6.9)
a	i	i=1
В формуле (6.9)	функция f (x) называется подынтегральной функций;
переменная x – переменной интегрирования; числа a и b			– соответственно
нижним и верхним пределами интегрирования.

Пусть f (x) или непрерывна на отрезке [a;b] или на этом отрезке имеет конечное число точек разрыва первого рода, тогда f (x) интегрируема на этом

отрезке. Для вычисления определенного интеграла используют формулу Нью-

тона – Лейбница

∫b	f (x)dx = F (x)		ba = F (b) − F (a) ,	(6.10)
a

где F(x) – одна из первообразных (любая) функции f (x) .

Свойства определенного интеграла

1. Определенный интеграл зависит только от пределов интегрирования и вида подынтегральной функции и не зависит от обозначения переменной интегрирования, т.е.

103

∫b f (x)dx = ∫b f (t)dt = F (b) − F (a) .

aa

2.При перестановке пределов интегрирования, определенный интеграл меняет знак на противоположный

∫b	f (x)dx = −∫a	f (x)dx .
a	b

3. Определенный интеграл с одинаковыми пределами интегрирования равен нулю

∫a f (x)dx = 0 .

a

4. Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от слагаемых функций

∫b ( f (x) ± g(x))dx = ∫b		f (x)dx ± ∫b g(x)dx .
a	a	a

5. Постоянный множитель (константу) можно выносить за знак определенного интеграла

		∫b	C f (x)dx = C∫b			f (x)dx , где C – произвольная константа.
		a			a
6.	Если c – произвольная точка из [a;b], (c [a;b]), то
		∫b	f (x)dx = ∫c		f (x)dx + ∫b		f (x)dx .
		a		a		c
7.	Знак определенного интеграла:
если		f (x) > 0		для всех x [a;b]				и a < b , то ∫b	f (x)dx > 0 ,
								a
если		f (x) < 0		для всех x [a;b]				и a < b , то ∫b	f (x)dx < 0 .
								a
8.	Если f (x) > g(x)				для всех x [a;b] и a < b , то справедливо неравенство
		∫b	f (x)dx > ∫b g(x)dx .
		a		a

104

9. Если f (x) интегрируема на [a;b] и a < b , то

∫b f (x)dx ≤ ∫b f (x) dx .

aa

10.Если f (x) интегрируема на [a;b], где a < b и для всех x [a;b] справедливы неравенства m ≤ f (x) ≤ M (т.е. функция ограничена на отрезке [a;b]), то

m(b − a)≤ ∫b					f (x)			dx ≤ M (b − a).
			a
11. (Теорема о среднем значении функции.) Если на отрезке [a;b] функ-
ция f (x) непрерывна					и для всех x [a;b] справедливы				неравенства
m ≤ f (x) ≤ M , то найдется x = c , где c [a;b], такое, что
∫b	f (x)dx = (b − a) f (c) .								(6.11)
a
Из формулы (6.11) следует справедливость равенства
ym =		∫b	f (x)dx
		a				.			(6.12)
			b − a
Значение	ym называется средним значением функции f (x)								на отрезке
[a;b].

Определенный интеграл как функция верхнего предела

Если функция интегрируема на отрезке [a;b], то она интегрируема и на отрезке [a; x], где x [a;b]. Если верхний (или нижний) предел интегрирова-

ния принимает различные значения, то интеграл становиться функцией от верхнего (нижнего) предела интегрирования. Обозначим верхний предел через

x , а переменную интегрирования через t		в отличие от верхнего предела. Тогда
на отрезке [a;b] определена функция от переменной x вида
Φ(x) = ∫x	f (t)dt .	(6.13)
a

Функция (6.13) называется интегралом с переменным верхним пределом интегрирования.

105

Если f (x) − непрерывная функция и Φ(x) = ∫x f (t)dt , то имеет место ра-

a

венство Φ′(x) = f (x) . Данное равенство означает, что для непрерывной на от-

резке [a;b] функции f (x) интеграл Φ(x) = ∫x	f (t)dt является первообразной
a
функцией.

Формулы замены переменной и интегрирования по частям в определенном интеграле

Пусть функция f (x) интегрируема на отрезке [a;b]. Введем новую переменную интегрирования x =ϕ(t) , где ϕ(t) – однозначна, непрерывна и имеет

	′
непрерывную производную ϕ (t) на отрезке [α; β], причем ϕ(α) = a , ϕ(β) = b .
Тогда справедлива формула замены переменной в определенном интеграле
b	β

	′
∫ f (x)dx = ∫ f (ϕ(t))ϕ (t)dt .
a	α

На практике замену переменной проводят с помощью монотонных непрерывно дифференцируемых функций. При этом замену пределов интегрирования удобно записывать в виде таблицы

x	a	b
			.
t	α	β

Пусть функции u(x) и v(x) дифференцируемы на отрезке [a;b]. Тогда справедлива формула интегрирования по частям в определенном интеграле

b b

∫udv = uv ba − ∫vdu .

a a

Приближенное вычисление определенных интегралов

1. Формула прямоугольника. Отрезок [a;b] разбивают на n равных час-

тей точками	x	= a +	b − a	k ,	k = 0,1,..., n . Тогда определенный интеграл от не-
	k		n
прерывной на [a;b] функции f (x) приближенно равен
	b			n−1	n
	∫ f (x) ≈ b − a ∑ f (xk ) =b − a ∑ f (xk ) .
	a		n k =0		n k =1

106

2.

Формула трапеции.

b

b

− a f (a) +

f (b)

n−1

∫ f (x) ≈

∑ f (xk )

n

+

,

2

a

k =0

где

x

= a +

b − a

k ,

k = 0,1,..., n −1.

k

n

3.

Формула Симпсона. Отрезок [a;b] разбивают на 2n равных частей

b

b

− a

n

n−1

∫ f (x) ≈

,

6n

f (a) + f (b) + 2∑ f (x2k ) + 4∑ f (x2k −1 )

a

k =1

k =1

где

x

= a +

b − a

k ,

k = 0,1,...,2n .

k

2n

Примеры решения задач

Пример 6.40. Вычислить ∫3

x3dx .

1

Решение. Так как одной из первообразных для

функции

x3 является

функция

x4

, то, применяя формулу Ньютона - Лейбница, находим

4

3

x

4

3

4

4

∫x3dx =

= 3

−1

= 81 −1

= 20 .

1

4

1

4

4

4

Пример 6.41. Вычислить интегралы:

π

2) ∫1

dx

3) ∫3

dx

1)

∫2 sin 2xdx ;

;

.

2

0

0 1 + x

1 1 + x

Решение. Используя таблицу интегралов и формулу Ньютона – Лейбница,

получаем:

π

π 2

1)

∫2 sin 2xdx = −cos 2x

= −1 (cosπ −cos0)= −

1 (−1 −1)=1;

0

2

0

2

2

1

dx

1

π

π

2) ∫0

= arctg x

= arctg1 −arctg 0 = 4 −0 =

4

;

1 + x2

0

107

3) ∫3	dx	= ln |1 + x |		13 = ln 4 −ln 2 = ln	4	= ln 2 .
	1 + x				2
1

Замечание: Формула Ньютона – Лейбница может быть использована только для вычисления определенного интеграла от непрерывной на отрезке [a;b] функции f (x) , если равенство F′(x) = f (x) справедливо на всем отрезке

[a;b]. Если в качестве первообразной использовать разрывную функцию, то может быть получен неверный результат (см. пример 6.48).

	π
Пример 6.42. Вычислить ∫2 cos x esin xdx .
	1
Решение. Используем подстановку
t =sin x;	x			0			π	2	.
dt = cos xdx;
	t			0		1

На отрезке [0; 1] функция x = arcsin t является монотонной, следователь-

но, можно использовать приведенную замену переменной. Тогда

π

1

∫2 cos x esin xdx = ∫1 et dt = et

= e1 −e0 = e −1.

0

0

0

π

Пример 6.43. Вычислить ∫2 xsin xdx .

Решение.

0

π

u

= x,

dv = sin xdx

π

∫2 xsin xdx =

= −xcos x

π0

2

+ ∫2 cos xdx =

0

du = dx, v = −cos x

0

= π cos π +sin x

π 2 = sin π

−sin 0 =1.

2

2

0

2

Пример 6.44. Определить среднее значение функции y =sin x на отрезке

[0; π].

Решение. Согласно формуле (6.12), получаем

ym =	π∫sin xdx	= −	1	cos x		π0	= −	1	(cosπ −cos0)=	2	.
	0
	π −0		π					π		π

108